5.1认识一元一次方程课件

课件36张PPT。牡丹区实验中学5.1认识一元一次方程 知识回顾1 、 什么叫方程？2 、什么叫方程的解？使方程两边相等的未知数的值叫做方程的解含有未知数的等式叫做方程 破冰游戏一、说出二、同位两个合作：分别用以上规则猜对方爸爸或妈妈的年龄。逆向
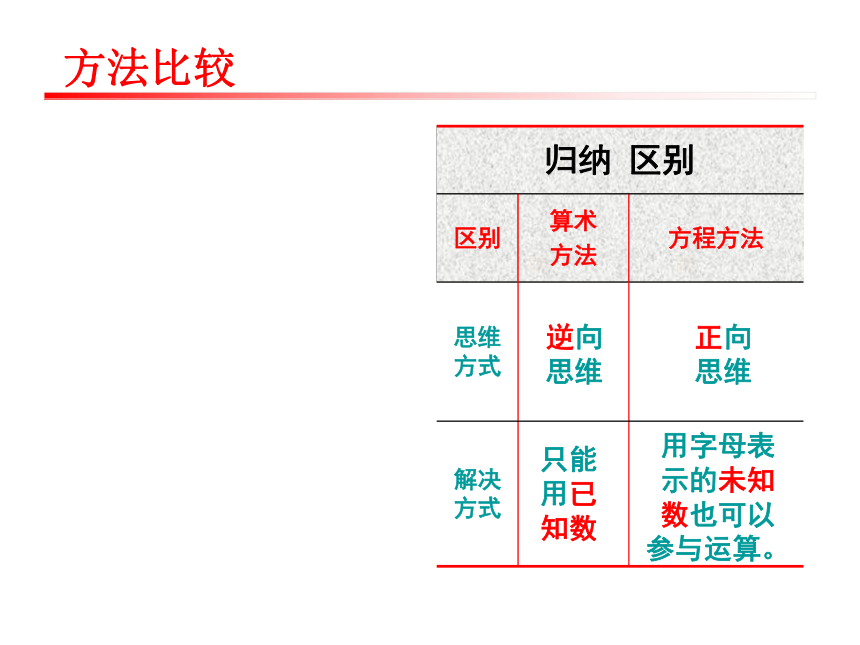
思维正向
思维只能用已知数用字母表示的未知数也可以参与运算。 方法比较“曹州牡丹园”建于1982年，面积1600亩，（约1000000平方米）是目前世界上品种最多，面积最大的牡丹园，集中了曹州牡丹传古至今的发展成果，如果长和宽之差为 500m，牡丹园的长与宽分别是多米？如果设这个牡丹园的宽为x m，那么长为 __________m，
用x表示牡丹园的面积为________
可以得到方程:
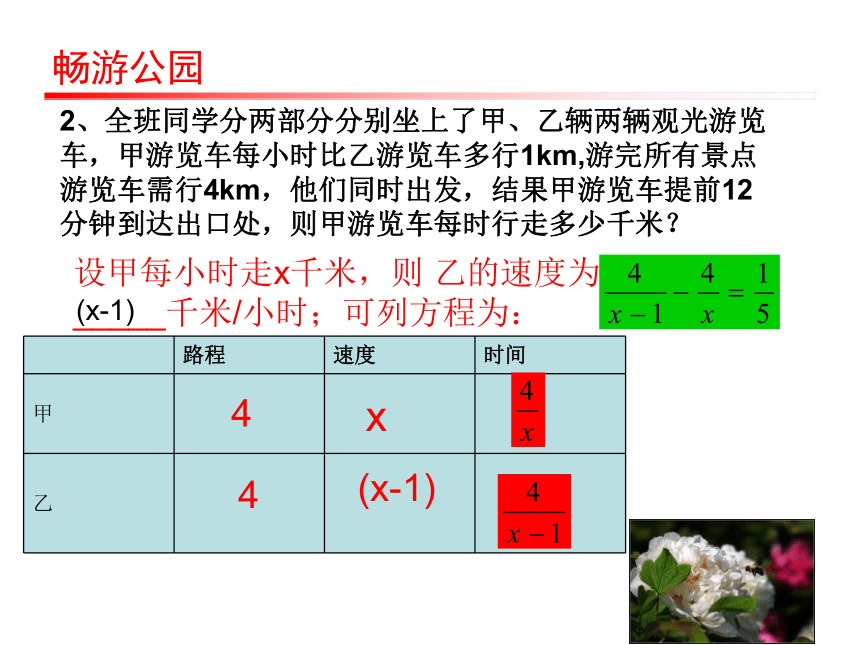
分析x2+500x=1000000畅游公园两位老师带某班全体同学去牡丹园游玩，成人票60元，学生半票，共花费1260元，这个班的学生共多少人？设这个班的学生共x人，则学生买票的钱数为_____,老师买票的钱数为________.可列方程：30x60x2畅游公园2、全班同学分两部分分别坐上了甲、乙辆两辆观光游览车，甲游览车每小时比乙游览车多行1km,游完所有景点游览车需行4km，他们同时出发，结果甲游览车提前12分钟到达出口处，则甲游览车每时行走多少千米？
设甲每小时走x千米，则 乙的速度为_____千米/小时；可列方程为：(x-1)44x(x-1)畅游公园3、今年牡丹花期，曹州牡丹园游客量和经济收入均创历史新高。票务收入首次突破1000万元、比去年增长20%，那么去年票收入为多少万元？如果设去年票收入为x万元，那么可以得到方程：（1+20%）x=1000 畅游公园知识点拨1）由上面的问题你得到了哪些方程？其中哪些是你熟悉的方程？
2）方程 有什么共同特点？细心观察（1）x2+500x=1000000（4）（1+20%）x=1000 （4）（1+20%）x=1000 识记概念　只含有一个未知数（元），并且未知数的指数是1（次）的方程叫做一元一次方程．定义
例1、已知是 关于x一元一次方程，则a的值为


2变式训练怎么判断 一个方程是一元一次方程？ ①只含有一个未知数；

②并且未知数的指数是1 。
③方程左右两边必须是整式
特别需要注意的地方：1、分母不能够含未知数
2、化简之后再判断
识记概念练习　判断下列式子是不是一元一次方程，为什么？
(1) 2x-1=0
(2) 5x+2
(3) 2x2-4x=5
(4) 2y+3=-6
(5) x-7y=5
(6) 2y-3=9
辨别真假如果 是关于x一元一次方程，那么 =
-1变式训练1、4×（ ）=24
2、2 ×（ ）-1=5　　
　　像这样，能使方程左右两边的值相等的未知数的值，
叫做方程的解　　
如：方程 1、4x=24 ，2、2x-1=5
当x为何值时，等号左右两边相等？　　
通过观察可知：1、当x=6时；2、当x=3时：类比记忆
1、代值；2、计算；3、判断左边值是否等于右边的值。判断是否为方程的解的方法步骤：是不是
是下列方程的解吗？
（1）
（2）
类比记忆
百花争艳
动脑筋 墓中
长眠着一位伟大的人物
－丢番图！
他一生六分之一的时光，
是童年时代；
又度过了十二分之一的岁月之后，
他满脸长出了胡须；
再过了七分之一的年月时，
举行了花烛庆典；
婚后五年，
得一贵子。
可是不幸的孩子，
他仅仅活了他父亲的半生时光，
就离开了人间。
从此，作为父亲的丢番图，
在悲伤中度过四年之后，
结束了自己的一生。
下列方程中，解为-2的是（ ）C在下列方程中：
①2χ=3; ②y2-1=2y ③2x+y=-3; ④6m-2=0; ⑤8x+5y=1
属于一元一次方程的是 。
方程2xa+1+ 3=0是一元一次方程，
则代数式 -5a+6= 。
畅谈收获4、某长方形操场的面积是 5 850，长和宽之差
为 25 m，这个操场的长与宽分别是多米？如果设这个操场的宽为 x m，那么长为 m，可以得到方程:x2+25x=5805（x+25 ）列方程畅游公园列方程1、小颖种了一株树苗，开始时树苗高为40厘米，栽种后每周升高约5厘米，大约几周后树苗长高到1米？

2、甲、乙两地相距22km,张叔叔从甲地出发到乙地，每时比原计划多行走1km,因此提前12分钟到达乙地，张叔叔原计划每时行走多少千米？
如果设x周后树苗长高到1米，那么可以得到方程：设张叔叔原计划每时行走xkm,可以得到方程：?在我国，“方程”一词最早出现于 《九章算术》．它共分九章，第八章就叫“方程”.
? 12世纪前后，我国数学家用 “天元术”来解题，即先要“立天元为某某”，相当于“设X为某某”．
? 14世纪初，我国元朝数学家朱世杰创立了“四元术”，四元指天、地、人、物，相当于四个未知数．品渊源中国古代数学家在方程发展过程中所做贡献１、在下列方程中：
①2χ=3; ②y2-1=2y ③2x+y=-3; ④6m-2=0; ⑤8x+5y=1
属于一元一次方程的是 。
2、方程2xa+1+ 3=0是一元一次方程，则代数式 -5a+6= 。
3、方程(m-2)x+5x-1=0是关于x的一元一次方程，则m= 。
4、根据条件列方程。
1）某数χ的相反数比它的 大1。

2）某数a的4倍等于某数的3倍与7的差．

3）把某数y增加20%后比这数的80%大5．
测达标
5、根据题意，列出方程：
1）、在一卷公元前1600年左右遗留下来的古埃及草卷中，记载着一些数学问题。其中一个问题翻译过来是：“啊哈，它的全部，它的 ，其和等于19。” 你能求出问题中的“它”吗？



2）、甲、乙两队开展足球对抗赛，规定每队胜一场得3分，平一场得1分，负一场得0分。甲队与乙队一共比赛了10场，甲队保持了不败记录，一共得了22 分，甲队胜了多少场？平了多少场？

谈收获归纳:
? 方程、一元一次方程的概念　　实际问题一元一次方程 分析实际问题中的数量关系，利用其中的相等关系列出方程，是用数学解决实际问题的一种方法。 设未知数 列方程(1) 阅读教材相关内容，然后完成教材第76 页的习题6、7、8.
(2) 选做作业：
设计一道以“2008北京奥运会”为实际背景的可列出一元一次方程的应用题。
要求：
设计一个符合2008北京奥运会的情境；
所编应用题完整，题意清楚. 布置作业发现问题：下列方程哪些是一类的？为什么？
　　　　　　(1) 2 -1=0
(2) 25 -1=124
(3) 2[ +( -25)] =310
(4) 2 +3=-6
观察发现1、2、3、4题
都含有1个未知数且未
知数的指数都是1(5)X+y=5
(6)x2-36=8xxxxy11111
欢 迎 指 教

谢 谢 大 家欢迎指教
谢谢大家练习　列方程研究古代问题：
巍巍古寺在山林，不知寺内几多僧。
三百六十四只碗，看看用尽不差争。
三人共食一碗饭，四人共吃一碗羹。
请问先生明算着，算来寺内几多僧。
相等关系: 饭碗数 + 汤碗数 = 364
用 X表示寺内的和尚人数，根据题意，得到方程4.4 .2 回顾举例 定义方程