人教A版(2019)高中数学选择性必修第一册 《空间向量及其运算》专题精讲课件(共26张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 《空间向量及其运算》专题精讲课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 15:40:53 | ||
图片预览








文档简介
(共26张PPT)
人教A版同步教材名师课件
空间向量及其运算
---专题精讲
空间向量的相关概念
(1)空间向量的定义
在空间中,我们把具有大小和方向的量叫做向量.
与平面向量一样,空间向量也用有向线段表示,记作:或.
(2)空间向量的有关概念
零向量:长度为0或者说起点和终点重合的向量,记为0.
规定:0与任意向量平行.
单位向量:长度为1的空间向量,即.
相等向量:方向相同且模相等的向量.
相反向量:方向相反但模相等的向量.
空间向量的相关概念
共线向量:如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量.平行于记作.当我们说向量共线(或)时,表示的有向线段所在的直线可能是同一直线,也可能是平行直线.
共面向量:平行于同一个平面的向量,叫做共面向量.
向量在空间中是可以平移的.空间任意两个向量都可以平移到同一个平面内,因此我们说空间任意两个向量是共面的.
空间向量的相关概念
(3)空间向量的长度(模)
表示空间向量的有向线段的长度叫做向量的长度或模,记作或,在空间两个向量的数量积中,特别地,所以向量的模:.
将其推广:.
典例1 下列关于空间向量的说法中正确的是( )
A.方向相反的两个向量是相反向量
B.空间中任意两个单位向量必相等
C.若向量满足,则
D.相等向量其方向必相同
典型例题
解析
本题考查空间向量的相关概念,在理解相反向量、相等向量的定义概念,以及空间向量的概念的基础之上可以判断出正确选项.
A中,方向相反,长度相等的两个向量是相反向量;B中,单位向量模都相等而方向不确定;C中,向量作为矢量不能比较大小.
D
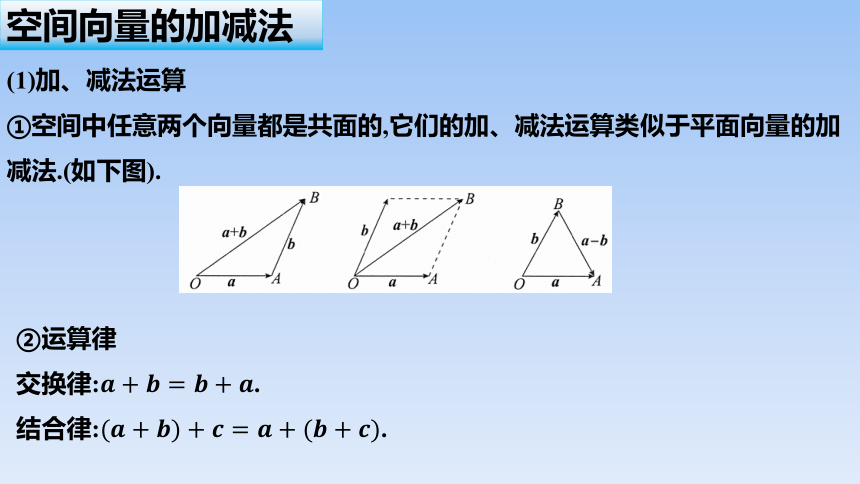
空间向量的加减法
(1)加、减法运算
①空间中任意两个向量都是共面的,它们的加、减法运算类似于平面向量的加减法.(如下图).
②运算律
交换律:.
结合律:.
空间向量的加减法
(2)数乘运算
①定义:实数与空间向量的乘积仍是一个向量,称为向量的数乘运算.
当时,与方向相同;当时,与方向相反.的长度是的长度的倍.当时,.
②运算律
分配律:.
结合律:.
典例2 如图,空间四边形中,,,点在线段上,且,点为的中点,则( )
A. B.
C. D.
典型例题
解析
本题通过空间四边形考查向量的加、减运算,利用向量运算的平行四边形法则和三角形法则,可以分析计算得到正确答案.
典例2 如图,空间四边形中,,,点在线段上,且,点为的中点,则( )
A. B.
C. D.
典型例题
解析
∵.
A
共线定理
(1)共线向量的定义
与平面向量一样,如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量,记作.
注意:0与任意向量是共线向量.
(2)共线向量定理
空间任意两个向量的充要条件是存在实数,使.
(3)共线向量定理扩展
此定理可分解为以下两个命题:
①存在唯一实数,使得.
②存在唯一实数,使得,则.
注意:不可丢掉,否则实数就不唯一.
(4)共线向量定理的用途.
①判定两条直线平行(进而证线面平行).
②证明三点共线.
共线定理
典型例题
解析
证明:∵分别为的中点,∴, ,同理, .从而四边形为平行四边形,对角线相交于一点,且为它们的中点.连接.
只要能证明向量,就可以说明三点共线,且为的中点.事实上,,,而为的中点,
典例3 证明:在四面体中连接对棱中点的三条直线交于一点且互相平分.(此点称为四面体的重心)
思路
本题考查共线向量的相关证明,根据向量共线的充要条件,在几何图形的基础上可以推测出相关向量的关系,进而说明论证.
典型例题
解析
.
∴经过点,且为的中点.
即证得、、相交于点为它们的中点,原命题得证.
典例3 证明:在四面体中连接对棱中点的三条直线交于一点且互相平分.(此点称为四面体的重心)
共面定理
(1)共面向量的定义
通常把平行于同一平面的向量,叫做共面向量.
注意:空间任意两个向量是共面的,但空间任三个向量就不一定共面了.
(2)共面向量定理
如果两个向量不共线,与向量共面的充要条件是存在唯一的有序实数对,使.
共面定理
推论:空间一点位于平面内的充分必要条件是存在有序实数对,使或对空间任一点,有,上式叫做平面的向量表达式.
(3)共面向量定理的用途
①证明四点共面.②线面平行(进而证面面平行).
典型例题
解析
证明:(1)∵四边形是平行四边形,∴,
,∴共面.
(2)∵,
又∵,所以,平面平面.
典例4 已知,从平面外一点引向量.(1)求证:四点共面;(2)求证:平面平面.
思路
本题考查向量共面的充要条件,根据所给条件,对共面向量进行推理论证,根据数量关系进行分析计算.
空间向量的数量积
(1)两个向量的数量积
已知两个非零向量,则叫做向量与的数量积,记作,即.
(2)空间向量数量积的性质
设是非零向量,是单位向量,则
①.②.
③或.④.
⑤.
空间向量的数量积
(3)空间向量的数量积满足如下运算律
①.②(交换律).
③(分配律).
(4)空间向量的数量积有关注意事项
①对于三个不为0的实数,若,则;对于三个不为0的向量,若不能得出,即向量不能约分.
②若,不能得出(或),就是说,向量不能进行除法运算.
③对于三个不为0的实数,有,对于三个不为0的向量,有,向量的数量积不满足结合律.
典型例题
解析
∵向量,向量与的夹角都是,且,
∴.
(1);
(2).
典例5 已知向量,向量与的夹角都是,且.试求:(1);(2).
思路
本题考查空间向量的数量积运算,根据所给向量模的长度以及向量间的夹角,利用数量积公式,可以分析计算出所求式子的结果.
空间两个向量的夹角
(1)定义及相关概念
①已知两个非零向量,在空间任取一点,作,则叫做向量与的夹角,记作,如下图.
根据空间两个向量数量积的定义:,
那么空间两个向量的夹角的余弦值.
②规定:,特别地,如果,那么与同向;如果,那么与反向.如果,那么与垂直,记作.
空间两个向量的夹角
(2)利用空间向量求异面直线所成的角
异面直线所成的角可以通过选取直线的方向向量,计算两个方向向量的夹角得到.
在求异面直线所成的角时,应注意异面直线所成的角与向量夹角的区别:如果两向量夹角为锐角或直角,则异面直线所成的角等于两向量的夹角;如果两向量的夹角为钝角,则异面直线所成的角为两向量的夹角的补角.
典型例题
解析
设,则,且、、三个向量两两夹角均为,.故所成角的余弦值为.
典例6 如图所示,已知是边长为1的正三角形所在平面外一点,且分别是的中点,求异面直线与所成角的余弦值.
思路
本题考查异面直线之间所成角的问题,在理解求角公式的基础上,通过分析计算可求得异面直线和所成角的余弦值.
空间向量的垂直
若,则称与互相垂直,并记作.根据数量积的定义:.
典型例题
典例7 如图,已知空间四边形的各边和对角线的长都等于,点分别是的中点.
(1)求证:;(2)求的长.
思路
本题考查空间向量数量积的应用,第一问判断垂直的位置关系,根据点分别是的中点,可利用边长表示向量,再通过数量积公式,得到数量积为0,即可推理判断出垂直的位置关系;第二问求线段长度,可利用向量求模公式进行分析计算.
典型例题
解析
(1)设.由题意可知:,且三向量两两夹角均为.∴,同理可证.
典例7 如图,已知空间四边形的各边和对角线的长都等于,点分别是的中点.
(1)求证:;(2)求的长.
典型例题
解析
典例7 如图,已知空间四边形的各边和对角线的长都等于,点分别是的中点.
(1)求证:;(2)求的长.
(2)由(1)可知.
的长为.
人教A版同步教材名师课件
空间向量及其运算
---专题精讲
空间向量的相关概念
(1)空间向量的定义
在空间中,我们把具有大小和方向的量叫做向量.
与平面向量一样,空间向量也用有向线段表示,记作:或.
(2)空间向量的有关概念
零向量:长度为0或者说起点和终点重合的向量,记为0.
规定:0与任意向量平行.
单位向量:长度为1的空间向量,即.
相等向量:方向相同且模相等的向量.
相反向量:方向相反但模相等的向量.
空间向量的相关概念
共线向量:如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量.平行于记作.当我们说向量共线(或)时,表示的有向线段所在的直线可能是同一直线,也可能是平行直线.
共面向量:平行于同一个平面的向量,叫做共面向量.
向量在空间中是可以平移的.空间任意两个向量都可以平移到同一个平面内,因此我们说空间任意两个向量是共面的.
空间向量的相关概念
(3)空间向量的长度(模)
表示空间向量的有向线段的长度叫做向量的长度或模,记作或,在空间两个向量的数量积中,特别地,所以向量的模:.
将其推广:.
典例1 下列关于空间向量的说法中正确的是( )
A.方向相反的两个向量是相反向量
B.空间中任意两个单位向量必相等
C.若向量满足,则
D.相等向量其方向必相同
典型例题
解析
本题考查空间向量的相关概念,在理解相反向量、相等向量的定义概念,以及空间向量的概念的基础之上可以判断出正确选项.
A中,方向相反,长度相等的两个向量是相反向量;B中,单位向量模都相等而方向不确定;C中,向量作为矢量不能比较大小.
D
空间向量的加减法
(1)加、减法运算
①空间中任意两个向量都是共面的,它们的加、减法运算类似于平面向量的加减法.(如下图).
②运算律
交换律:.
结合律:.
空间向量的加减法
(2)数乘运算
①定义:实数与空间向量的乘积仍是一个向量,称为向量的数乘运算.
当时,与方向相同;当时,与方向相反.的长度是的长度的倍.当时,.
②运算律
分配律:.
结合律:.
典例2 如图,空间四边形中,,,点在线段上,且,点为的中点,则( )
A. B.
C. D.
典型例题
解析
本题通过空间四边形考查向量的加、减运算,利用向量运算的平行四边形法则和三角形法则,可以分析计算得到正确答案.
典例2 如图,空间四边形中,,,点在线段上,且,点为的中点,则( )
A. B.
C. D.
典型例题
解析
∵.
A
共线定理
(1)共线向量的定义
与平面向量一样,如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量,记作.
注意:0与任意向量是共线向量.
(2)共线向量定理
空间任意两个向量的充要条件是存在实数,使.
(3)共线向量定理扩展
此定理可分解为以下两个命题:
①存在唯一实数,使得.
②存在唯一实数,使得,则.
注意:不可丢掉,否则实数就不唯一.
(4)共线向量定理的用途.
①判定两条直线平行(进而证线面平行).
②证明三点共线.
共线定理
典型例题
解析
证明:∵分别为的中点,∴, ,同理, .从而四边形为平行四边形,对角线相交于一点,且为它们的中点.连接.
只要能证明向量,就可以说明三点共线,且为的中点.事实上,,,而为的中点,
典例3 证明:在四面体中连接对棱中点的三条直线交于一点且互相平分.(此点称为四面体的重心)
思路
本题考查共线向量的相关证明,根据向量共线的充要条件,在几何图形的基础上可以推测出相关向量的关系,进而说明论证.
典型例题
解析
.
∴经过点,且为的中点.
即证得、、相交于点为它们的中点,原命题得证.
典例3 证明:在四面体中连接对棱中点的三条直线交于一点且互相平分.(此点称为四面体的重心)
共面定理
(1)共面向量的定义
通常把平行于同一平面的向量,叫做共面向量.
注意:空间任意两个向量是共面的,但空间任三个向量就不一定共面了.
(2)共面向量定理
如果两个向量不共线,与向量共面的充要条件是存在唯一的有序实数对,使.
共面定理
推论:空间一点位于平面内的充分必要条件是存在有序实数对,使或对空间任一点,有,上式叫做平面的向量表达式.
(3)共面向量定理的用途
①证明四点共面.②线面平行(进而证面面平行).
典型例题
解析
证明:(1)∵四边形是平行四边形,∴,
,∴共面.
(2)∵,
又∵,所以,平面平面.
典例4 已知,从平面外一点引向量.(1)求证:四点共面;(2)求证:平面平面.
思路
本题考查向量共面的充要条件,根据所给条件,对共面向量进行推理论证,根据数量关系进行分析计算.
空间向量的数量积
(1)两个向量的数量积
已知两个非零向量,则叫做向量与的数量积,记作,即.
(2)空间向量数量积的性质
设是非零向量,是单位向量,则
①.②.
③或.④.
⑤.
空间向量的数量积
(3)空间向量的数量积满足如下运算律
①.②(交换律).
③(分配律).
(4)空间向量的数量积有关注意事项
①对于三个不为0的实数,若,则;对于三个不为0的向量,若不能得出,即向量不能约分.
②若,不能得出(或),就是说,向量不能进行除法运算.
③对于三个不为0的实数,有,对于三个不为0的向量,有,向量的数量积不满足结合律.
典型例题
解析
∵向量,向量与的夹角都是,且,
∴.
(1);
(2).
典例5 已知向量,向量与的夹角都是,且.试求:(1);(2).
思路
本题考查空间向量的数量积运算,根据所给向量模的长度以及向量间的夹角,利用数量积公式,可以分析计算出所求式子的结果.
空间两个向量的夹角
(1)定义及相关概念
①已知两个非零向量,在空间任取一点,作,则叫做向量与的夹角,记作,如下图.
根据空间两个向量数量积的定义:,
那么空间两个向量的夹角的余弦值.
②规定:,特别地,如果,那么与同向;如果,那么与反向.如果,那么与垂直,记作.
空间两个向量的夹角
(2)利用空间向量求异面直线所成的角
异面直线所成的角可以通过选取直线的方向向量,计算两个方向向量的夹角得到.
在求异面直线所成的角时,应注意异面直线所成的角与向量夹角的区别:如果两向量夹角为锐角或直角,则异面直线所成的角等于两向量的夹角;如果两向量的夹角为钝角,则异面直线所成的角为两向量的夹角的补角.
典型例题
解析
设,则,且、、三个向量两两夹角均为,.故所成角的余弦值为.
典例6 如图所示,已知是边长为1的正三角形所在平面外一点,且分别是的中点,求异面直线与所成角的余弦值.
思路
本题考查异面直线之间所成角的问题,在理解求角公式的基础上,通过分析计算可求得异面直线和所成角的余弦值.
空间向量的垂直
若,则称与互相垂直,并记作.根据数量积的定义:.
典型例题
典例7 如图,已知空间四边形的各边和对角线的长都等于,点分别是的中点.
(1)求证:;(2)求的长.
思路
本题考查空间向量数量积的应用,第一问判断垂直的位置关系,根据点分别是的中点,可利用边长表示向量,再通过数量积公式,得到数量积为0,即可推理判断出垂直的位置关系;第二问求线段长度,可利用向量求模公式进行分析计算.
典型例题
解析
(1)设.由题意可知:,且三向量两两夹角均为.∴,同理可证.
典例7 如图,已知空间四边形的各边和对角线的长都等于,点分别是的中点.
(1)求证:;(2)求的长.
典型例题
解析
典例7 如图,已知空间四边形的各边和对角线的长都等于,点分别是的中点.
(1)求证:;(2)求的长.
(2)由(1)可知.
的长为.
