人教A版(2019)高中数学选择性必修第一册 《空间向量与立体几何---名校新题聚焦》名师课件(共21张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 《空间向量与立体几何---名校新题聚焦》名师课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 15:41:50 | ||
图片预览








文档简介
(共21张PPT)
《空间向量与立体几何》
人教A版同步教材名师课件
---名校新题聚焦
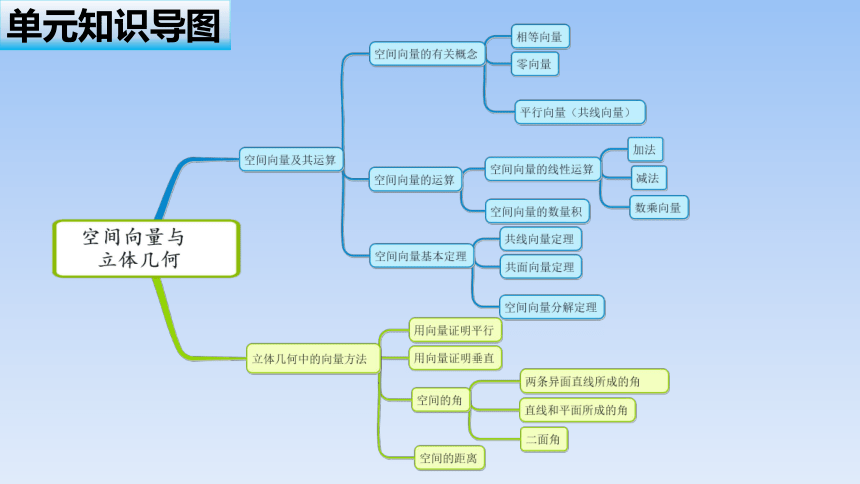
单元知识导图
1.2020.人民大学附属中学质量检测
某棱锥的三视图如图所示,则该棱雉的外接球的表面积为 ( )
A. B. C. D.
名校新题聚焦
学审题(1)三视图对应的几何体是什么图形
(2)求解几何体外接球问题有哪些方法 该几何体的外接球问题运用几何法易求解吗
(3)若运用代数方法该如何求解
解析
如图,在长、宽、高分别为2,1,1的长方体中,所在棱的中点,由三视图的知识可知,几何体即三棱锥,以为坐标原点建立空间直角坐标系.
A
如图所示,则,设外接球的球心为,半径为,则,于是有解得所以,所以外接球的半径为,表面积为.故选A.
用坐标法求解,要善于借助长方体.将几何体纳入长方体后,各个顶点的坐标容易求出,设出球心坐标,利用球心到球面上各顶点的距离都等于半径,求得球心坐标,进而求得面积.
名校新题聚焦
名师综评
2.2020 长沙长郡中学月考
如图,甲站在水库底面上的点处,乙站在水坝斜面上的点处,已知测得从D,C到库底与水坝的交线的距离分别为的长为 ,CD的长为 则库底与水坝所成的二面角的大小为______.
名校新题聚焦
学审题(1)此题要求什么 易直接求解吗
(2)求二面角的平面角有哪些方法 此题宜采用何种方法
(3)条件中有哪些线段长度已知,它们的位置关系是什么
解析
,
,
.
又,
,
解得,
库底与水坝所成的二面角,故答案为.
本题解题的关键是通过对实际问题的抽象,建立数学模型,进而从向量的角度快速解决.
名校新题聚焦
名师综评
名校新题聚焦
解析
以为坐标原点,射线分别为轴的正方向建立空间直角坐标系(图略),所以球心,故到直线的距离为,而球的半径为,所以在球内的线段长度为.故选A .
3.2020.成都第七中学月考
棱长为1的正方体内有一个内切球,过正方体中两条互为异面直线的的中点作直线,该直线被球面截在球内的线段的长为( )
A. B. C. D.
学审题 (1)正方体内切球半径是多少
(2)要求直线被内切球面截得的线段长,先应求出什么
(3)解决此题有哪些方法可考虑
A
本题的解题关键是求出球心到直线的距离,既可用几何方法也可用坐标法.
名师综评
名校新题聚焦
解析
由题意知内切球的半径为1,设球心为,
则.
.
4.2020·上海中学期末检测
点是底面边长为,高为2的正三棱柱表面上的动点,是该棱柱内切球的一条直径,则的取值范围是_______.
学审题 (1)题中点什么点 有什么特殊性
(2)正三棱柱的内切球半径等于多少
(3)直接求容易吗 需要如何处理
求两向量数量积的常用方法:
(1)直接求,运用求解.
(2)坐标法,运用求解,,.
(3)若直接求较困难,可把转化为其他模与夹角易求的向量再求解.
名师综评
名校新题聚焦
解析
以为坐标原点,建立如图所示的空间直角坐标系,则,
5.2020 河北衡水中学质量检测
如图,在四棱柱中,平面,底面是边长为的正方形,侧棱的长为为侧棱上的动点(包括端点),则( )
A.对任意的,存在点,使得
B.当且仅当,存在点,使得
C.当且仅当,存在点,使得
D.当且仅当,存在点,使得
学审题 (1)图中哪些点是定点,哪些点是动点 (2)如果运用坐标法,该如何表示坐标
(3)由能得到什么结论 (4)如何确定存在所满足的条件
设,则,
所以,令,则,由得,
所以当且仅当时,存在点,使得
B
名师综评
本题也可用三垂线定理,在平面内,探求成立所满足的条件.
名校新题聚焦
解析
以为坐标原点, ,分别以所在的直线为x轴、y轴、z轴,建立空间直角坐标系(图略).
则,设,因为,所以,
所以,
又,
由可得,所以,故线段的长度的最大值为6.
6.2020.华师一附中阶段检测
在长方体中,已知底面为正方形,为的中点,,点是正方形所在平面内的一个动点,且,则线段的长度的最大值为( )
A.8 B.10 C.6 D.12
学审题 (1)解答本题的关键是确定动点Q运动的轨迹,点Q满足什么条件?
(2)确定点Q的轨迹,最好是采用几何法,还是坐标法?
(3)若用坐标法,点Q的坐标如何设?
(4)点Q在什么位置时,线段BQ的长度最大?
C
立体几何中的动点的轨迹确定,解答时通常要根据几何体在相关线段、平面的变化规律,洞悉其变化特点,哪些点、线保持不变,哪些点、线在变化,是按什么规律变化的,进而可将动态固定下来考虑.
名校新题聚焦
名师综评
名校新题聚焦
解析
以为坐标原点, ,分别以所在的直线为x轴、y轴、z轴,建立空间直角坐标系.
7.2020·北京第四中学质量检测
如图,正方体的棱长为1,中心为, ,则四面体的体积为 ( )
A. B. C. D.
学审题 (1)宜用几何法求四面体(三棱锥)OEBF的体积吗?以何为底?何为高?底、高容易求吗?
(2)本题若用坐标法,又如何求底面的面积?如何求高?
则,则,
所以,
名校新题聚焦
解析
7.2020·北京第四中学质量检测
如图,正方体的棱长为1,中心为, ,则四面体的体积为 ( )
A. B. C. D.
所以,所以,
设平面的一个法向量为,
由取,得
又所以到平面的距离,
所以四面体OEBF的体积为.
D
对于立体几何问题,若不宜采用几何法处理时,则可考虑运用空间向量的坐标法,如此可以避开抽象、复杂的思维过程.利用空间向量解决立体几何问题的一般步骤:
①观察图形,建立恰当的空间直角坐标系;
②写出相应点的坐标,求出相应直线的方向向量;
③设出相应平面的法向量,利用两直线垂直,其相应方向向量数量积为零列出方程组求出法向量;
④将空间位置关系转化为向量关系;
⑤根据定理结论求出相应的角或距离.
名校新题聚焦
名师综评
名校新题聚焦
解析
如图,取的中点,连接.
∵,,且,
∴是二面角的平面角.
以为原点,所在直线为轴,所在直线为轴,过点作平面的垂线,以此为轴,建立空间直角坐标系,则.
8.2020·深圳中学月考
已知四边形,现将沿折起,使二面角的大小在内,则直线与所成角的余弦值的取值范围是 ( )
A. B. C. D.
学审题 (1)三棱锥中,哪些棱的长度是已知的?各面的三角形有无特殊性?
(2)若用几何法,直线与所成角容易作出吗?其余弦值的范围如何确定?
(3)本题若采用坐标法,该如何建系?如何设出各点的坐标?
(4)如何确定直线与所成角余弦值的范围.
设二面角的平面角为,则,,,
∴.
名校新题聚焦
解析
设直线与的夹角为则,∵.
故.
8.2020·深圳中学月考
已知四边形,现将沿折起,使二面角的大小在内,则直线与所成角的余弦值的取值范围是 ( )
A. B. C. D.
A
名师综评
对于立体几何中的最值和范围问题,我们要知晓:
(1)考什么:常见几何体的体积或表面积的最值和范围,点、面距离的最值和范围,线面角和面面角的最值和范围.
(2)怎么考:主要考查动点问题、翻折问题、组合体问题、几何体与球的外接、内切问题.
(3)怎么办:①画图,将立体几何问题平面化;②将立体几何中的变化值转化为代数式的数值变化.
(4)易错点:注意变量的范围,注意考虑实际意义.
名校新题聚焦
解析
以点为坐标原点, 的方向为x轴、y轴、z轴正方向,建立空间直角坐标系,如图所示.
学审题(1) 二面角的大小为这个条件如何用 其平面角能作出吗
(2)三棱锥的体积如何表示
(3)本题若采用坐标法,该如何建系?如何设相关点的坐标 如何利用条件求的长
∵,
∵底面平面,∴.
又,∴平面,∴即为二面角的平面角.
9.2020.复旦大学附属中学质量检测
在三棱锥中,底面,若,二面角的大小为,三棱锥的体积为,则直线与平面所成角的正弦值为 ( )
A. B. C. D.
又二面角的大小为在中,,
∴,即,∴.
∵三棱锥的体积为,∴,
名校新题聚焦
解析
∴,即.
∵平面,∴平面的一个法向量为.
又,∴.
∵ 直线与平面所成的角,∴.
9.2020.复旦大学附属中学质量检测
在三棱锥中,底面,若,二面角的大小为,三棱锥的体积为,则直线与平面所成角的正弦值为 ( )
A. B. C. D.
C
名师综评
本题把锥体体积、线面角、二面角交汇地考查,其解题的关键是建系后,如何依据条件求出各相关点的坐标.利用空间向量求线面角的注意事项:
(1)先求出直线的方向向量与平面的法向量所夹的锐角(钝角时取其补角)的角度,再取其余角即为所求.
(2)求线面角的余弦值,要注意利用平方关系求出其值,不要误以为直线的方向向量与平面的法向量所夹角的余弦值为所求.
名校新题聚焦
解析
以为坐标原点,建立如图所示的空间直角坐标系,则,,.
10.2020 武汉二中月考
如图,已知三棱柱的侧棱与底面垂直,分别是的中点,点在直线上,且.
(1)证明:无论取何值,总有;
(2)当取何值时,直线与平面所成的角最大 并求该角取最大值时的正切值;
(3)是否存在点,使得平面与平面所成的二面角为 若存在,试确定点的位置;若不存在,请说明理由.
学审题(1)建系后,如何设点的坐标
(2)如何求直线与平面所成角的最大值
(3)如何求平面法向量坐标
(4)如何确定满足条件的点是否存在
∵,∴,∴,.
,无论取何值,总有.
(2)∵是平面的一个法向量,∴,
又当时, 取得最大值,即取得最大值时,∴.
名校新题聚焦
解析
(3)假设存在点满足题意,设是平面的法向量,
由得令,得.
由 知平面的一个法向量为,
10.2020 武汉二中月考
如图,已知三棱柱的侧棱与底面垂直,分别是的中点,点在直线上,且.
(1)证明:无论取何值,总有;
(2)当取何值时,直线与平面所成的角最大 并求该角取最大值时的正切值;
(3)是否存在点,使得平面与平面所成的二面角为 若存在,试确定点的位置;若不存在,请说明理由.
,,化简得.
∵方程无解,
∴不存在点使得平面与平面所成的二面角为
解决立体几何中探索性问题的基本方法:
(1)通常假设题中的数学对象存在(或结论成立),然后在这个前提下进行逻辑推理.
(2)探索性问题的设点方法:①空间中的点可设为;②坐标平面内的点其中一个坐标为0,如平面上的点为,一般平面内的点,如平面内一点,可设为;③坐标轴上的点两个坐标为0,如轴上的点为;④直线(线段)上的点,可设为,表示出点的坐标,或直接利用向量运算.
解这类问题时要利用好向量垂直和平行的坐标表示.
名校新题聚焦
名师综评
《空间向量与立体几何》
人教A版同步教材名师课件
---名校新题聚焦
单元知识导图
1.2020.人民大学附属中学质量检测
某棱锥的三视图如图所示,则该棱雉的外接球的表面积为 ( )
A. B. C. D.
名校新题聚焦
学审题(1)三视图对应的几何体是什么图形
(2)求解几何体外接球问题有哪些方法 该几何体的外接球问题运用几何法易求解吗
(3)若运用代数方法该如何求解
解析
如图,在长、宽、高分别为2,1,1的长方体中,所在棱的中点,由三视图的知识可知,几何体即三棱锥,以为坐标原点建立空间直角坐标系.
A
如图所示,则,设外接球的球心为,半径为,则,于是有解得所以,所以外接球的半径为,表面积为.故选A.
用坐标法求解,要善于借助长方体.将几何体纳入长方体后,各个顶点的坐标容易求出,设出球心坐标,利用球心到球面上各顶点的距离都等于半径,求得球心坐标,进而求得面积.
名校新题聚焦
名师综评
2.2020 长沙长郡中学月考
如图,甲站在水库底面上的点处,乙站在水坝斜面上的点处,已知测得从D,C到库底与水坝的交线的距离分别为的长为 ,CD的长为 则库底与水坝所成的二面角的大小为______.
名校新题聚焦
学审题(1)此题要求什么 易直接求解吗
(2)求二面角的平面角有哪些方法 此题宜采用何种方法
(3)条件中有哪些线段长度已知,它们的位置关系是什么
解析
,
,
.
又,
,
解得,
库底与水坝所成的二面角,故答案为.
本题解题的关键是通过对实际问题的抽象,建立数学模型,进而从向量的角度快速解决.
名校新题聚焦
名师综评
名校新题聚焦
解析
以为坐标原点,射线分别为轴的正方向建立空间直角坐标系(图略),所以球心,故到直线的距离为,而球的半径为,所以在球内的线段长度为.故选A .
3.2020.成都第七中学月考
棱长为1的正方体内有一个内切球,过正方体中两条互为异面直线的的中点作直线,该直线被球面截在球内的线段的长为( )
A. B. C. D.
学审题 (1)正方体内切球半径是多少
(2)要求直线被内切球面截得的线段长,先应求出什么
(3)解决此题有哪些方法可考虑
A
本题的解题关键是求出球心到直线的距离,既可用几何方法也可用坐标法.
名师综评
名校新题聚焦
解析
由题意知内切球的半径为1,设球心为,
则.
.
4.2020·上海中学期末检测
点是底面边长为,高为2的正三棱柱表面上的动点,是该棱柱内切球的一条直径,则的取值范围是_______.
学审题 (1)题中点什么点 有什么特殊性
(2)正三棱柱的内切球半径等于多少
(3)直接求容易吗 需要如何处理
求两向量数量积的常用方法:
(1)直接求,运用求解.
(2)坐标法,运用求解,,.
(3)若直接求较困难,可把转化为其他模与夹角易求的向量再求解.
名师综评
名校新题聚焦
解析
以为坐标原点,建立如图所示的空间直角坐标系,则,
5.2020 河北衡水中学质量检测
如图,在四棱柱中,平面,底面是边长为的正方形,侧棱的长为为侧棱上的动点(包括端点),则( )
A.对任意的,存在点,使得
B.当且仅当,存在点,使得
C.当且仅当,存在点,使得
D.当且仅当,存在点,使得
学审题 (1)图中哪些点是定点,哪些点是动点 (2)如果运用坐标法,该如何表示坐标
(3)由能得到什么结论 (4)如何确定存在所满足的条件
设,则,
所以,令,则,由得,
所以当且仅当时,存在点,使得
B
名师综评
本题也可用三垂线定理,在平面内,探求成立所满足的条件.
名校新题聚焦
解析
以为坐标原点, ,分别以所在的直线为x轴、y轴、z轴,建立空间直角坐标系(图略).
则,设,因为,所以,
所以,
又,
由可得,所以,故线段的长度的最大值为6.
6.2020.华师一附中阶段检测
在长方体中,已知底面为正方形,为的中点,,点是正方形所在平面内的一个动点,且,则线段的长度的最大值为( )
A.8 B.10 C.6 D.12
学审题 (1)解答本题的关键是确定动点Q运动的轨迹,点Q满足什么条件?
(2)确定点Q的轨迹,最好是采用几何法,还是坐标法?
(3)若用坐标法,点Q的坐标如何设?
(4)点Q在什么位置时,线段BQ的长度最大?
C
立体几何中的动点的轨迹确定,解答时通常要根据几何体在相关线段、平面的变化规律,洞悉其变化特点,哪些点、线保持不变,哪些点、线在变化,是按什么规律变化的,进而可将动态固定下来考虑.
名校新题聚焦
名师综评
名校新题聚焦
解析
以为坐标原点, ,分别以所在的直线为x轴、y轴、z轴,建立空间直角坐标系.
7.2020·北京第四中学质量检测
如图,正方体的棱长为1,中心为, ,则四面体的体积为 ( )
A. B. C. D.
学审题 (1)宜用几何法求四面体(三棱锥)OEBF的体积吗?以何为底?何为高?底、高容易求吗?
(2)本题若用坐标法,又如何求底面的面积?如何求高?
则,则,
所以,
名校新题聚焦
解析
7.2020·北京第四中学质量检测
如图,正方体的棱长为1,中心为, ,则四面体的体积为 ( )
A. B. C. D.
所以,所以,
设平面的一个法向量为,
由取,得
又所以到平面的距离,
所以四面体OEBF的体积为.
D
对于立体几何问题,若不宜采用几何法处理时,则可考虑运用空间向量的坐标法,如此可以避开抽象、复杂的思维过程.利用空间向量解决立体几何问题的一般步骤:
①观察图形,建立恰当的空间直角坐标系;
②写出相应点的坐标,求出相应直线的方向向量;
③设出相应平面的法向量,利用两直线垂直,其相应方向向量数量积为零列出方程组求出法向量;
④将空间位置关系转化为向量关系;
⑤根据定理结论求出相应的角或距离.
名校新题聚焦
名师综评
名校新题聚焦
解析
如图,取的中点,连接.
∵,,且,
∴是二面角的平面角.
以为原点,所在直线为轴,所在直线为轴,过点作平面的垂线,以此为轴,建立空间直角坐标系,则.
8.2020·深圳中学月考
已知四边形,现将沿折起,使二面角的大小在内,则直线与所成角的余弦值的取值范围是 ( )
A. B. C. D.
学审题 (1)三棱锥中,哪些棱的长度是已知的?各面的三角形有无特殊性?
(2)若用几何法,直线与所成角容易作出吗?其余弦值的范围如何确定?
(3)本题若采用坐标法,该如何建系?如何设出各点的坐标?
(4)如何确定直线与所成角余弦值的范围.
设二面角的平面角为,则,,,
∴.
名校新题聚焦
解析
设直线与的夹角为则,∵.
故.
8.2020·深圳中学月考
已知四边形,现将沿折起,使二面角的大小在内,则直线与所成角的余弦值的取值范围是 ( )
A. B. C. D.
A
名师综评
对于立体几何中的最值和范围问题,我们要知晓:
(1)考什么:常见几何体的体积或表面积的最值和范围,点、面距离的最值和范围,线面角和面面角的最值和范围.
(2)怎么考:主要考查动点问题、翻折问题、组合体问题、几何体与球的外接、内切问题.
(3)怎么办:①画图,将立体几何问题平面化;②将立体几何中的变化值转化为代数式的数值变化.
(4)易错点:注意变量的范围,注意考虑实际意义.
名校新题聚焦
解析
以点为坐标原点, 的方向为x轴、y轴、z轴正方向,建立空间直角坐标系,如图所示.
学审题(1) 二面角的大小为这个条件如何用 其平面角能作出吗
(2)三棱锥的体积如何表示
(3)本题若采用坐标法,该如何建系?如何设相关点的坐标 如何利用条件求的长
∵,
∵底面平面,∴.
又,∴平面,∴即为二面角的平面角.
9.2020.复旦大学附属中学质量检测
在三棱锥中,底面,若,二面角的大小为,三棱锥的体积为,则直线与平面所成角的正弦值为 ( )
A. B. C. D.
又二面角的大小为在中,,
∴,即,∴.
∵三棱锥的体积为,∴,
名校新题聚焦
解析
∴,即.
∵平面,∴平面的一个法向量为.
又,∴.
∵ 直线与平面所成的角,∴.
9.2020.复旦大学附属中学质量检测
在三棱锥中,底面,若,二面角的大小为,三棱锥的体积为,则直线与平面所成角的正弦值为 ( )
A. B. C. D.
C
名师综评
本题把锥体体积、线面角、二面角交汇地考查,其解题的关键是建系后,如何依据条件求出各相关点的坐标.利用空间向量求线面角的注意事项:
(1)先求出直线的方向向量与平面的法向量所夹的锐角(钝角时取其补角)的角度,再取其余角即为所求.
(2)求线面角的余弦值,要注意利用平方关系求出其值,不要误以为直线的方向向量与平面的法向量所夹角的余弦值为所求.
名校新题聚焦
解析
以为坐标原点,建立如图所示的空间直角坐标系,则,,.
10.2020 武汉二中月考
如图,已知三棱柱的侧棱与底面垂直,分别是的中点,点在直线上,且.
(1)证明:无论取何值,总有;
(2)当取何值时,直线与平面所成的角最大 并求该角取最大值时的正切值;
(3)是否存在点,使得平面与平面所成的二面角为 若存在,试确定点的位置;若不存在,请说明理由.
学审题(1)建系后,如何设点的坐标
(2)如何求直线与平面所成角的最大值
(3)如何求平面法向量坐标
(4)如何确定满足条件的点是否存在
∵,∴,∴,.
,无论取何值,总有.
(2)∵是平面的一个法向量,∴,
又当时, 取得最大值,即取得最大值时,∴.
名校新题聚焦
解析
(3)假设存在点满足题意,设是平面的法向量,
由得令,得.
由 知平面的一个法向量为,
10.2020 武汉二中月考
如图,已知三棱柱的侧棱与底面垂直,分别是的中点,点在直线上,且.
(1)证明:无论取何值,总有;
(2)当取何值时,直线与平面所成的角最大 并求该角取最大值时的正切值;
(3)是否存在点,使得平面与平面所成的二面角为 若存在,试确定点的位置;若不存在,请说明理由.
,,化简得.
∵方程无解,
∴不存在点使得平面与平面所成的二面角为
解决立体几何中探索性问题的基本方法:
(1)通常假设题中的数学对象存在(或结论成立),然后在这个前提下进行逻辑推理.
(2)探索性问题的设点方法:①空间中的点可设为;②坐标平面内的点其中一个坐标为0,如平面上的点为,一般平面内的点,如平面内一点,可设为;③坐标轴上的点两个坐标为0,如轴上的点为;④直线(线段)上的点,可设为,表示出点的坐标,或直接利用向量运算.
解这类问题时要利用好向量垂直和平行的坐标表示.
名校新题聚焦
名师综评
