人教A版(2019)高中数学选择性必修第一册 《空间向量与立体几何---单元专题梳理》名师课件(共44张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 《空间向量与立体几何---单元专题梳理》名师课件(共44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 15:47:00 | ||
图片预览











文档简介
(共44张PPT)
《空间向量与立体几何》
人教A版同步教材名师课件
---章末专题梳理
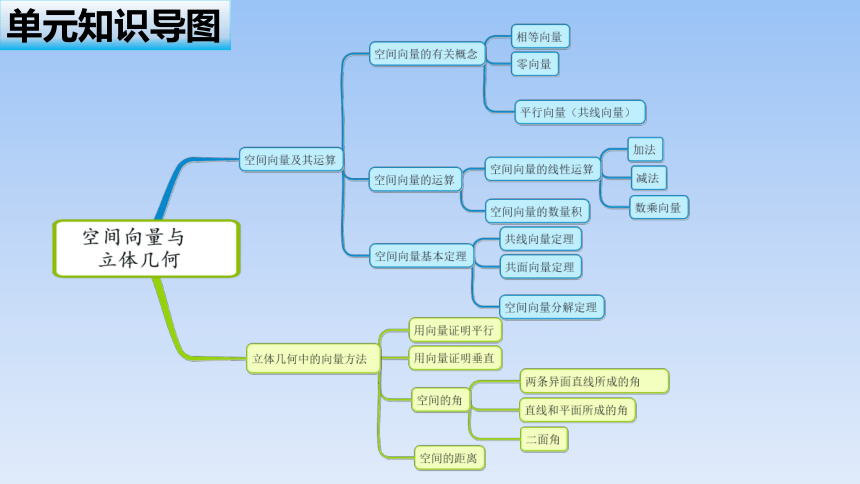
单元知识导图
用已知向量表示未知向量以及进行向量表达式的化简,一定要结合实际图形,以图形为指导是解题的关键,同时注意首尾相接的和向量的化简方法以及从同一个点出发的两个向量的差向量的运算法则,避免出现方向错误.
单元专题梳理
专题1 空间向量的有关概念及线性运算
(1)利用若干个空间向量表示一个空间向量.
典例剖析
解析
单元专题梳理
2020 南京一中单元检测
例1-1如图,已知四边形为正方形,是四边形所在平面外一点,在平面的射影恰好是正方形的中心是的中点,求下列各题中的值:
(1);
(2) .
(1)因为,所以.
(2)因为,所以.
又因为,所以,
所以,
所以.
确定等式中的的值,就是要看怎样用来表示.同理,要确定中的的值,也要把用表示出来.
名师点评
用已知向量表示未知向量以及进行向量表达式的化简,一定要结合实际图形,以图形为指导是解题的关键,同时注意首尾相接的和向量的化简方法以及从同一个点出发的两个向量的差向量的运算法则,避免出现方向错误.
单元专题梳理
专题1 空间向量的有关概念及线性运算
(2)由空间向量的共线关系求参数.
解析
单元专题梳理
2020 福州调考
例1-2已知向量与平行,则__________.
当,即时,,满足.当,即时,因为,所以,解得.综上知,或
本题容易忽略的情形,因为是向量与平行的充分不必要条件.
1或3
典例剖析
名师点评
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(1)利用共顶点的互相垂直的三条棱,构建空间直角坐标系
解析
单元专题梳理
2020·无锡模拟
例2-1已知直四棱柱中,,底面是直角梯形, 为直角,,则异面直线与所成角的余弦值为_______.
如图,以为坐标原点,,所在直线分别为轴、轴、z轴建立空间直角坐标系,则,所以
设与所成的角为,则.
故异面直线与所成角的余弦值为.
由题意可知,在直四棱柱中相互垂直,且交于一点可考虑以点为原点,以三条棱所在的直线为坐标轴建立空间直角坐标系,通过求两异面直线的方向向量的夹角的余弦值,即可得出答案.
典例剖析
名师点评
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(2)利用线面垂直关系,构建空间直角坐标系
解析
单元专题梳理
2020·东北三校联考
例2-2如图,在三条柱中,侧面为棱上异于的一点,.已知.求二面角的平面角的正切值.
如图,以为坐标原点,所在直线分别为轴、z轴,过点且垂直于平面的直线为轴建立空间直角坐标系.
由,知.
设,由,得,
即,
解得或(舍去),则.
典例剖析
解析
单元专题梳理
2020·东北三校联考
例2-2如图,在三条柱中,侧面为棱上异于的一点.已知.求二面角的平面角的正切值.
由已知可得,故二面角的平面角的大小即为向量与的夹角.
因为,所以,所以,故二面角的平面角的正切值为.
已知条件中的垂直关系“侧面”可作为建系的突破口,找二面角的平面角可从定义入手,分别寻找两个半平面内与交线的方向向量垂直的直线的方向向量.
典例剖析
名师点评
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(3)利用面面垂直关系,构建空间直角坐标系
解析
单元专题梳理
2020·太原调考
例2-3在四棱锥中,底面是正方形,侧面是正三角形,平面底面.
(1)证明:平面;(2)求二面角的平面角的余弦值.
取的中点为坐标原点,由题意知,平面,则可建立如图所示的空间直角坐标系.设,则,.
(1)易得.
因为,所以,即.
又,所以平面.
(2)易得,设为的中点,连接,则,所以
.
典例剖析
解析
单元专题梳理
2020·太原调考
例2-3在四棱锥中,底面是正方形,侧面是正三角形,平面底面.
(1)证明:平面;(2)求二面角的平面角的余弦值.
因为,所以,即.
又,所以即为所求二面角的平面角.
所以,故所求二面角的平面角的余弦值为.
已知条件中有面面垂直关系,可考虑以一个面为平面,在另一个平面内找出一条垂直于平面的直线作为轴,从而建立空间直角坐标系.证明线面垂直,只需证明直线与平面内的两条相交直线垂直;找二面角的平面角可从定义入手.
典例剖析
名师点评
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(4)利用正棱锥的中心与高所在的直线,构建空间直角坐标系
解析
单元专题梳理
2020·武汉二中调考
例2-4已知正四棱雉中,为的中点,正四棱锥底面边长为,高为.
(1)求的余弦值;
(2)若,求的余弦值.
(1)如图,以在底面内的正投影为坐标原点建立空间直角坐标系,其中.
由,知.
所以,
所以,
即.
典例剖析
解析
单元专题梳理
2020·武汉二中调考
例2-4已知正四棱雉中,为的中点,正四棱锥底面边长为,高为.
(1)求的余弦值;
(2)若,求的余弦值.
(2)因为,所以,即,所以,所以.
这时,即.
利用正四棱锥的中心与高所在的直线,构建空间直角坐标系.
典例剖析
名师点评
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(5)利用底面正方形的中心,构建空间直角坐标系
解析
单元专题梳理
2020·石家庄高中毕业年级质量检测(二)
例2-5如图,已知平行六面体的底面为正方形, 分别为上、下底面的中心,且在底面上的射影是.
(1)求证:平面平面;
(2)若点分别在棱上,且,问点在何处时,
(1)如图,以为坐标原点,所在直线分别为轴、轴、轴建立空间直角坐标系.
设.
则.
则.
设分别是平面和平面的法向量.
由得令,则,而.
故,即平面的法向量与平面的法向量垂直,故平面平面.
典例剖析
解析
单元专题梳理
2020·石家庄高中毕业年级质量检测(二)
例2-5如图,已知平行六面体的底面为正方形, 分别为上、下底面的中心,且在底面上的射影是.
(1)求证:平面平面;
(2)若点分别在棱上,且,问点在何处时,
(2)由(1)可知, ,
.
设,则,故点的坐标为.
,解得.
故当为的三等分点(靠近时,有
典例剖析
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(6)利用底面正三角形,构建空间直角坐标系
解析
单元专题梳理
江苏高考
例2-6如图,在正三棱柱中,,点分别为的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线与平面所成角的正弦值.
如图,在正三棱柱中,设的中点分别为,连接,则,以为基底,建立空间直角坐标系.
因为,所以.
(1)因为为的中点,所以,从而,
故.
因此,异面直线与所成角的余弦值为.
典例剖析
解析
单元专题梳理
江苏高考
例2-6如图,在正三棱柱中,,点分别为的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线与平面所成角的正弦值.
典例剖析
(2)因为的中点,所以,
因此.
设为平面的法向量,
则即不妨取.
设直线与平面所成角为,则,
所以直线与平面所成角的正弦值为
已知平面,如果一个向量n的基线与平面垂直,则向量n叫作平面的法向量或说向量n与平面正交.法向量的引进,对空间夹角与距离问题以及线面与面面位置关系问题的研究,提供了一个很方便、实用的工具,其思路明确,易于下手,过程较为程序化,易于掌握.
单元专题梳理
专题3 平面的法向量的求法及其应用
(1)求平面的一个法向量
解析
单元专题梳理
2020 衡水中学检测
例3-1已知正方体,求平面的一个法向量.
以为坐标原点,建立如图所示的空间直角坐标系.
设正方体的棱长为1,则有,,所以.
设为平面的法向量,则.
所以所以
令,则.
故平面的一个法向量为.
由向量关系得到的方程组后,一般为两个关系式,三个未知量,通常先给定,再求.对赋值时,常常以“简单”数量为原则.
典例剖析
名师点评
已知平面,如果一个向量n的基线与平面垂直,则向量n叫作平面的法向量或说向量n与平面正交.法向量的引进,对空间夹角与距离问题以及线面与面面位置关系问题的研究,提供了一个很方便、实用的工具,其思路明确,易于下手,过程较为程序化,易于掌握.
单元专题梳理
专题3 平面的法向量的求法及其应用
(2)利用平面的法向量证明位置关系
单元专题梳理
2020·青岛调考节选
例3-2已知在正方体中,分别是,的中点.
求证:平面平面.
如图,建立空间直角坐标系.
解析
令,则有,,.,
设分别是平面,平面的法向量,则.
所以所以令,得.同理可得.所以,知.所以平面平面.
典例剖析
证明平面与平面垂直,可以转化为证明两个平面的法向量垂直.而证明平面与平面平行,可以转化为证明两个平面的法向量平行,并且不需要在图形中作出辅助线,使图形更清楚明了.
名师点评
已知平面,如果一个向量n的基线与平面垂直,则向量n叫作平面的法向量或说向量n与平面正交.法向量的引进,对空间夹角与距离问题以及线面与面面位置关系问题的研究,提供了一个很方便、实用的工具,其思路明确,易于下手,过程较为程序化,易于掌握.
单元专题梳理
专题3 平面的法向量的求法及其应用
(3)利用法向量求空间距离
解析
单元专题梳理
2020·石家庄模拟
例3-3已知正四棱柱,点为中点,则点到平面距离为_______.
以为原点,建立如图所示的空间直角坐标系,则.
所以,
设平面的法向量为.
因为,所以令,得.
又因为,
所以点到平面距离.
典例剖析
名师点评
点到面的距离,就是过该点的某一斜线段的长和斜线与该平面的法向量的夹角的余弦值的绝对值的乘积,即.
单元专题梳理
【拓展】在例题3-3中,求与之间的距离.
解析
异面直线间的距离就是与两直线都相交的线段在公共法向量上的投影.
,
.
设,
所以所以令,得.
因为,所以.
所以与之间的距离为.
求两异面直线间的距离,可先求得两直线的公共法向量,然后在两直线上各取一点,求出过这两点的向量在法向量上的射影长就是两异面直线间的距离,即.
典例剖析
名师点评
已知平面,如果一个向量n的基线与平面垂直,则向量n叫作平面的法向量或说向量n与平面正交.法向量的引进,对空间夹角与距离问题以及线面与面面位置关系问题的研究,提供了一个很方便、实用的工具,其思路明确,易于下手,过程较为程序化,易于掌握.
单元专题梳理
专题3 平面的法向量的求法及其应用
(4)利用法向量求空间角
解析
单元专题梳理
南昌调考节选
例3-4在长方体中,点分别在上,且,求平面与平面所成角的正弦值.
以为原点建立空间直角坐标系,如图所示.
则, ,
设
因为,,所以,所以.
同理可得.所以.
设平面的法向量为,所以所以
令,得.
典例剖析
解析
单元专题梳理
南昌调考节选
例3-4在长方体中,点分别在上,且,求平面与平面所成角的正弦值.
设平面的法向量为,因为,
所以所以令,得.
,
因为平面与平面所成二面角为或,而.
所以平面与平面所成角的正弦值为.
典例剖析
平行、垂直、夹角和距离等问题是立体几何中的主要问题,而以它们为背景的探索性问题是近几年来高考数学命题创新的一个显著特点.由于此类问题所涉及的点具有运动性和不确定性,所以用传统的方法解决起来难度较大,若用向量法处理,尤其是引入坐标表示的空间向量,通过待定系数法求解存在性问题则思路简单,解法固定,操作方便.下面举例谈谈用向量法求解立体几何探索性问题的类型和方法.
单元专题梳理
专题4 立体几何中存在性问题的向量解法
(1)与平行关系有关的存在性问题
解析
单元专题梳理
2020·杭州模拟
例4-1如图,四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,为侧棱上的点.若平面,问侧棱上是否存在一点,使得平面 若存在,求的值;若不存在,试说明理由.
连接,设交于点,连接,由题意知平面为坐标原点, 分别为x轴、y轴、z轴正方向,建立空间直角坐标系,如图所示.
设底面边长为,则,于是,
则.
假设在侧棱上存在一点,使得平面.
由题意知是平面的一个法向量,
设,则.
典例剖析
解析
单元专题梳理
2020·杭州模拟
例4-1如图,四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,为侧棱上的点.若平面,问侧棱上是否存在一点使得平面 若存在,求的值;若不存在,试说明理由.
由,得,解得.
即当时, ,又平面,
所以侧棱上存在一点,使得平面.
有关是否存在一点,使得直线与平面之间满足平行的探索性问題,在解答时,先假设存在这样的点,再建立空间直角坐标系,设出该点的坐标,将直线与平面的平行关系转化为直线的方向向量与平面的法向量的关系,利用向量坐标运算建立关于所求点坐标的方程(组),若方程(组)有解,则点存在;否则,点不存在.
典例剖析
名师点评
平行、垂直、夹角和距离等问题是立体几何中的主要问题,而以它们为背景的探索性问题是近几年来高考数学命题创新的一个显著特点.由于此类问题所涉及的点具有运动性和不确定性,所以用传统的方法解决起来难度较大,若用向量法处理,尤其是引入坐标表示的空间向量,通过待定系数法求解存在性问题则思路简单,解法固定,操作方便.下面举例谈谈用向量法求解立体几何探索性问题的类型和方法.
单元专题梳理
专题4 立体几何中存在性问题的向量解法
(2)与垂直关系有关的存在性问题
解析
单元专题梳理
2020·黄冈中学单元测试
例4-2在长方体中,为对角线的中点,若为上的一动点,当在何处时,平面平面?
建立如图所示的空间直角坐标系,则,,
所以.
设,则.
设为平面的法向量,
则有即则
典例剖析
解析
单元专题梳理
例 2020·黄冈中学单元测试
4-2在长方体中,为对角线的中点,若为上的一动点,当在何处时,平面平面?
取,可得平面的一个法向量为.
同理,可求得平面的一个法向量为.
若平面平面,则有,即,解得.
故当为AB的中点时,平面平面.
有关是否存在一点,使得直线与平面之间满足垂直的探索性问题,解答时,先假设存在这样的点,再建立空间直角坐标系,设出该点的坐标,将直线与平面的垂直关系转化为直线的方向向量与平面的法向量的关系,利用向量坐标运算建立关于所求点坐标的方程(组).若方程(组)有解,则点存在;否则,点不存在.
典例剖析
名师点评
平行、垂直、夹角和距离等问题是立体几何中的主要问题,而以它们为背景的探索性问题是近几年来高考数学命题创新的一个显著特点.由于此类问题所涉及的点具有运动性和不确定性,所以用传统的方法解决起来难度较大,若用向量法处理,尤其是引入坐标表示的空间向量,通过待定系数法求解存在性问题则思路简单,解法固定,操作方便.下面举例谈谈用向量法求解立体几何探索性问题的类型和方法.
单元专题梳理
专题4 立体几何中存在性问题的向量解法
(3)与夹角有关的存在性问题
解析
单元专题梳理
2020·长沙一中单元检测
例4-3在正三棱柱中,所有棱的长度都是是边的中点,试问:侧棱上是否存在一点,使得异面直线和所成的角等于
以A为坐标原点,建立如图所示的空间直角坐标系.因为所有棱长都等于2,
所以,假设侧棱上存在点满足题意,可设,则.于是.如果异面直线和所成的角等于 ,那么向量和的夹角是或,而,所以,解得,与矛盾.所以侧棱上不存在点,使得异面直线和所成的角等于 .
典例剖析
名师点评
求两异面直线所成的角、直线与平面所成的角和二面角是立体几何中与角有关的主要问题,利用向量法解决此类问题可以避开抽象、复杂地寻找角的过程,只要能够准确理解和熟 应用公式(其中为两直线的方向向量或为两平面的法向量),就可以使此类问题巧妙获解.
平行、垂直、夹角和距离等问题是立体几何中的主要问题,而以它们为背景的探索性问题是近几年来高考数学命题创新的一个显著特点.由于此类问题所涉及的点具有运动性和不确定性,所以用传统的方法解决起来难度较大,若用向量法处理,尤其是引入坐标表示的空间向量,通过待定系数法求解存在性问题则思路简单,解法固定,操作方便.下面举例谈谈用向量法求解立体几何探索性问题的类型和方法.
单元专题梳理
专题4 立体几何中存在性问题的向量解法
(4)与距离有关的存在性问题
解析
单元专题梳理
2020·合肥二中单元检测
例4-4直三棱柱中,底面是等腰三角形, ,侧棱是的中点.试问:线段(不包括端点)上是否存在一点,使得点到平面的距离为
如图,以所在直线分别为x轴、y轴、z轴,建立空间直角标系,则,所以.
假设线段(不包括端点)上存在一点,使到平面的距离为.
设点到的距离为,则.
设向量为平面的法向量,则有,即
典例剖析
解析
单元专题梳理
2020·合肥二中单元检测
例4-4直三棱柱中,底面是等腰三角形, ,侧棱是的中点.试问:线段(不包括端点)上是否存在一点,使得点到平面的距离为
取,可得平面的一个法向量为.
由题意可知,解得或(舍去),所以.
所以当为线段的中点时,点到平面的距离为
立体几何中的点面距离、线面距离和面面距离等都可由公式来解决,其中向量n为平面的法向量,向量为该点或线(面)上任意一点与平面上任意一点所构成的向量.
典例剖析
名师点评
《空间向量与立体几何》
人教A版同步教材名师课件
---章末专题梳理
单元知识导图
用已知向量表示未知向量以及进行向量表达式的化简,一定要结合实际图形,以图形为指导是解题的关键,同时注意首尾相接的和向量的化简方法以及从同一个点出发的两个向量的差向量的运算法则,避免出现方向错误.
单元专题梳理
专题1 空间向量的有关概念及线性运算
(1)利用若干个空间向量表示一个空间向量.
典例剖析
解析
单元专题梳理
2020 南京一中单元检测
例1-1如图,已知四边形为正方形,是四边形所在平面外一点,在平面的射影恰好是正方形的中心是的中点,求下列各题中的值:
(1);
(2) .
(1)因为,所以.
(2)因为,所以.
又因为,所以,
所以,
所以.
确定等式中的的值,就是要看怎样用来表示.同理,要确定中的的值,也要把用表示出来.
名师点评
用已知向量表示未知向量以及进行向量表达式的化简,一定要结合实际图形,以图形为指导是解题的关键,同时注意首尾相接的和向量的化简方法以及从同一个点出发的两个向量的差向量的运算法则,避免出现方向错误.
单元专题梳理
专题1 空间向量的有关概念及线性运算
(2)由空间向量的共线关系求参数.
解析
单元专题梳理
2020 福州调考
例1-2已知向量与平行,则__________.
当,即时,,满足.当,即时,因为,所以,解得.综上知,或
本题容易忽略的情形,因为是向量与平行的充分不必要条件.
1或3
典例剖析
名师点评
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(1)利用共顶点的互相垂直的三条棱,构建空间直角坐标系
解析
单元专题梳理
2020·无锡模拟
例2-1已知直四棱柱中,,底面是直角梯形, 为直角,,则异面直线与所成角的余弦值为_______.
如图,以为坐标原点,,所在直线分别为轴、轴、z轴建立空间直角坐标系,则,所以
设与所成的角为,则.
故异面直线与所成角的余弦值为.
由题意可知,在直四棱柱中相互垂直,且交于一点可考虑以点为原点,以三条棱所在的直线为坐标轴建立空间直角坐标系,通过求两异面直线的方向向量的夹角的余弦值,即可得出答案.
典例剖析
名师点评
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(2)利用线面垂直关系,构建空间直角坐标系
解析
单元专题梳理
2020·东北三校联考
例2-2如图,在三条柱中,侧面为棱上异于的一点,.已知.求二面角的平面角的正切值.
如图,以为坐标原点,所在直线分别为轴、z轴,过点且垂直于平面的直线为轴建立空间直角坐标系.
由,知.
设,由,得,
即,
解得或(舍去),则.
典例剖析
解析
单元专题梳理
2020·东北三校联考
例2-2如图,在三条柱中,侧面为棱上异于的一点.已知.求二面角的平面角的正切值.
由已知可得,故二面角的平面角的大小即为向量与的夹角.
因为,所以,所以,故二面角的平面角的正切值为.
已知条件中的垂直关系“侧面”可作为建系的突破口,找二面角的平面角可从定义入手,分别寻找两个半平面内与交线的方向向量垂直的直线的方向向量.
典例剖析
名师点评
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(3)利用面面垂直关系,构建空间直角坐标系
解析
单元专题梳理
2020·太原调考
例2-3在四棱锥中,底面是正方形,侧面是正三角形,平面底面.
(1)证明:平面;(2)求二面角的平面角的余弦值.
取的中点为坐标原点,由题意知,平面,则可建立如图所示的空间直角坐标系.设,则,.
(1)易得.
因为,所以,即.
又,所以平面.
(2)易得,设为的中点,连接,则,所以
.
典例剖析
解析
单元专题梳理
2020·太原调考
例2-3在四棱锥中,底面是正方形,侧面是正三角形,平面底面.
(1)证明:平面;(2)求二面角的平面角的余弦值.
因为,所以,即.
又,所以即为所求二面角的平面角.
所以,故所求二面角的平面角的余弦值为.
已知条件中有面面垂直关系,可考虑以一个面为平面,在另一个平面内找出一条垂直于平面的直线作为轴,从而建立空间直角坐标系.证明线面垂直,只需证明直线与平面内的两条相交直线垂直;找二面角的平面角可从定义入手.
典例剖析
名师点评
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(4)利用正棱锥的中心与高所在的直线,构建空间直角坐标系
解析
单元专题梳理
2020·武汉二中调考
例2-4已知正四棱雉中,为的中点,正四棱锥底面边长为,高为.
(1)求的余弦值;
(2)若,求的余弦值.
(1)如图,以在底面内的正投影为坐标原点建立空间直角坐标系,其中.
由,知.
所以,
所以,
即.
典例剖析
解析
单元专题梳理
2020·武汉二中调考
例2-4已知正四棱雉中,为的中点,正四棱锥底面边长为,高为.
(1)求的余弦值;
(2)若,求的余弦值.
(2)因为,所以,即,所以,所以.
这时,即.
利用正四棱锥的中心与高所在的直线,构建空间直角坐标系.
典例剖析
名师点评
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(5)利用底面正方形的中心,构建空间直角坐标系
解析
单元专题梳理
2020·石家庄高中毕业年级质量检测(二)
例2-5如图,已知平行六面体的底面为正方形, 分别为上、下底面的中心,且在底面上的射影是.
(1)求证:平面平面;
(2)若点分别在棱上,且,问点在何处时,
(1)如图,以为坐标原点,所在直线分别为轴、轴、轴建立空间直角坐标系.
设.
则.
则.
设分别是平面和平面的法向量.
由得令,则,而.
故,即平面的法向量与平面的法向量垂直,故平面平面.
典例剖析
解析
单元专题梳理
2020·石家庄高中毕业年级质量检测(二)
例2-5如图,已知平行六面体的底面为正方形, 分别为上、下底面的中心,且在底面上的射影是.
(1)求证:平面平面;
(2)若点分别在棱上,且,问点在何处时,
(2)由(1)可知, ,
.
设,则,故点的坐标为.
,解得.
故当为的三等分点(靠近时,有
典例剖析
坐标法是利用空间向量的坐标运算解决立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.
抓住空间几何图形的结构特征,充分利用图形中的垂直关系(或在图形中构造垂直关系)是我们构建空间直角坐标系时的重要依据.下面举例说明几种常见的空间直角坐标系的构建策略.
单元专题梳理
专题2 空间直角坐标系的构建策略
(6)利用底面正三角形,构建空间直角坐标系
解析
单元专题梳理
江苏高考
例2-6如图,在正三棱柱中,,点分别为的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线与平面所成角的正弦值.
如图,在正三棱柱中,设的中点分别为,连接,则,以为基底,建立空间直角坐标系.
因为,所以.
(1)因为为的中点,所以,从而,
故.
因此,异面直线与所成角的余弦值为.
典例剖析
解析
单元专题梳理
江苏高考
例2-6如图,在正三棱柱中,,点分别为的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线与平面所成角的正弦值.
典例剖析
(2)因为的中点,所以,
因此.
设为平面的法向量,
则即不妨取.
设直线与平面所成角为,则,
所以直线与平面所成角的正弦值为
已知平面,如果一个向量n的基线与平面垂直,则向量n叫作平面的法向量或说向量n与平面正交.法向量的引进,对空间夹角与距离问题以及线面与面面位置关系问题的研究,提供了一个很方便、实用的工具,其思路明确,易于下手,过程较为程序化,易于掌握.
单元专题梳理
专题3 平面的法向量的求法及其应用
(1)求平面的一个法向量
解析
单元专题梳理
2020 衡水中学检测
例3-1已知正方体,求平面的一个法向量.
以为坐标原点,建立如图所示的空间直角坐标系.
设正方体的棱长为1,则有,,所以.
设为平面的法向量,则.
所以所以
令,则.
故平面的一个法向量为.
由向量关系得到的方程组后,一般为两个关系式,三个未知量,通常先给定,再求.对赋值时,常常以“简单”数量为原则.
典例剖析
名师点评
已知平面,如果一个向量n的基线与平面垂直,则向量n叫作平面的法向量或说向量n与平面正交.法向量的引进,对空间夹角与距离问题以及线面与面面位置关系问题的研究,提供了一个很方便、实用的工具,其思路明确,易于下手,过程较为程序化,易于掌握.
单元专题梳理
专题3 平面的法向量的求法及其应用
(2)利用平面的法向量证明位置关系
单元专题梳理
2020·青岛调考节选
例3-2已知在正方体中,分别是,的中点.
求证:平面平面.
如图,建立空间直角坐标系.
解析
令,则有,,.,
设分别是平面,平面的法向量,则.
所以所以令,得.同理可得.所以,知.所以平面平面.
典例剖析
证明平面与平面垂直,可以转化为证明两个平面的法向量垂直.而证明平面与平面平行,可以转化为证明两个平面的法向量平行,并且不需要在图形中作出辅助线,使图形更清楚明了.
名师点评
已知平面,如果一个向量n的基线与平面垂直,则向量n叫作平面的法向量或说向量n与平面正交.法向量的引进,对空间夹角与距离问题以及线面与面面位置关系问题的研究,提供了一个很方便、实用的工具,其思路明确,易于下手,过程较为程序化,易于掌握.
单元专题梳理
专题3 平面的法向量的求法及其应用
(3)利用法向量求空间距离
解析
单元专题梳理
2020·石家庄模拟
例3-3已知正四棱柱,点为中点,则点到平面距离为_______.
以为原点,建立如图所示的空间直角坐标系,则.
所以,
设平面的法向量为.
因为,所以令,得.
又因为,
所以点到平面距离.
典例剖析
名师点评
点到面的距离,就是过该点的某一斜线段的长和斜线与该平面的法向量的夹角的余弦值的绝对值的乘积,即.
单元专题梳理
【拓展】在例题3-3中,求与之间的距离.
解析
异面直线间的距离就是与两直线都相交的线段在公共法向量上的投影.
,
.
设,
所以所以令,得.
因为,所以.
所以与之间的距离为.
求两异面直线间的距离,可先求得两直线的公共法向量,然后在两直线上各取一点,求出过这两点的向量在法向量上的射影长就是两异面直线间的距离,即.
典例剖析
名师点评
已知平面,如果一个向量n的基线与平面垂直,则向量n叫作平面的法向量或说向量n与平面正交.法向量的引进,对空间夹角与距离问题以及线面与面面位置关系问题的研究,提供了一个很方便、实用的工具,其思路明确,易于下手,过程较为程序化,易于掌握.
单元专题梳理
专题3 平面的法向量的求法及其应用
(4)利用法向量求空间角
解析
单元专题梳理
南昌调考节选
例3-4在长方体中,点分别在上,且,求平面与平面所成角的正弦值.
以为原点建立空间直角坐标系,如图所示.
则, ,
设
因为,,所以,所以.
同理可得.所以.
设平面的法向量为,所以所以
令,得.
典例剖析
解析
单元专题梳理
南昌调考节选
例3-4在长方体中,点分别在上,且,求平面与平面所成角的正弦值.
设平面的法向量为,因为,
所以所以令,得.
,
因为平面与平面所成二面角为或,而.
所以平面与平面所成角的正弦值为.
典例剖析
平行、垂直、夹角和距离等问题是立体几何中的主要问题,而以它们为背景的探索性问题是近几年来高考数学命题创新的一个显著特点.由于此类问题所涉及的点具有运动性和不确定性,所以用传统的方法解决起来难度较大,若用向量法处理,尤其是引入坐标表示的空间向量,通过待定系数法求解存在性问题则思路简单,解法固定,操作方便.下面举例谈谈用向量法求解立体几何探索性问题的类型和方法.
单元专题梳理
专题4 立体几何中存在性问题的向量解法
(1)与平行关系有关的存在性问题
解析
单元专题梳理
2020·杭州模拟
例4-1如图,四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,为侧棱上的点.若平面,问侧棱上是否存在一点,使得平面 若存在,求的值;若不存在,试说明理由.
连接,设交于点,连接,由题意知平面为坐标原点, 分别为x轴、y轴、z轴正方向,建立空间直角坐标系,如图所示.
设底面边长为,则,于是,
则.
假设在侧棱上存在一点,使得平面.
由题意知是平面的一个法向量,
设,则.
典例剖析
解析
单元专题梳理
2020·杭州模拟
例4-1如图,四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,为侧棱上的点.若平面,问侧棱上是否存在一点使得平面 若存在,求的值;若不存在,试说明理由.
由,得,解得.
即当时, ,又平面,
所以侧棱上存在一点,使得平面.
有关是否存在一点,使得直线与平面之间满足平行的探索性问題,在解答时,先假设存在这样的点,再建立空间直角坐标系,设出该点的坐标,将直线与平面的平行关系转化为直线的方向向量与平面的法向量的关系,利用向量坐标运算建立关于所求点坐标的方程(组),若方程(组)有解,则点存在;否则,点不存在.
典例剖析
名师点评
平行、垂直、夹角和距离等问题是立体几何中的主要问题,而以它们为背景的探索性问题是近几年来高考数学命题创新的一个显著特点.由于此类问题所涉及的点具有运动性和不确定性,所以用传统的方法解决起来难度较大,若用向量法处理,尤其是引入坐标表示的空间向量,通过待定系数法求解存在性问题则思路简单,解法固定,操作方便.下面举例谈谈用向量法求解立体几何探索性问题的类型和方法.
单元专题梳理
专题4 立体几何中存在性问题的向量解法
(2)与垂直关系有关的存在性问题
解析
单元专题梳理
2020·黄冈中学单元测试
例4-2在长方体中,为对角线的中点,若为上的一动点,当在何处时,平面平面?
建立如图所示的空间直角坐标系,则,,
所以.
设,则.
设为平面的法向量,
则有即则
典例剖析
解析
单元专题梳理
例 2020·黄冈中学单元测试
4-2在长方体中,为对角线的中点,若为上的一动点,当在何处时,平面平面?
取,可得平面的一个法向量为.
同理,可求得平面的一个法向量为.
若平面平面,则有,即,解得.
故当为AB的中点时,平面平面.
有关是否存在一点,使得直线与平面之间满足垂直的探索性问题,解答时,先假设存在这样的点,再建立空间直角坐标系,设出该点的坐标,将直线与平面的垂直关系转化为直线的方向向量与平面的法向量的关系,利用向量坐标运算建立关于所求点坐标的方程(组).若方程(组)有解,则点存在;否则,点不存在.
典例剖析
名师点评
平行、垂直、夹角和距离等问题是立体几何中的主要问题,而以它们为背景的探索性问题是近几年来高考数学命题创新的一个显著特点.由于此类问题所涉及的点具有运动性和不确定性,所以用传统的方法解决起来难度较大,若用向量法处理,尤其是引入坐标表示的空间向量,通过待定系数法求解存在性问题则思路简单,解法固定,操作方便.下面举例谈谈用向量法求解立体几何探索性问题的类型和方法.
单元专题梳理
专题4 立体几何中存在性问题的向量解法
(3)与夹角有关的存在性问题
解析
单元专题梳理
2020·长沙一中单元检测
例4-3在正三棱柱中,所有棱的长度都是是边的中点,试问:侧棱上是否存在一点,使得异面直线和所成的角等于
以A为坐标原点,建立如图所示的空间直角坐标系.因为所有棱长都等于2,
所以,假设侧棱上存在点满足题意,可设,则.于是.如果异面直线和所成的角等于 ,那么向量和的夹角是或,而,所以,解得,与矛盾.所以侧棱上不存在点,使得异面直线和所成的角等于 .
典例剖析
名师点评
求两异面直线所成的角、直线与平面所成的角和二面角是立体几何中与角有关的主要问题,利用向量法解决此类问题可以避开抽象、复杂地寻找角的过程,只要能够准确理解和熟 应用公式(其中为两直线的方向向量或为两平面的法向量),就可以使此类问题巧妙获解.
平行、垂直、夹角和距离等问题是立体几何中的主要问题,而以它们为背景的探索性问题是近几年来高考数学命题创新的一个显著特点.由于此类问题所涉及的点具有运动性和不确定性,所以用传统的方法解决起来难度较大,若用向量法处理,尤其是引入坐标表示的空间向量,通过待定系数法求解存在性问题则思路简单,解法固定,操作方便.下面举例谈谈用向量法求解立体几何探索性问题的类型和方法.
单元专题梳理
专题4 立体几何中存在性问题的向量解法
(4)与距离有关的存在性问题
解析
单元专题梳理
2020·合肥二中单元检测
例4-4直三棱柱中,底面是等腰三角形, ,侧棱是的中点.试问:线段(不包括端点)上是否存在一点,使得点到平面的距离为
如图,以所在直线分别为x轴、y轴、z轴,建立空间直角标系,则,所以.
假设线段(不包括端点)上存在一点,使到平面的距离为.
设点到的距离为,则.
设向量为平面的法向量,则有,即
典例剖析
解析
单元专题梳理
2020·合肥二中单元检测
例4-4直三棱柱中,底面是等腰三角形, ,侧棱是的中点.试问:线段(不包括端点)上是否存在一点,使得点到平面的距离为
取,可得平面的一个法向量为.
由题意可知,解得或(舍去),所以.
所以当为线段的中点时,点到平面的距离为
立体几何中的点面距离、线面距离和面面距离等都可由公式来解决,其中向量n为平面的法向量,向量为该点或线(面)上任意一点与平面上任意一点所构成的向量.
典例剖析
名师点评
