人教A版(2019)高中数学选择性必修第一册 空间向量与立体几何(单元测试卷)_练习(含答案)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 空间向量与立体几何(单元测试卷)_练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 16:13:40 | ||
图片预览




文档简介
《空间向量与立体几何》单元测试卷
一、单选题
1.(2020·山东省微山县第二中学高二月考)空间直角坐标中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB与CD的位置关系是( )
A.平行 B.垂直
C.相交但不垂直 D.无法确定
2.(2019·四川省绵阳南山中学高二月考)如图,在平行六面体中,为与的交点若,,,则下列向量中与相等的向量是( )
A. B.
C. D.
3.(2019·江苏省高二期中)已知向量,.若向量与向量平行,则实数的值是( )
A.2 B. C.10 D.
4.(2020·湖南省高二期末)如图,已知正方体ABCD﹣A'B'C'D'中,E是CC'的中点,,,,xyz,则( )
A.x=1,y=2,z=3 B.x,y=1,z=1
C.x=1,y=2,z=2 D.x,y=1,z
5.(2020·四川省双流中学高二月考)正方体不在同一侧面上的两顶点,,则正方体外接球体积是( )
A. B. C. D.
6.(2019·江苏省苏州实验中学高二月考)已知,若点D是AC中点,则( )
A.2 B. C.-3 D.6
7.(2019·江苏省苏州实验中学高二月考)平行六面体中,,则实数x,y,z的值分别为( )
A. B. C. D.
8.(2020·银川唐徕回民中学高二月考)三棱柱中,底面边长和侧棱长都相等,,则异面直线与所成角的余弦值为( )
A. B. C. D.
9.(2019·浙江省柯桥中学高二期中)如图,在三棱柱中,底面,,,则与平面所成角的大小为
A. B. C. D.
10.(2020·山西省高二期末)在一直角坐标系中,已知,现沿轴将坐标平面折成的二面角,则折叠后两点间的距离为( )
A. B. C. D.2
二、多选题
11.(2019·江苏省南京师大附中高二期中)已知点P是平行四边形ABCD所在的平面外一点,如果,,,下列结论正确的有( )
A. B.
C.是平面ABCD的一个法向量 D.
12.(2020·福建省高二期末)在正方体中,,分别是和的中点,则下列结论正确的是( )
A.平面 B.平面
C. D.点与点到平面的距离相等
13.(2020·江苏省启东中学高二开学考试)在正三棱柱中,所有棱长为1,又与交于点,则( )
A.= B.
C.三棱锥的体积为 D.与平面BB′C′C所成的角为
三、填空题
14.(2020·山东省微山县第二中学高二月考)已知向量2,,x,,且,则x的值为______.
15.(2020·河南省高二期末)若向量,,且与的夹角为钝角,则实数的取值范围为________.
16.(2019·山东省济南一中高二期中)如图所示,在正方体中,M为棱的中点,则异面线与AM所成角的余弦值为________.
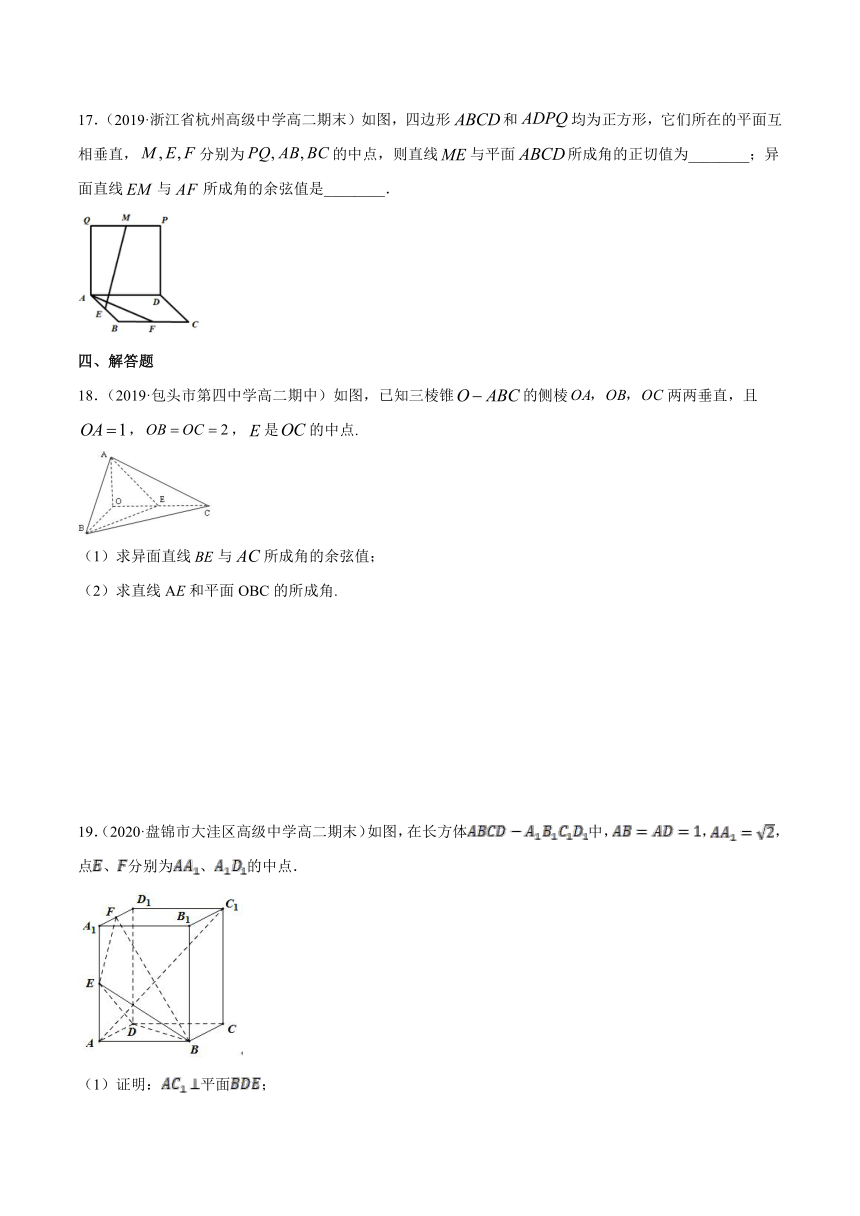
17.(2019·浙江省杭州高级中学高二期末)如图,四边形和均为正方形,它们所在的平面互相垂直,分别为的中点,则直线与平面所成角的正切值为________;异面直线与所成角的余弦值是________.
四、解答题
18.(2019·包头市第四中学高二期中)如图,已知三棱锥的侧棱两两垂直,且,,是的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线AE和平面OBC的所成角.
19.(2020·盘锦市大洼区高级中学高二期末)如图,在长方体中,,,点、分别为、的中点.
(1)证明:平面;
(2)求二面角的余弦值.
20.(2020·盘锦市大洼区高级中学高二期末)如下图所示,在四棱锥中,底面四边形,四边形是直角梯形,且,,点是棱的中点,是上的点,且.
(1)求异面直线与所成的角的余弦值;
(2)求与平面所成的角的正弦值.
21.(2019·山西省长治市第二中学校高二月考)如图,在正方体中,分别是的中点。
(1)求异面直线与所成角的余弦值;
(2)棱上是否存在点,使得平面?请证明你的结论。
22.(2019·绍兴市教育教学研究院高二期末)如图,平面,,交于点.
(1)证明:;
(2)求直线与平面所成角的正弦值.
23.(2019·安徽省高二期中)如图,在四棱锥中,已知平面,且四边形为直角梯形,,,.
(1)求平面与平面所成锐二面角的余弦值;
(2)点是线段上的动点,当直线与所成的角最小时,求线段的长.
《空间向量与立体几何》单元测试卷答案
一、单选题
1.(2020·山东省微山县第二中学高二月考)空间直角坐标中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB与CD的位置关系是( )
A.平行 B.垂直
C.相交但不垂直 D.无法确定
【答案】A
【解析】
∵空间直角坐标系中,A(1,2,3),B(﹣1,0,5),C(3,0,4),D(4,1,3),
∴=(﹣2,﹣2,2),=(1,1,﹣1),∴=﹣2,∴直线AB与CD平行.故选:A.
2.(2019·四川省绵阳南山中学高二月考)如图,在平行六面体中,为与的交点若,,,则下列向量中与相等的向量是( )
A. B.
C. D.
【答案】A
【解析】如图所示,,,
.故选:A
3.(2019·江苏省高二期中)已知向量,.若向量与向量平行,则实数的值是( )
A.2 B. C.10 D.
【答案】A
【解析】
由已知,,因为与共线,所以存在实数,使得,故
,即,解得.故选:A.
4.(2020·湖南省高二期末)如图,已知正方体ABCD﹣A'B'C'D'中,E是CC'的中点,,,,xyz,则( )
A.x=1,y=2,z=3 B.x,y=1,z=1
C.x=1,y=2,z=2 D.x,y=1,z
【答案】A
【解析】
. 故选:A
5.(2020·四川省双流中学高二月考)正方体不在同一侧面上的两顶点,,则正方体外接球体积是( )
A. B. C. D.
【答案】A
【解析】
容易知:是正方体的体对角线上的两点坐标,
故正方体外接球半径为,故.故选:A.
6.(2019·江苏省苏州实验中学高二月考)已知,若点D是AC中点,则( )
A.2 B. C.-3 D.6
【答案】D
【解析】
,,,.故选:D.
7.(2019·江苏省苏州实验中学高二月考)平行六面体中,,则实数x,y,z的值分别为( )
A. B. C. D.
【答案】C
【解析】
,.故选:C.
8.(2020·银川唐徕回民中学高二月考)三棱柱中,底面边长和侧棱长都相等,,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】B
【解析】
设棱长为1,,,,由题意得:,,.
,,
又,
,
,即异面直线与所成角的余弦值为:
本题正确选项:
9.(2019·浙江省柯桥中学高二期中)如图,在三棱柱中,底面,,,则与平面所成角的大小为
A. B. C. D.
【答案】A
【解析】
取AB的中点D,连接CD,以AD为x轴,以CD为y轴,以为z轴,建立空间直角坐标系,
可得,,故,而,设平面的法向量为,根据,解得,.故与平面所成角的大小为,故选A.
10.(2020·山西省高二期末)在一直角坐标系中,已知,现沿轴将坐标平面折成的二面角,则折叠后两点间的距离为( )
A. B. C. D.2
【答案】D
【解析】
如图为折叠后的图形,其中作
则,
沿轴将坐标平面折成的二面角两异面直线所成的角为.
可得:,故由,得
.故选:D.
二、多选题
11.(2019·江苏省南京师大附中高二期中)已知点P是平行四边形ABCD所在的平面外一点,如果,,,下列结论正确的有( )
A. B.
C.是平面ABCD的一个法向量 D.
【答案】ABC
【解析】
因为,,所以A,B正确,因为所以是平面ABCD的一个法向量,所以C正确,,不满足,则D不正确.故选:ABC.
12.(2020·福建省高二期末)在正方体中,,分别是和的中点,则下列结论正确的是( )
A.平面 B.平面
C. D.点与点到平面的距离相等
【答案】AC
【解析】
对A,因为,分别是和的中点故,故平面成立.对B,建立如图空间直角坐标系,
设正方体边长为2则,.故.故不互相垂直.又属于平面.故平面不成立.对C,同B空间直角坐标系有,.故成立.对D, 点与点到平面的距离相等则点与点中点在平面上.连接易得平面即平面.又点与点中点在上,故点不在平面上.故D不成立. 故选:AC
13.(2020·江苏省启东中学高二开学考试)在正三棱柱中,所有棱长为1,又与交于点,则( )
A.= B.
C.三棱锥的体积为 D.与平面BB′C′C所成的角为
【答案】AC
【解析】
由题意,画出正三棱柱如图所示,
向量,故选项A正确;在中,,,,,所以和不垂直,故选项B错误;在三棱锥中,,点到平面的距离即△中边上的高,所以,所以,故选项C正确;设中点为,所以,又三棱柱是正三棱柱,所以平面,所以即与平面BB′C′C所成的角,,所以,故选项D错误.故选:AC
三、填空题
14.(2020·山东省微山县第二中学高二月考)已知向量2,,x,,且,则x的值为______.
【答案】8
【解析】,解得.
15.(2020·河南省高二期末)若向量,,且与的夹角为钝角,则实数的取值范围为________.
【答案】且
【解析】由与的夹角为钝角可得且与不共线,则即且. 故答案为:且.
16.(2019·山东省济南一中高二期中)如图所示,在正方体中,M为棱的中点,则异面线与AM所成角的余弦值为________.
【答案】
【解析】
分别以的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,
不妨设正方体的棱长为1,则,可得,则,即异面直线与AM所成角的余弦值为. 故答案为:
17.(2019·浙江省杭州高级中学高二期末)如图,四边形和均为正方形,它们所在的平面互相垂直,分别为的中点,则直线与平面所成角的正切值为________;异面直线与所成角的余弦值是________.
【答案】,
【解析】
由两两垂直,分别以所在的直线为轴建立如图所示的空间直角坐标系,设,则,所以,其中平面的一个法向量为,所以与平面所成角的正弦值为,所以;又向量与所成角的余弦值为,又,所以异面直线与所成角的余弦值是.
四、解答题
18.(2019·包头市第四中学高二期中)如图,已知三棱锥的侧棱两两垂直,且,,是的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线AE和平面OBC的所成角.
【答案】(1);(2)
【解析】
建立如图所示的空间直角坐标系,则,,
(1),,故,所以异面直线与所成角的余弦值为.
(2)平面的法向量为,,故,因,故,故与平面所成的角为.
19.(2020·盘锦市大洼区高级中学高二期末)如图,在长方体中,,,点、分别为、的中点.
(1)证明:平面;
(2)求二面角的余弦值.
【答案】(1)见证明;(2)
【解析】
(1)如图,以点A为坐标原点,分别以AB,AD,A为x,y,z轴建立空间直角坐标系
则A(0,0,0),B(1,0,0),D(0,1,0),E(0,0,),(1,1,),,,
,,
与BE是平面BDE内两条相交直线,平面BDE
(2)由(1)进一步可得F(0,),,设平面BDE的法向量为,可取,
设平面FBE的法向量为,,由,可得,取x=1,可得(1,-2,)
. 由于二面角F-BE-D为锐二面角,故所求的二面角的余弦值为
20.(2020·盘锦市大洼区高级中学高二期末)如下图所示,在四棱锥中,底面四边形,四边形是直角梯形,且,,点是棱的中点,是上的点,且.
(1)求异面直线与所成的角的余弦值;
(2)求与平面所成的角的正弦值.
【答案】(1); (2).
【解析】 (1)建系以为原点,如图,,
所以,
(2),,设是平面的法向量,
则,即,取,,所以与平面所成的角的正弦值.
21.(2019·山西省长治市第二中学校高二月考)如图,在正方体中,分别是的中点。
(1)求异面直线与所成角的余弦值;
(2)棱上是否存在点,使得平面?请证明你的结论。
【答案】(1);(2)存在点,满足,使得平面;证明见解析
【解析】
以为坐标原点,可建立如下图所示的空间直角坐标系:
设正方体棱长为,则,,,,,,,
(1)设异面直线与所成角为,,
,即异面直线与所成角的余弦值为:
(2)假设在棱上存在点,,使得平面,则,,.设平面的法向量,
,令,则, .
,解得: .棱上存在点,满足,使得平面.
22.(2019·绍兴市教育教学研究院高二期末)如图,平面,,交于点.
(1)证明:;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析(2)
【解析】
(1)证明1:在中,.
因为交于点,所以.
因为平面,
所以,所以.
又因为平面,所以平面
所以平面,所以.
证明2:如图,以为原点,分别以为轴,建立空间直角坐标系.
在中,.因为交于点,所以,所以,
,所以,所以
(2)解:由(1)可知,,.
设平面的法向量为,所以即令,则,所以.设直线与平面所成角为,则.
23.(2019·安徽省高二期中)如图,在四棱锥中,已知平面,且四边形为直角梯形,,,.
(1)求平面与平面所成锐二面角的余弦值;
(2)点是线段上的动点,当直线与所成的角最小时,求线段的长.
【答案】(1) (2)
【解析】以为正交基底建立如图所示的空间直角坐标系,则各点的坐标为.
(1) 因为平面,所以是平面的一个法向量,.因为.设平面的法向量为,则,
即,令,解得.所以是平面的一个法向量,从而,所以平面与平面所成二面角的余弦值为.
(2) 因为,设,
又,则,
又,从而,
设,则,
当且仅当,即时,的最大值为.
因为在上是减函数,此时直线与所成角取得最小值.
又因为,所以.
一、单选题
1.(2020·山东省微山县第二中学高二月考)空间直角坐标中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB与CD的位置关系是( )
A.平行 B.垂直
C.相交但不垂直 D.无法确定
2.(2019·四川省绵阳南山中学高二月考)如图,在平行六面体中,为与的交点若,,,则下列向量中与相等的向量是( )
A. B.
C. D.
3.(2019·江苏省高二期中)已知向量,.若向量与向量平行,则实数的值是( )
A.2 B. C.10 D.
4.(2020·湖南省高二期末)如图,已知正方体ABCD﹣A'B'C'D'中,E是CC'的中点,,,,xyz,则( )
A.x=1,y=2,z=3 B.x,y=1,z=1
C.x=1,y=2,z=2 D.x,y=1,z
5.(2020·四川省双流中学高二月考)正方体不在同一侧面上的两顶点,,则正方体外接球体积是( )
A. B. C. D.
6.(2019·江苏省苏州实验中学高二月考)已知,若点D是AC中点,则( )
A.2 B. C.-3 D.6
7.(2019·江苏省苏州实验中学高二月考)平行六面体中,,则实数x,y,z的值分别为( )
A. B. C. D.
8.(2020·银川唐徕回民中学高二月考)三棱柱中,底面边长和侧棱长都相等,,则异面直线与所成角的余弦值为( )
A. B. C. D.
9.(2019·浙江省柯桥中学高二期中)如图,在三棱柱中,底面,,,则与平面所成角的大小为
A. B. C. D.
10.(2020·山西省高二期末)在一直角坐标系中,已知,现沿轴将坐标平面折成的二面角,则折叠后两点间的距离为( )
A. B. C. D.2
二、多选题
11.(2019·江苏省南京师大附中高二期中)已知点P是平行四边形ABCD所在的平面外一点,如果,,,下列结论正确的有( )
A. B.
C.是平面ABCD的一个法向量 D.
12.(2020·福建省高二期末)在正方体中,,分别是和的中点,则下列结论正确的是( )
A.平面 B.平面
C. D.点与点到平面的距离相等
13.(2020·江苏省启东中学高二开学考试)在正三棱柱中,所有棱长为1,又与交于点,则( )
A.= B.
C.三棱锥的体积为 D.与平面BB′C′C所成的角为
三、填空题
14.(2020·山东省微山县第二中学高二月考)已知向量2,,x,,且,则x的值为______.
15.(2020·河南省高二期末)若向量,,且与的夹角为钝角,则实数的取值范围为________.
16.(2019·山东省济南一中高二期中)如图所示,在正方体中,M为棱的中点,则异面线与AM所成角的余弦值为________.
17.(2019·浙江省杭州高级中学高二期末)如图,四边形和均为正方形,它们所在的平面互相垂直,分别为的中点,则直线与平面所成角的正切值为________;异面直线与所成角的余弦值是________.
四、解答题
18.(2019·包头市第四中学高二期中)如图,已知三棱锥的侧棱两两垂直,且,,是的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线AE和平面OBC的所成角.
19.(2020·盘锦市大洼区高级中学高二期末)如图,在长方体中,,,点、分别为、的中点.
(1)证明:平面;
(2)求二面角的余弦值.
20.(2020·盘锦市大洼区高级中学高二期末)如下图所示,在四棱锥中,底面四边形,四边形是直角梯形,且,,点是棱的中点,是上的点,且.
(1)求异面直线与所成的角的余弦值;
(2)求与平面所成的角的正弦值.
21.(2019·山西省长治市第二中学校高二月考)如图,在正方体中,分别是的中点。
(1)求异面直线与所成角的余弦值;
(2)棱上是否存在点,使得平面?请证明你的结论。
22.(2019·绍兴市教育教学研究院高二期末)如图,平面,,交于点.
(1)证明:;
(2)求直线与平面所成角的正弦值.
23.(2019·安徽省高二期中)如图,在四棱锥中,已知平面,且四边形为直角梯形,,,.
(1)求平面与平面所成锐二面角的余弦值;
(2)点是线段上的动点,当直线与所成的角最小时,求线段的长.
《空间向量与立体几何》单元测试卷答案
一、单选题
1.(2020·山东省微山县第二中学高二月考)空间直角坐标中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB与CD的位置关系是( )
A.平行 B.垂直
C.相交但不垂直 D.无法确定
【答案】A
【解析】
∵空间直角坐标系中,A(1,2,3),B(﹣1,0,5),C(3,0,4),D(4,1,3),
∴=(﹣2,﹣2,2),=(1,1,﹣1),∴=﹣2,∴直线AB与CD平行.故选:A.
2.(2019·四川省绵阳南山中学高二月考)如图,在平行六面体中,为与的交点若,,,则下列向量中与相等的向量是( )
A. B.
C. D.
【答案】A
【解析】如图所示,,,
.故选:A
3.(2019·江苏省高二期中)已知向量,.若向量与向量平行,则实数的值是( )
A.2 B. C.10 D.
【答案】A
【解析】
由已知,,因为与共线,所以存在实数,使得,故
,即,解得.故选:A.
4.(2020·湖南省高二期末)如图,已知正方体ABCD﹣A'B'C'D'中,E是CC'的中点,,,,xyz,则( )
A.x=1,y=2,z=3 B.x,y=1,z=1
C.x=1,y=2,z=2 D.x,y=1,z
【答案】A
【解析】
. 故选:A
5.(2020·四川省双流中学高二月考)正方体不在同一侧面上的两顶点,,则正方体外接球体积是( )
A. B. C. D.
【答案】A
【解析】
容易知:是正方体的体对角线上的两点坐标,
故正方体外接球半径为,故.故选:A.
6.(2019·江苏省苏州实验中学高二月考)已知,若点D是AC中点,则( )
A.2 B. C.-3 D.6
【答案】D
【解析】
,,,.故选:D.
7.(2019·江苏省苏州实验中学高二月考)平行六面体中,,则实数x,y,z的值分别为( )
A. B. C. D.
【答案】C
【解析】
,.故选:C.
8.(2020·银川唐徕回民中学高二月考)三棱柱中,底面边长和侧棱长都相等,,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】B
【解析】
设棱长为1,,,,由题意得:,,.
,,
又,
,
,即异面直线与所成角的余弦值为:
本题正确选项:
9.(2019·浙江省柯桥中学高二期中)如图,在三棱柱中,底面,,,则与平面所成角的大小为
A. B. C. D.
【答案】A
【解析】
取AB的中点D,连接CD,以AD为x轴,以CD为y轴,以为z轴,建立空间直角坐标系,
可得,,故,而,设平面的法向量为,根据,解得,.故与平面所成角的大小为,故选A.
10.(2020·山西省高二期末)在一直角坐标系中,已知,现沿轴将坐标平面折成的二面角,则折叠后两点间的距离为( )
A. B. C. D.2
【答案】D
【解析】
如图为折叠后的图形,其中作
则,
沿轴将坐标平面折成的二面角两异面直线所成的角为.
可得:,故由,得
.故选:D.
二、多选题
11.(2019·江苏省南京师大附中高二期中)已知点P是平行四边形ABCD所在的平面外一点,如果,,,下列结论正确的有( )
A. B.
C.是平面ABCD的一个法向量 D.
【答案】ABC
【解析】
因为,,所以A,B正确,因为所以是平面ABCD的一个法向量,所以C正确,,不满足,则D不正确.故选:ABC.
12.(2020·福建省高二期末)在正方体中,,分别是和的中点,则下列结论正确的是( )
A.平面 B.平面
C. D.点与点到平面的距离相等
【答案】AC
【解析】
对A,因为,分别是和的中点故,故平面成立.对B,建立如图空间直角坐标系,
设正方体边长为2则,.故.故不互相垂直.又属于平面.故平面不成立.对C,同B空间直角坐标系有,.故成立.对D, 点与点到平面的距离相等则点与点中点在平面上.连接易得平面即平面.又点与点中点在上,故点不在平面上.故D不成立. 故选:AC
13.(2020·江苏省启东中学高二开学考试)在正三棱柱中,所有棱长为1,又与交于点,则( )
A.= B.
C.三棱锥的体积为 D.与平面BB′C′C所成的角为
【答案】AC
【解析】
由题意,画出正三棱柱如图所示,
向量,故选项A正确;在中,,,,,所以和不垂直,故选项B错误;在三棱锥中,,点到平面的距离即△中边上的高,所以,所以,故选项C正确;设中点为,所以,又三棱柱是正三棱柱,所以平面,所以即与平面BB′C′C所成的角,,所以,故选项D错误.故选:AC
三、填空题
14.(2020·山东省微山县第二中学高二月考)已知向量2,,x,,且,则x的值为______.
【答案】8
【解析】,解得.
15.(2020·河南省高二期末)若向量,,且与的夹角为钝角,则实数的取值范围为________.
【答案】且
【解析】由与的夹角为钝角可得且与不共线,则即且. 故答案为:且.
16.(2019·山东省济南一中高二期中)如图所示,在正方体中,M为棱的中点,则异面线与AM所成角的余弦值为________.
【答案】
【解析】
分别以的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,
不妨设正方体的棱长为1,则,可得,则,即异面直线与AM所成角的余弦值为. 故答案为:
17.(2019·浙江省杭州高级中学高二期末)如图,四边形和均为正方形,它们所在的平面互相垂直,分别为的中点,则直线与平面所成角的正切值为________;异面直线与所成角的余弦值是________.
【答案】,
【解析】
由两两垂直,分别以所在的直线为轴建立如图所示的空间直角坐标系,设,则,所以,其中平面的一个法向量为,所以与平面所成角的正弦值为,所以;又向量与所成角的余弦值为,又,所以异面直线与所成角的余弦值是.
四、解答题
18.(2019·包头市第四中学高二期中)如图,已知三棱锥的侧棱两两垂直,且,,是的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线AE和平面OBC的所成角.
【答案】(1);(2)
【解析】
建立如图所示的空间直角坐标系,则,,
(1),,故,所以异面直线与所成角的余弦值为.
(2)平面的法向量为,,故,因,故,故与平面所成的角为.
19.(2020·盘锦市大洼区高级中学高二期末)如图,在长方体中,,,点、分别为、的中点.
(1)证明:平面;
(2)求二面角的余弦值.
【答案】(1)见证明;(2)
【解析】
(1)如图,以点A为坐标原点,分别以AB,AD,A为x,y,z轴建立空间直角坐标系
则A(0,0,0),B(1,0,0),D(0,1,0),E(0,0,),(1,1,),,,
,,
与BE是平面BDE内两条相交直线,平面BDE
(2)由(1)进一步可得F(0,),,设平面BDE的法向量为,可取,
设平面FBE的法向量为,,由,可得,取x=1,可得(1,-2,)
. 由于二面角F-BE-D为锐二面角,故所求的二面角的余弦值为
20.(2020·盘锦市大洼区高级中学高二期末)如下图所示,在四棱锥中,底面四边形,四边形是直角梯形,且,,点是棱的中点,是上的点,且.
(1)求异面直线与所成的角的余弦值;
(2)求与平面所成的角的正弦值.
【答案】(1); (2).
【解析】 (1)建系以为原点,如图,,
所以,
(2),,设是平面的法向量,
则,即,取,,所以与平面所成的角的正弦值.
21.(2019·山西省长治市第二中学校高二月考)如图,在正方体中,分别是的中点。
(1)求异面直线与所成角的余弦值;
(2)棱上是否存在点,使得平面?请证明你的结论。
【答案】(1);(2)存在点,满足,使得平面;证明见解析
【解析】
以为坐标原点,可建立如下图所示的空间直角坐标系:
设正方体棱长为,则,,,,,,,
(1)设异面直线与所成角为,,
,即异面直线与所成角的余弦值为:
(2)假设在棱上存在点,,使得平面,则,,.设平面的法向量,
,令,则, .
,解得: .棱上存在点,满足,使得平面.
22.(2019·绍兴市教育教学研究院高二期末)如图,平面,,交于点.
(1)证明:;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析(2)
【解析】
(1)证明1:在中,.
因为交于点,所以.
因为平面,
所以,所以.
又因为平面,所以平面
所以平面,所以.
证明2:如图,以为原点,分别以为轴,建立空间直角坐标系.
在中,.因为交于点,所以,所以,
,所以,所以
(2)解:由(1)可知,,.
设平面的法向量为,所以即令,则,所以.设直线与平面所成角为,则.
23.(2019·安徽省高二期中)如图,在四棱锥中,已知平面,且四边形为直角梯形,,,.
(1)求平面与平面所成锐二面角的余弦值;
(2)点是线段上的动点,当直线与所成的角最小时,求线段的长.
【答案】(1) (2)
【解析】以为正交基底建立如图所示的空间直角坐标系,则各点的坐标为.
(1) 因为平面,所以是平面的一个法向量,.因为.设平面的法向量为,则,
即,令,解得.所以是平面的一个法向量,从而,所以平面与平面所成二面角的余弦值为.
(2) 因为,设,
又,则,
又,从而,
设,则,
当且仅当,即时,的最大值为.
因为在上是减函数,此时直线与所成角取得最小值.
又因为,所以.
