1.3.2 带电粒子在有界磁场中的运动 课件 高二上学期物理人教版(2019)选择性必修第二册(17张PPT)
文档属性
| 名称 | 1.3.2 带电粒子在有界磁场中的运动 课件 高二上学期物理人教版(2019)选择性必修第二册(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-16 16:07:58 | ||
图片预览


文档简介
第一章 安培力与洛伦兹力
1.3-2 带电粒子在匀强磁场中的运动
(有界磁场)
v
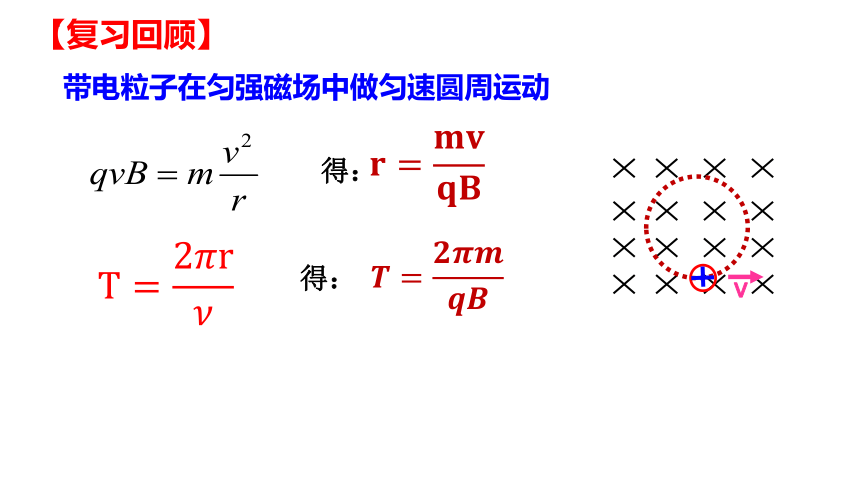
【复习回顾】
????=????????????????
?
得:
????=????????????????????
?
得:
T=2????r????
?
带电粒子在匀强磁场中做匀速圆周运动
v
+q
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
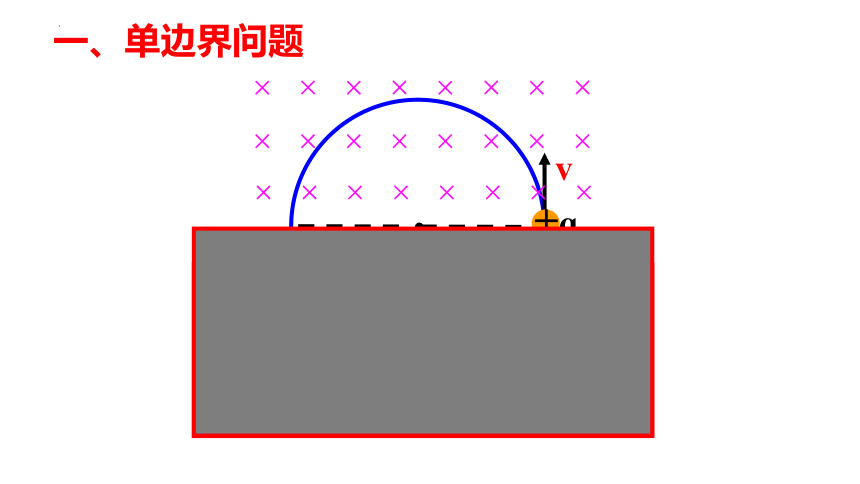
一、单边界问题
v
+q
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
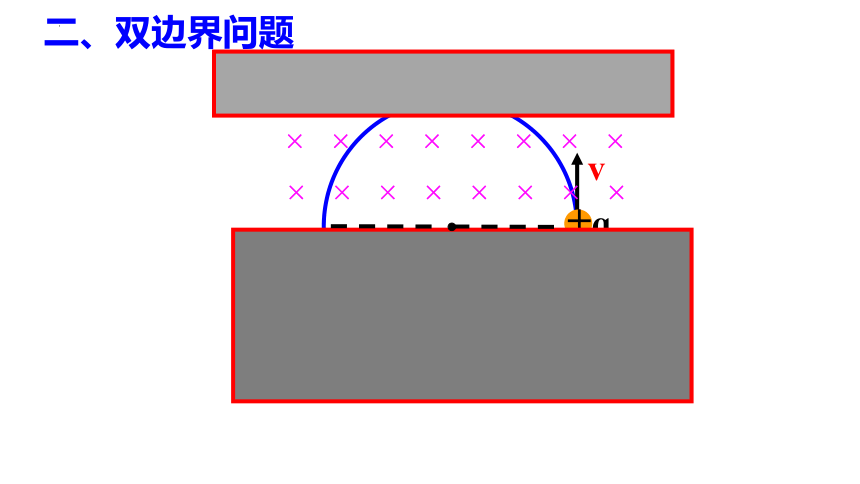
二、双边界问题
【例1】一带正电的粒子以速度v从P点射入匀强磁场并能从ab边界离开磁场。已知带电粒子质量m,电荷量q,磁感应强度B,入射方向与磁场边界ab的夹角为θ 。不计重力。求:
(1)粒子射出磁场的位置与P点的距离;
(2)该粒子在磁场中运动的时间。
Q1:粒子在磁场中受什么力?做什么的运动?
Q2:粒子运动的轨迹是什么样的?
Q3:圆心的位置如何确定?如何求半径 ?
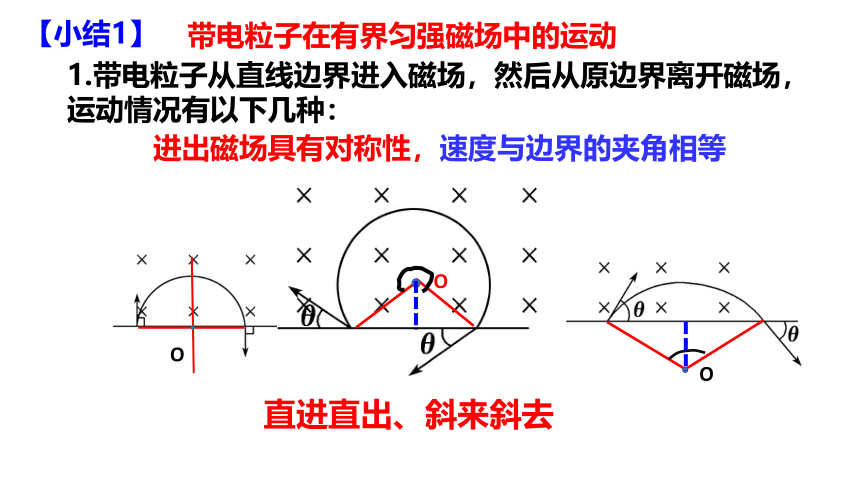
1.带电粒子从直线边界进入磁场,然后从原边界离开磁场,运动情况有以下几种:
进出磁场具有对称性,速度与边界的夹角相等
O
O
O
带电粒子在有界匀强磁场中的运动
直进直出、斜来斜去
【小结1】
d
B
M
θ
v
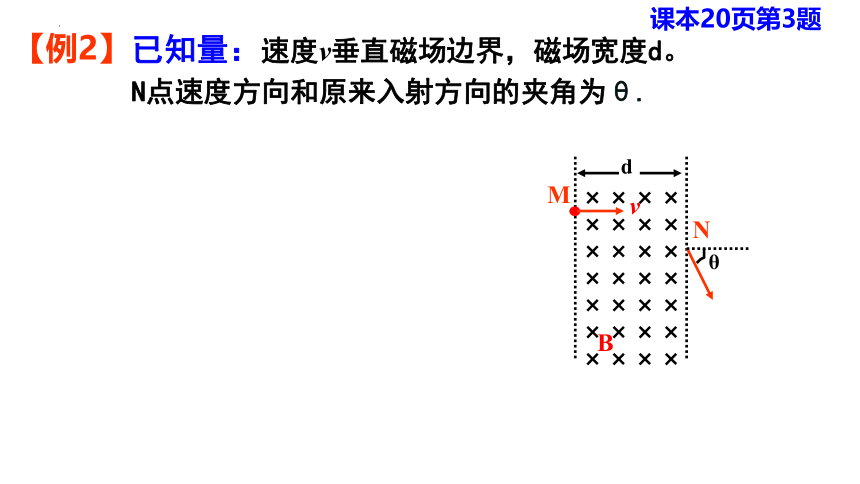
【例2】
已知量:速度v垂直磁场边界,磁场宽度d。
N点速度方向和原来入射方向的夹角为θ.
N
课本20页第3题
带电粒子(不计重力)在磁场中做圆周运动问题的
一般步骤、方法:
2.定圆心(画轨迹)
3.求半径
(1)物理方法:两洛伦兹力延长线的交点为圆心
(2)几何方法:两条速度垂线(半径)的交点;
弦的中垂线与一半径的交点。
(2)几何方法:利用三角函数、勾股定理、圆的知识求r
(1)物理方法:由 得
1.确定入射点和射出点
【小结2】
4.算圆心角,求在磁场运动时间
或
圆心角的大小决定粒子在磁场运动的时间
【练习】质量为m,带电量为-q,不计重力的粒子,从x 轴上的 P (a,0)点以速度大小为 v,沿与 x 轴正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于 y 轴射出第一象限。求:
(1)匀强磁场的磁感应强度B;
(2)带电粒子穿过第一象限所用的时间。
(1) 定圆心。
(2) 定半径。
(3) 定时间。
课本16页第3题
联立解得
又
(1)由几何关系知
【练习】质量为m,带电量为-q,不计重力的粒子,从x 轴上的 P (a,0)点以速度大小为 v,沿与 x 轴正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于 y 轴射出第一象限。求:
(1)匀强磁场的磁感应强度B;(2)带电粒子穿过第一象限所用的时间。
课本16页第3题
r=????????????????????
?
【例3】如图所示,虚线圆所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为 B。一束电子沿圆形区域的直径方向以速度 v 射入磁场,电子束经过磁场区后,其运动方向与原入射方向成 θ 角。设电子质量为 m,电荷量为 e,不计电子之间相互作用力及所受的重力。求: (1) 电子在磁场中运动轨迹的半径 R;
(2) 电子在磁场中运动的时间 t;
(3) 圆形磁场区域的半径 r。
解析: (1) evB = mv2/R
解得 R =mv/eB
(2) 设电子做匀速圆周运动的周期为T,则
T = 2πR/v = 2πm/eB
由如图所示的几何关系得圆心角
α=θ,所以 t = Tα/2π = mθ/eB
(3) 由如图所示几何关系可知,tan= = 所以 r = Rtan
O
3.带电粒子正对磁场的圆心进入圆形磁场区域
当速度沿着磁场半径方向进入磁场时,
粒子一定沿着磁场半径方向射出。
带电粒子在有界匀强磁场中的运动
对着圆心来,
背着圆心去。
【小结4】
1
2
3
带电粒子
在匀强磁场中做匀速圆周的分析方法
圆周运动的圆心
圆周运动的半径
圆周运动的时间
课堂小结
1
2
3
带电粒子在
不同边界磁场中的运动
直线边界
平行边界
圆形边界
(1) 利用 v⊥R
(2) 利用弦的中垂线
(2) 几何法求半径
(1) 向心力公式求半径
直进直出、斜来斜去
存在临界条件
对着圆心来,背着圆心去
2. 平行边界:存在临界条件,如图所示。
带电粒子在有界匀强磁场中的运动
粒子不从右边界飞出
轨迹刚好与边界相切
粒子恰好从边界飞出磁场
粒子的射出点在边缘上
【小结3】
1.3-2 带电粒子在匀强磁场中的运动
(有界磁场)
v
【复习回顾】
????=????????????????
?
得:
????=????????????????????
?
得:
T=2????r????
?
带电粒子在匀强磁场中做匀速圆周运动
v
+q
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
一、单边界问题
v
+q
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
二、双边界问题
【例1】一带正电的粒子以速度v从P点射入匀强磁场并能从ab边界离开磁场。已知带电粒子质量m,电荷量q,磁感应强度B,入射方向与磁场边界ab的夹角为θ 。不计重力。求:
(1)粒子射出磁场的位置与P点的距离;
(2)该粒子在磁场中运动的时间。
Q1:粒子在磁场中受什么力?做什么的运动?
Q2:粒子运动的轨迹是什么样的?
Q3:圆心的位置如何确定?如何求半径 ?
1.带电粒子从直线边界进入磁场,然后从原边界离开磁场,运动情况有以下几种:
进出磁场具有对称性,速度与边界的夹角相等
O
O
O
带电粒子在有界匀强磁场中的运动
直进直出、斜来斜去
【小结1】
d
B
M
θ
v
【例2】
已知量:速度v垂直磁场边界,磁场宽度d。
N点速度方向和原来入射方向的夹角为θ.
N
课本20页第3题
带电粒子(不计重力)在磁场中做圆周运动问题的
一般步骤、方法:
2.定圆心(画轨迹)
3.求半径
(1)物理方法:两洛伦兹力延长线的交点为圆心
(2)几何方法:两条速度垂线(半径)的交点;
弦的中垂线与一半径的交点。
(2)几何方法:利用三角函数、勾股定理、圆的知识求r
(1)物理方法:由 得
1.确定入射点和射出点
【小结2】
4.算圆心角,求在磁场运动时间
或
圆心角的大小决定粒子在磁场运动的时间
【练习】质量为m,带电量为-q,不计重力的粒子,从x 轴上的 P (a,0)点以速度大小为 v,沿与 x 轴正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于 y 轴射出第一象限。求:
(1)匀强磁场的磁感应强度B;
(2)带电粒子穿过第一象限所用的时间。
(1) 定圆心。
(2) 定半径。
(3) 定时间。
课本16页第3题
联立解得
又
(1)由几何关系知
【练习】质量为m,带电量为-q,不计重力的粒子,从x 轴上的 P (a,0)点以速度大小为 v,沿与 x 轴正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于 y 轴射出第一象限。求:
(1)匀强磁场的磁感应强度B;(2)带电粒子穿过第一象限所用的时间。
课本16页第3题
r=????????????????????
?
【例3】如图所示,虚线圆所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为 B。一束电子沿圆形区域的直径方向以速度 v 射入磁场,电子束经过磁场区后,其运动方向与原入射方向成 θ 角。设电子质量为 m,电荷量为 e,不计电子之间相互作用力及所受的重力。求: (1) 电子在磁场中运动轨迹的半径 R;
(2) 电子在磁场中运动的时间 t;
(3) 圆形磁场区域的半径 r。
解析: (1) evB = mv2/R
解得 R =mv/eB
(2) 设电子做匀速圆周运动的周期为T,则
T = 2πR/v = 2πm/eB
由如图所示的几何关系得圆心角
α=θ,所以 t = Tα/2π = mθ/eB
(3) 由如图所示几何关系可知,tan= = 所以 r = Rtan
O
3.带电粒子正对磁场的圆心进入圆形磁场区域
当速度沿着磁场半径方向进入磁场时,
粒子一定沿着磁场半径方向射出。
带电粒子在有界匀强磁场中的运动
对着圆心来,
背着圆心去。
【小结4】
1
2
3
带电粒子
在匀强磁场中做匀速圆周的分析方法
圆周运动的圆心
圆周运动的半径
圆周运动的时间
课堂小结
1
2
3
带电粒子在
不同边界磁场中的运动
直线边界
平行边界
圆形边界
(1) 利用 v⊥R
(2) 利用弦的中垂线
(2) 几何法求半径
(1) 向心力公式求半径
直进直出、斜来斜去
存在临界条件
对着圆心来,背着圆心去
2. 平行边界:存在临界条件,如图所示。
带电粒子在有界匀强磁场中的运动
粒子不从右边界飞出
轨迹刚好与边界相切
粒子恰好从边界飞出磁场
粒子的射出点在边缘上
【小结3】
