人教B版(2019)数学必修第二册5_3_5随机事件的独立性 课时巩固练(含解析)
文档属性
| 名称 | 人教B版(2019)数学必修第二册5_3_5随机事件的独立性 课时巩固练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 66.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览

文档简介
5.3.5 随机事件的独立性
一、常考题型
1.袋内有3个白球和2个黑球,从中不放回地摸球,用A表示“第一次摸得白球”,用B表示“第二次摸得白球”,则A与B是( )
A.互斥事件 B.相互独立事件
C.对立事件 D.不相互独立事件
2.若P(AB)=,P()=,P(B)=,则事件A与B的关系是( )
A.事件A与B互斥 B.事件A与B对立
C.事件A与B相互独立 D.事件A与B既互斥又独立
3.如图,A,B,C表示3个开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么系统的可靠性为( )
A.0.054 B.0.994
C.0.496 D.0.06
4.周老师上数学课时,给班里同学出了两道选择题,她预估做对第一道题的概率为0.80,做对两道题的概率为0.60,则预估做对第二道题的概率是( )
A.0.80 B.0.75
C.0.60 D.0.48
5.设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4,各人是否需使用设备相互独立,则同一工作日至少3人需使用设备的概率为( )
A.0.25 B.0.30
C.0.31 D.0.35
6.有甲、乙两批种子,发芽率分别为0.8和0.9,在两批种子中各取一粒,则恰有一粒种子能发芽的概率是________.
7.在某道路A,B,C三处设有交通灯,这三盏灯在一分钟内开放绿灯的时间分别为25秒、35秒、45秒,某辆车在这条道路上匀速行驶,则三处都不停车的概率为________.
8.某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考三门课程,至少有两门及格为考试通过.
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别为0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.
求:(1)该应聘者用方案一考试通过的概率;
(2)该应聘者用方案二考试通过的概率.
二、易错专项
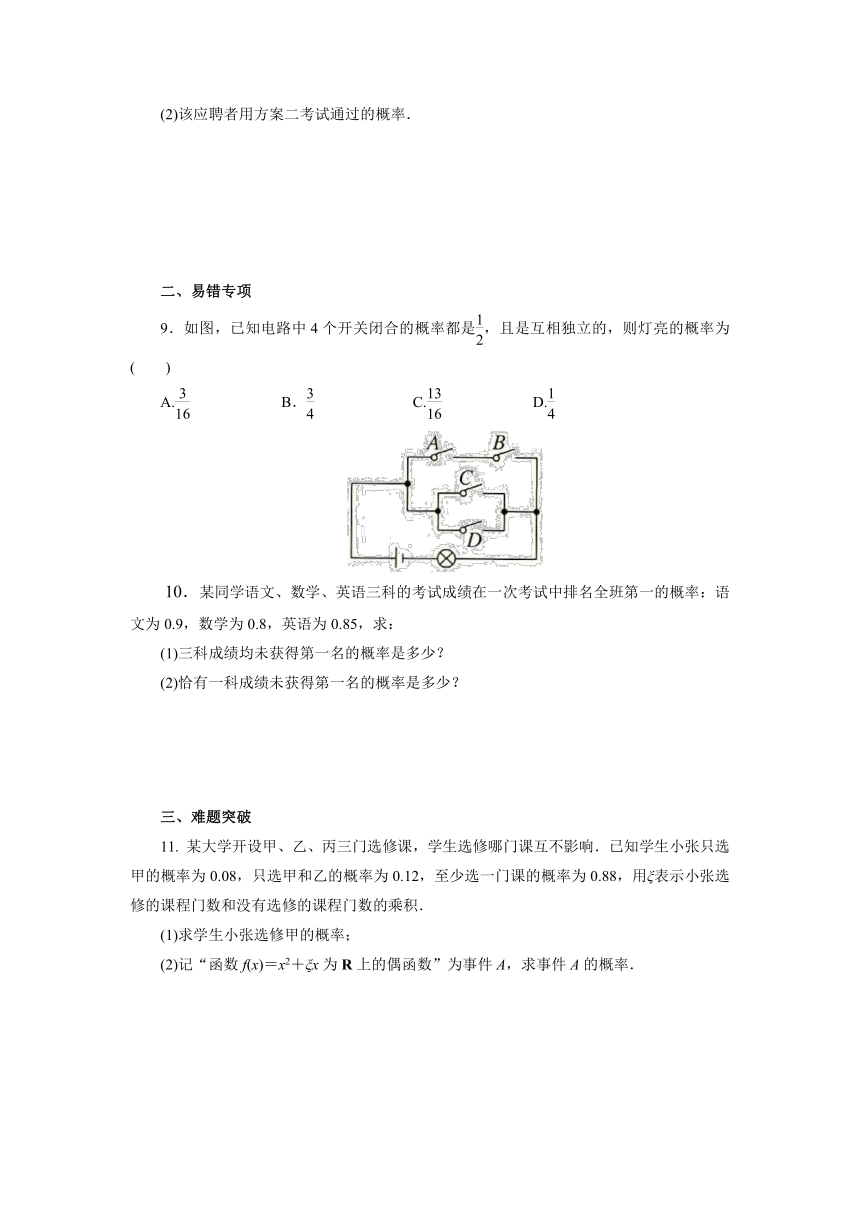
9.如图,已知电路中4个开关闭合的概率都是,且是互相独立的,则灯亮的概率为( )
A. B. C. D.
10.某同学语文、数学、英语三科的考试成绩在一次考试中排名全班第一的概率:语文为0.9,数学为0.8,英语为0.85,求:
(1)三科成绩均未获得第一名的概率是多少?
(2)恰有一科成绩未获得第一名的概率是多少?
三、难题突破
11. 某大学开设甲、乙、丙三门选修课,学生选修哪门课互不影响.已知学生小张只选甲的概率为0.08,只选甲和乙的概率为0.12,至少选一门课的概率为0.88,用ξ表示小张选修的课程门数和没有选修的课程门数的乘积.
(1)求学生小张选修甲的概率;
(2)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率.
参考答案
1.D
解析:根据互斥事件、对立事件和相互独立事件的定义可知,A与B不是相互独立事件.故选D.
2.C
解析:因为P()=,
所以P(A)=,又P(B)=,P(AB)=,
所以有P(AB)=P(A)P(B),
所以事件A与B相互独立但不一定互斥.
故选C.
3. B
解析:记三个开关都正常工作分别为事件A,B,C,
则P(A)=0.9,P(B)=0.8,P(C)=0.7.
三个开关同时出现故障的事件为∩∩,
则此系统正常工作的概率为
P=1-P( )=1-P()P()P()=1-0.1×0.2×0.3=0.994.
故选B.
4.B
解析:设“做对第一道题”为事件A,“做对第二道题”为事件B,
则P(AB)=P(A)P(B)=0.8×P(B)=0.6,
故P(B)=0.75.
故选B.
5.C
解析:设甲、乙、丙、丁需使用设备分别为事件A,B,C,D,
则P(A)=0.6,P(B)=P(C)=0.5,P(D)=0.4,
恰好3人使用设备的概率
P1=P(BCD∪ACD∪ABD∪ABC)
=(1-0.6)×0.5×0.5×0.4+0.6×(1-0.5)×0.5×0.4+0.6×0.5×(1-0.5)×0.4+0.6×0.5×0.5×(1-0.4)
=0.25,
4人使用设备的概率P2=P(ABCD)=0.6×0.5×0.5×0.4=0.06,
故所求概率P=P1+P2=0.25+0.06=0.31.
故选C.
6.答案:0.26
解析:所求概率P=0.8×0.1+0.2×0.9=0.26.
7.答案:
解析:由题意可知,每个交通灯开放绿灯的概率分别为,,.
在这个道路上匀速行驶,则三处都不停车的概率为××=.
8.解:记该应聘者对三门指定课程考试及格的事件分别为A,B,C,
则P(A)=0.5,P(B)=0.6,P(C)=0.9.
(1)应聘者用方案一考试通过的概率为
P1=P(AB)+P(BC)+P(AC)+P(ABC)
=0.5×0.6×0.1+0.5×0.6×0.9+0.5×0.4×0.9+0.5×0.6×0.9
=0.75.
(2)应聘者用方案二考试通过的概率为
P2=P(AB)+P(BC)+P(AC)
=×0.5×0.6+×0.6×0.9+×0.5×0.9
=0.43.
9.C
解析:记“A,B,C,D四个开关闭合”分别为事件A,B,C,D,
可用对立事件求解,
图中含开关的三条线路同时断开的概率为:
P()P()[1-P(AB)]=××=.
所以灯亮的概率为1-=.
故选C.
10.解:分别记该生语文、数学、英语考试成绩排名全班第一的事件为A,B,C,
则A,B,C两两相互独立且P(A)=0.9,P(B)=0.8,P(C)=0.85.
(1)“三科成绩均未获得第一名”可以用 表示,
所求的概率为
P( )=P()P()P()
=[1-P(A)][1-P(B)][1-P(C)]
=(1-0.9)(1-0.8)(1-0.85)
=0.003,
即三科成绩均未获得第一名的概率是0.003.
(2)“恰有一科成绩未获得第一名”可以用(BC)∪(AC)∪(AB)表示.
由于事件BC,AC和AB两两互斥,
根据概率的加法公式和事件独立性定义,
所求的概率为
P(BC)+P(AC)+P(AB)
=P()P(B)P(C)+P(A)P()P(C)+P(A)P(B)P()
=[1-P(A)]P(B)P(C)+P(A)[1-P(B)]P(C)+P(A)P(B)[1-P(C)]
=(1-0.9)×0.8×0.85+0.9×(1-0.8)×0.85+0.9×0.8×(1-0.85)=0.329,
即恰有一科成绩未获得第一名的概率是0.329.
11. 解:(1)设学生小张选修甲、乙、丙的概率分别为x,y,z,
则解得
所以学生小张选修甲的概率为0.4.
(2)若函数f(x)=x2+ξx为R上的偶函数,
则ξ=0,当ξ=0时,表示小张选修三门课或三门课都不选.
所以
P(A)=P(ξ=0)
=xyz+(1-x)(1-y)(1-z)
=0.4×0.6×0.5+(1-0.4)(1-0.6)(1-0.5)
=0.24,
即事件A的概率为0.24.
一、常考题型
1.袋内有3个白球和2个黑球,从中不放回地摸球,用A表示“第一次摸得白球”,用B表示“第二次摸得白球”,则A与B是( )
A.互斥事件 B.相互独立事件
C.对立事件 D.不相互独立事件
2.若P(AB)=,P()=,P(B)=,则事件A与B的关系是( )
A.事件A与B互斥 B.事件A与B对立
C.事件A与B相互独立 D.事件A与B既互斥又独立
3.如图,A,B,C表示3个开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么系统的可靠性为( )
A.0.054 B.0.994
C.0.496 D.0.06
4.周老师上数学课时,给班里同学出了两道选择题,她预估做对第一道题的概率为0.80,做对两道题的概率为0.60,则预估做对第二道题的概率是( )
A.0.80 B.0.75
C.0.60 D.0.48
5.设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4,各人是否需使用设备相互独立,则同一工作日至少3人需使用设备的概率为( )
A.0.25 B.0.30
C.0.31 D.0.35
6.有甲、乙两批种子,发芽率分别为0.8和0.9,在两批种子中各取一粒,则恰有一粒种子能发芽的概率是________.
7.在某道路A,B,C三处设有交通灯,这三盏灯在一分钟内开放绿灯的时间分别为25秒、35秒、45秒,某辆车在这条道路上匀速行驶,则三处都不停车的概率为________.
8.某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考三门课程,至少有两门及格为考试通过.
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别为0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.
求:(1)该应聘者用方案一考试通过的概率;
(2)该应聘者用方案二考试通过的概率.
二、易错专项
9.如图,已知电路中4个开关闭合的概率都是,且是互相独立的,则灯亮的概率为( )
A. B. C. D.
10.某同学语文、数学、英语三科的考试成绩在一次考试中排名全班第一的概率:语文为0.9,数学为0.8,英语为0.85,求:
(1)三科成绩均未获得第一名的概率是多少?
(2)恰有一科成绩未获得第一名的概率是多少?
三、难题突破
11. 某大学开设甲、乙、丙三门选修课,学生选修哪门课互不影响.已知学生小张只选甲的概率为0.08,只选甲和乙的概率为0.12,至少选一门课的概率为0.88,用ξ表示小张选修的课程门数和没有选修的课程门数的乘积.
(1)求学生小张选修甲的概率;
(2)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率.
参考答案
1.D
解析:根据互斥事件、对立事件和相互独立事件的定义可知,A与B不是相互独立事件.故选D.
2.C
解析:因为P()=,
所以P(A)=,又P(B)=,P(AB)=,
所以有P(AB)=P(A)P(B),
所以事件A与B相互独立但不一定互斥.
故选C.
3. B
解析:记三个开关都正常工作分别为事件A,B,C,
则P(A)=0.9,P(B)=0.8,P(C)=0.7.
三个开关同时出现故障的事件为∩∩,
则此系统正常工作的概率为
P=1-P( )=1-P()P()P()=1-0.1×0.2×0.3=0.994.
故选B.
4.B
解析:设“做对第一道题”为事件A,“做对第二道题”为事件B,
则P(AB)=P(A)P(B)=0.8×P(B)=0.6,
故P(B)=0.75.
故选B.
5.C
解析:设甲、乙、丙、丁需使用设备分别为事件A,B,C,D,
则P(A)=0.6,P(B)=P(C)=0.5,P(D)=0.4,
恰好3人使用设备的概率
P1=P(BCD∪ACD∪ABD∪ABC)
=(1-0.6)×0.5×0.5×0.4+0.6×(1-0.5)×0.5×0.4+0.6×0.5×(1-0.5)×0.4+0.6×0.5×0.5×(1-0.4)
=0.25,
4人使用设备的概率P2=P(ABCD)=0.6×0.5×0.5×0.4=0.06,
故所求概率P=P1+P2=0.25+0.06=0.31.
故选C.
6.答案:0.26
解析:所求概率P=0.8×0.1+0.2×0.9=0.26.
7.答案:
解析:由题意可知,每个交通灯开放绿灯的概率分别为,,.
在这个道路上匀速行驶,则三处都不停车的概率为××=.
8.解:记该应聘者对三门指定课程考试及格的事件分别为A,B,C,
则P(A)=0.5,P(B)=0.6,P(C)=0.9.
(1)应聘者用方案一考试通过的概率为
P1=P(AB)+P(BC)+P(AC)+P(ABC)
=0.5×0.6×0.1+0.5×0.6×0.9+0.5×0.4×0.9+0.5×0.6×0.9
=0.75.
(2)应聘者用方案二考试通过的概率为
P2=P(AB)+P(BC)+P(AC)
=×0.5×0.6+×0.6×0.9+×0.5×0.9
=0.43.
9.C
解析:记“A,B,C,D四个开关闭合”分别为事件A,B,C,D,
可用对立事件求解,
图中含开关的三条线路同时断开的概率为:
P()P()[1-P(AB)]=××=.
所以灯亮的概率为1-=.
故选C.
10.解:分别记该生语文、数学、英语考试成绩排名全班第一的事件为A,B,C,
则A,B,C两两相互独立且P(A)=0.9,P(B)=0.8,P(C)=0.85.
(1)“三科成绩均未获得第一名”可以用 表示,
所求的概率为
P( )=P()P()P()
=[1-P(A)][1-P(B)][1-P(C)]
=(1-0.9)(1-0.8)(1-0.85)
=0.003,
即三科成绩均未获得第一名的概率是0.003.
(2)“恰有一科成绩未获得第一名”可以用(BC)∪(AC)∪(AB)表示.
由于事件BC,AC和AB两两互斥,
根据概率的加法公式和事件独立性定义,
所求的概率为
P(BC)+P(AC)+P(AB)
=P()P(B)P(C)+P(A)P()P(C)+P(A)P(B)P()
=[1-P(A)]P(B)P(C)+P(A)[1-P(B)]P(C)+P(A)P(B)[1-P(C)]
=(1-0.9)×0.8×0.85+0.9×(1-0.8)×0.85+0.9×0.8×(1-0.85)=0.329,
即恰有一科成绩未获得第一名的概率是0.329.
11. 解:(1)设学生小张选修甲、乙、丙的概率分别为x,y,z,
则解得
所以学生小张选修甲的概率为0.4.
(2)若函数f(x)=x2+ξx为R上的偶函数,
则ξ=0,当ξ=0时,表示小张选修三门课或三门课都不选.
所以
P(A)=P(ξ=0)
=xyz+(1-x)(1-y)(1-z)
=0.4×0.6×0.5+(1-0.4)(1-0.6)(1-0.5)
=0.24,
即事件A的概率为0.24.
