人教B版(2019)数学必修第二册6_3_1向量在平面几何中的应用 课时精练(含解析)
文档属性
| 名称 | 人教B版(2019)数学必修第二册6_3_1向量在平面几何中的应用 课时精练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 80.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览

文档简介
6.3.1向量在平面几何中的应用
一、常考题型
1.在△ABC中,若(+)·(-)=0,则△ABC( )
A.是正三角形 B.是直角三角形
C.是等腰三角形 D.形状无法确定
2.在四边形ABCD中,=(1,2),=(-4,2),则该四边形的面积为( )
A. B.2 C.5 D.10
3.在直角三角形ABC中,斜边BC长为2,O是平面ABC内一点,点P满足=+(+),则||等于( )
A.2 B.1 C. D.4
4.(多选)△ABC是边长为2的等边三角形,已知向量a,b满足=2a,=2a+b,则下列结论正确的是( )
A.|b|=1 B.|a|=1
C.a∥b D.(4a+b)⊥
5.设O为△ABC的外心,平面上一点P使=++,则点P是△ABC的( )
A.外心 B.内心
C.垂心 D.重心
6.已知A,B,C三点不在同一条直线上,O是平面ABC内一定点,P是△ABC内的一动点,若-=λ,λ∈[0,+∞),则直线AP一定过△ABC的( )
A.重心 B.垂心
C.外心 D.内心
7.在四边形ABCD中,已知=(4,-2),=(7,4),=(3,6),则四边形ABCD的面积是 .
8.如图,在△OAB中,已知点P为线段AB上的一点,且||=2||.
(1)试用、表示;
(2)若||=3,||=2,且∠AOB=,求·的值.
二、易错专项
9.向量a≠e,|e|=1,若对任意t∈R,|a-te|≥|a+e|,则( C )
A.a⊥e B.a⊥(a+e)
C.e⊥(a+e) D.(a+e)⊥(a-e)
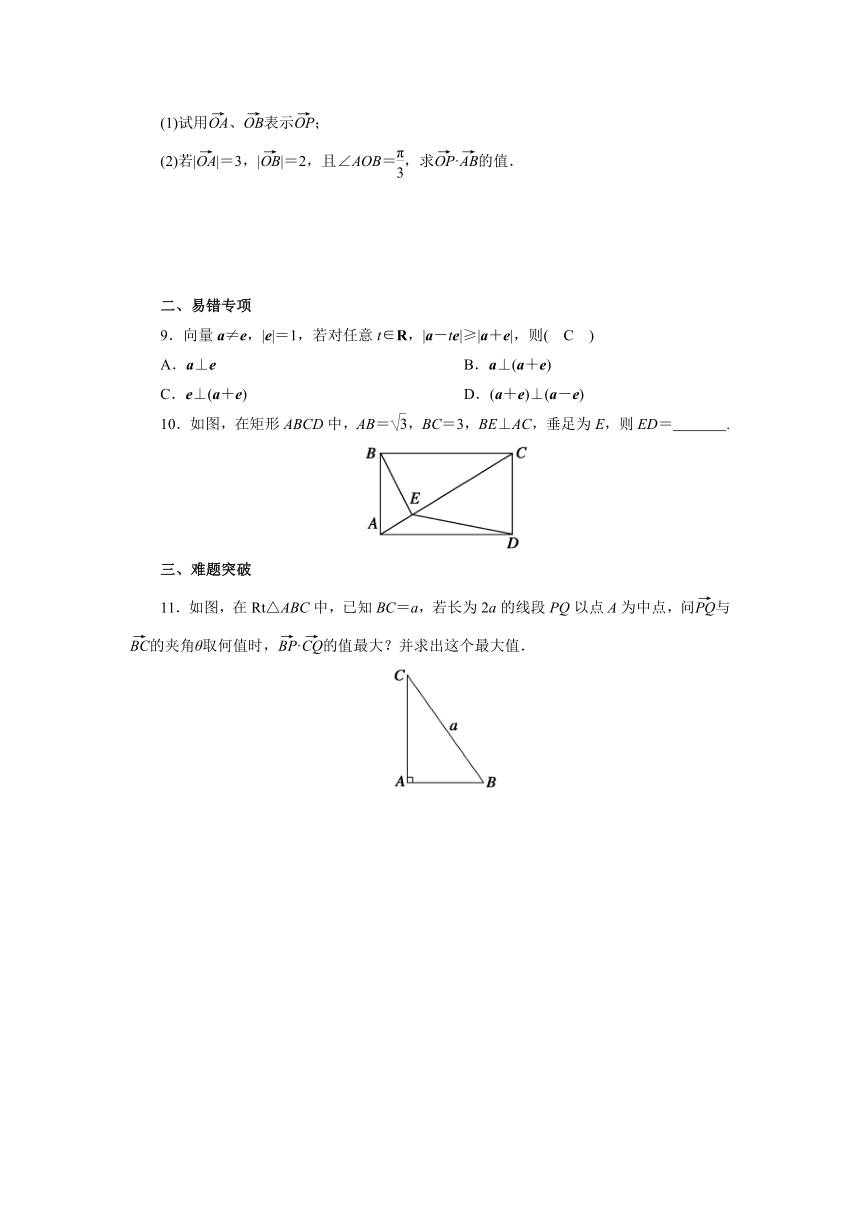
10.如图,在矩形ABCD中,AB=,BC=3,BE⊥AC,垂足为E,则ED= .
三、难题突破
11.如图,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问与的夹角θ取何值时,·的值最大?并求出这个最大值.
参考答案
1.答案:C
解析:由条件知2=2,即||=||,即△ABC为等腰三角形.
2.答案:C
解析:因为·=(1,2)×(-4,2)=1×(-4)+2×2=0,所以⊥,且||==,||==2,所以S四边形ABCD=||||=××2=5.故选C.
3.答案:B
解析:设BC边的中点为M,则(+)=,
∴=+=,∴P与M重合,
∴||=||=1.
4.答案:BD
解析:如图,由题意,=-=(2a+b)-2a=b,则|b|=2,A错误;
|2a|=2|a|=2,所以|a|=1,B正确;
因为=2a,=b,故a,b不平行,C错误;
设BC的中点为D,则+=2,且⊥,而2=2a+(2a+b)=4a+b,所以(4a+b)⊥,D正确.
5.答案:C
解析:由=++,得=+,以OB,OC为邻边作 OBDC,如图.
∵O为△ABC的外心,∴OB=OC.
∴四边形OBDC为菱形.
∴OD⊥BC.
又=+=,∴AP⊥BC.
同理,BP⊥AC.故P为垂心.
6.答案:A
解析:如图,取BC的中点D,
则+=+=.
又∵-=λ,
∴=λ,
∴A,P,D三点共线,
∴直线AP一定过△ABC的重心
7.答案:30.
解析:=-=(3,6)=,
因为·=(4,-2)×(3,6)=0,
所以四边形ABCD为矩形,
因为||==2,
||==3,
所以S四边形ABCD=||||=2×3=30.
8.解:(1)因为点P在AB上,且||=2||,所以=2,
即-=2(-),所以=+.
(2)·=(+)·(-)
=-2+2-·
=-||2+||2-||·||cos∠AOB
=-×9+×4-×3×2cos=-.
9.答案:C
解析:由|a-te|≥|a+e|得(a-te)2≥(a+e)2,
故t2-2a·et-(2a·e+1)≥0.
∵对任意t∈R,上式恒成立,
∴Δ=4(a·e)2+4(2a·e+1)≤0.∴(a·e+1)2≤0.
∴a·e=-1,∴e·(a+e)=a·e+1=0,∴e⊥(a+e).
10.答案:.
解析:以A为坐标原点,AD,AB所在直线分别为x轴,y轴建立平面直角坐标系,则A(0,0),B(0,),C(3,),
D(3,0),=(3,),设=λ,则E的坐标为(3λ,λ),故=(3λ,λ-).因为BE⊥AC,所以·=0,
即9λ+3λ-3=0,解得λ=,所以E(,).
故=(,-),||=,即ED=.
11.解: 以直角顶点A为坐标原点,两直角边所在直线为坐标轴建立平面直角坐标系.设|AB|=c,|AC|=b,则A(0,0),B(c,0),C(0,b),且|PQ|=2a,|BC|=a.
设点P的坐标为(x,y),则Q(-x,-y),∴=(x-c,y),=(-x,-y-b),=(-c,b),=(-2x,-2y).
∴·=(x-c)(-x)+y(-y-b)=-(x2+y2)+cx-by.
∵cosθ==,∴cx-by=a2cosθ.
∴·=-a2+a2cosθ,
故当cosθ=1,即θ=0°(与方向相同)时,·最大,其最大值为0.
一、常考题型
1.在△ABC中,若(+)·(-)=0,则△ABC( )
A.是正三角形 B.是直角三角形
C.是等腰三角形 D.形状无法确定
2.在四边形ABCD中,=(1,2),=(-4,2),则该四边形的面积为( )
A. B.2 C.5 D.10
3.在直角三角形ABC中,斜边BC长为2,O是平面ABC内一点,点P满足=+(+),则||等于( )
A.2 B.1 C. D.4
4.(多选)△ABC是边长为2的等边三角形,已知向量a,b满足=2a,=2a+b,则下列结论正确的是( )
A.|b|=1 B.|a|=1
C.a∥b D.(4a+b)⊥
5.设O为△ABC的外心,平面上一点P使=++,则点P是△ABC的( )
A.外心 B.内心
C.垂心 D.重心
6.已知A,B,C三点不在同一条直线上,O是平面ABC内一定点,P是△ABC内的一动点,若-=λ,λ∈[0,+∞),则直线AP一定过△ABC的( )
A.重心 B.垂心
C.外心 D.内心
7.在四边形ABCD中,已知=(4,-2),=(7,4),=(3,6),则四边形ABCD的面积是 .
8.如图,在△OAB中,已知点P为线段AB上的一点,且||=2||.
(1)试用、表示;
(2)若||=3,||=2,且∠AOB=,求·的值.
二、易错专项
9.向量a≠e,|e|=1,若对任意t∈R,|a-te|≥|a+e|,则( C )
A.a⊥e B.a⊥(a+e)
C.e⊥(a+e) D.(a+e)⊥(a-e)
10.如图,在矩形ABCD中,AB=,BC=3,BE⊥AC,垂足为E,则ED= .
三、难题突破
11.如图,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问与的夹角θ取何值时,·的值最大?并求出这个最大值.
参考答案
1.答案:C
解析:由条件知2=2,即||=||,即△ABC为等腰三角形.
2.答案:C
解析:因为·=(1,2)×(-4,2)=1×(-4)+2×2=0,所以⊥,且||==,||==2,所以S四边形ABCD=||||=××2=5.故选C.
3.答案:B
解析:设BC边的中点为M,则(+)=,
∴=+=,∴P与M重合,
∴||=||=1.
4.答案:BD
解析:如图,由题意,=-=(2a+b)-2a=b,则|b|=2,A错误;
|2a|=2|a|=2,所以|a|=1,B正确;
因为=2a,=b,故a,b不平行,C错误;
设BC的中点为D,则+=2,且⊥,而2=2a+(2a+b)=4a+b,所以(4a+b)⊥,D正确.
5.答案:C
解析:由=++,得=+,以OB,OC为邻边作 OBDC,如图.
∵O为△ABC的外心,∴OB=OC.
∴四边形OBDC为菱形.
∴OD⊥BC.
又=+=,∴AP⊥BC.
同理,BP⊥AC.故P为垂心.
6.答案:A
解析:如图,取BC的中点D,
则+=+=.
又∵-=λ,
∴=λ,
∴A,P,D三点共线,
∴直线AP一定过△ABC的重心
7.答案:30.
解析:=-=(3,6)=,
因为·=(4,-2)×(3,6)=0,
所以四边形ABCD为矩形,
因为||==2,
||==3,
所以S四边形ABCD=||||=2×3=30.
8.解:(1)因为点P在AB上,且||=2||,所以=2,
即-=2(-),所以=+.
(2)·=(+)·(-)
=-2+2-·
=-||2+||2-||·||cos∠AOB
=-×9+×4-×3×2cos=-.
9.答案:C
解析:由|a-te|≥|a+e|得(a-te)2≥(a+e)2,
故t2-2a·et-(2a·e+1)≥0.
∵对任意t∈R,上式恒成立,
∴Δ=4(a·e)2+4(2a·e+1)≤0.∴(a·e+1)2≤0.
∴a·e=-1,∴e·(a+e)=a·e+1=0,∴e⊥(a+e).
10.答案:.
解析:以A为坐标原点,AD,AB所在直线分别为x轴,y轴建立平面直角坐标系,则A(0,0),B(0,),C(3,),
D(3,0),=(3,),设=λ,则E的坐标为(3λ,λ),故=(3λ,λ-).因为BE⊥AC,所以·=0,
即9λ+3λ-3=0,解得λ=,所以E(,).
故=(,-),||=,即ED=.
11.解: 以直角顶点A为坐标原点,两直角边所在直线为坐标轴建立平面直角坐标系.设|AB|=c,|AC|=b,则A(0,0),B(c,0),C(0,b),且|PQ|=2a,|BC|=a.
设点P的坐标为(x,y),则Q(-x,-y),∴=(x-c,y),=(-x,-y-b),=(-c,b),=(-2x,-2y).
∴·=(x-c)(-x)+y(-y-b)=-(x2+y2)+cx-by.
∵cosθ==,∴cx-by=a2cosθ.
∴·=-a2+a2cosθ,
故当cosθ=1,即θ=0°(与方向相同)时,·最大,其最大值为0.
