人教版 八年级上册 因式分解 完全平方公式 优质课件(共15张PPT)
文档属性
| 名称 | 人教版 八年级上册 因式分解 完全平方公式 优质课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 740.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 12:36:58 | ||
图片预览




文档简介
(共15张PPT)
14.3.2 因式分解
—公式法(2)
在数学的天地里,
重要的不是我们知道什么,
而是我们应该怎样知道。
1. 通过拼图了解完全平方公式的几何意义;
2. 能识别完全平方式,掌握完全平方公式的形式和特征;
3. 会运用完全平方公式进行简单的分解因式;
4. 能综合运用因式分解的基本方法进行因式分解.
学习目标
1.分解因式的定义:
温故知新:
=m(a+b+c)
2.分解因式的方法:
ma+mb+mc
a2- b2
=(a+b)(a-b)
提公因式法
平方差公式法
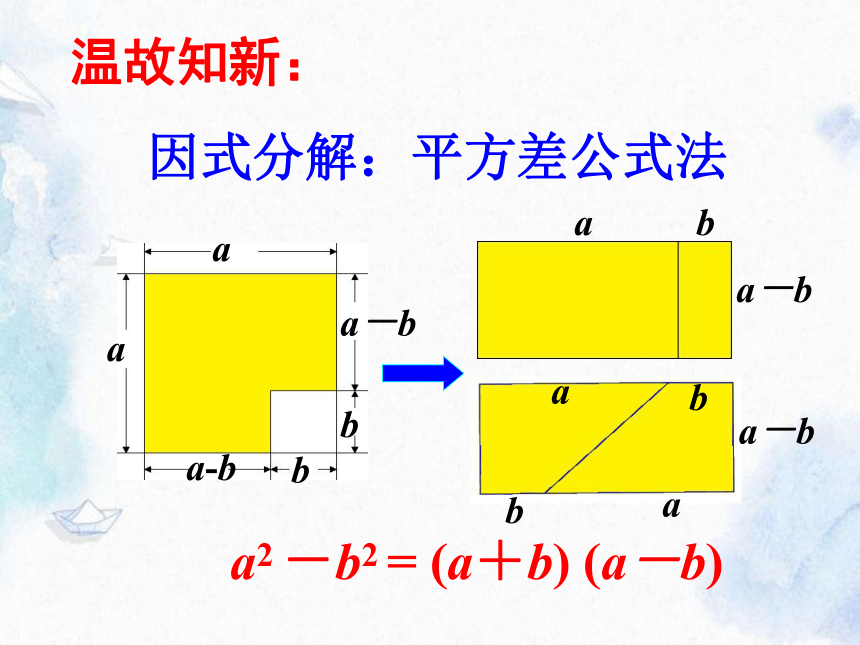
a2 -b2 = (a+b) (a-b)
a
b
b
a-b
a-b
a
a
a
a
a-b
a-b
b
b
b
因式分解:平方差公式法
温故知新:
温故知新:
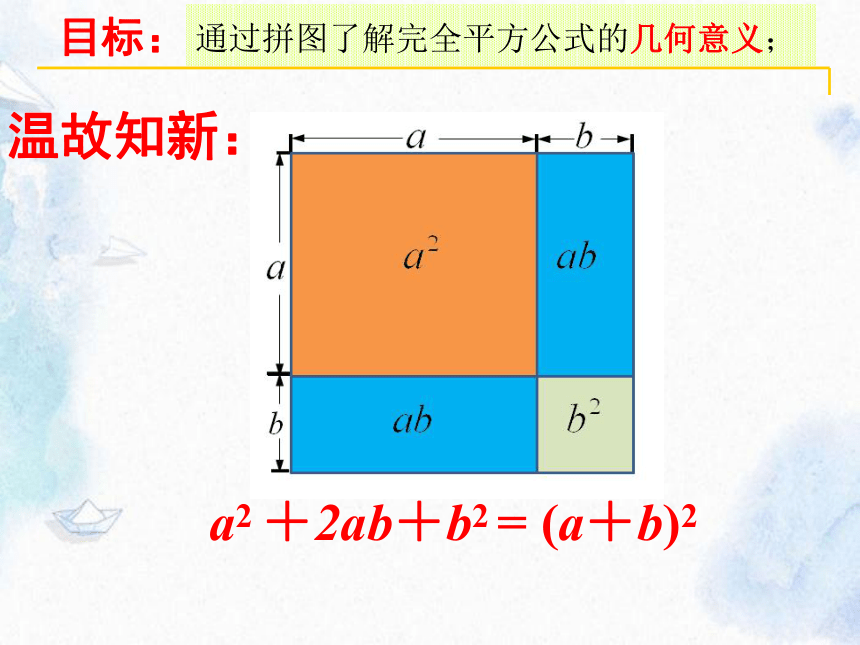
a2 +2ab+b2 = (a+b)2
通过拼图了解完全平方公式的几何意义;
目标:
温故知新:
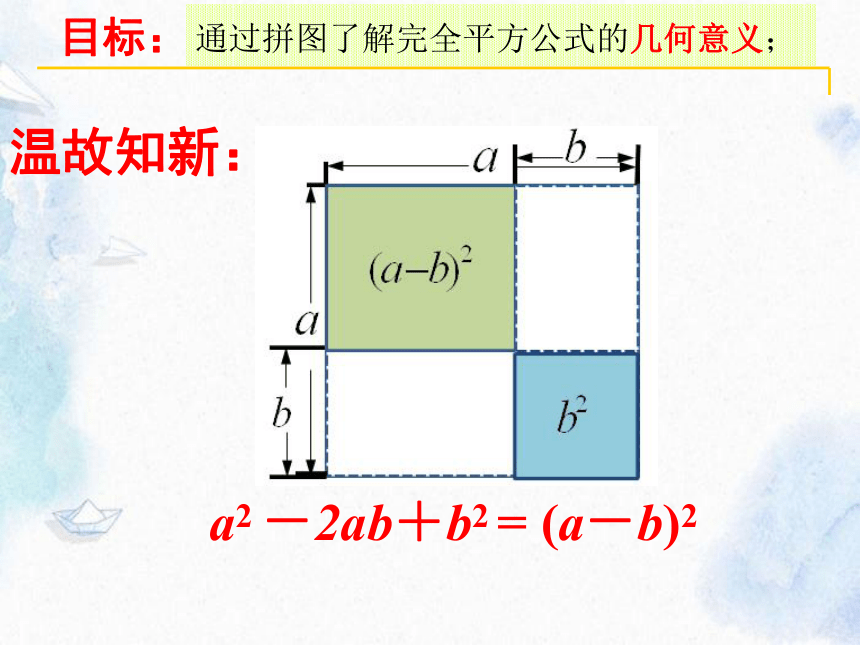
a2 -2ab+b2 = (a-b)2
通过拼图了解完全平方公式的几何意义;
目标:
因式分解:
整式乘法:
(a±b)2
a2±2ab+b2
=
=
(a±b)2
a2±2ab+b2
两个数的平方和,加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
对比与思考:
掌握完全平方公式的形式和特征;
目标:
能用完全平方公式分解因式的多项式的特征:
1.由三项组成;
2.有两项可以写成两个数的平方和的形式;
3.另一项是这两个数乘积的2倍.
能识别完全平方式;
目标:
(1) a2-4a+4 (2) 1+4a2
(3) 4b2+4b-1 (4) a2+ab+b2
(5) (6)9a2-6a+1
下列多项式能否用完全平方公式分解因式?说说你的理由.
能识别完全平方式;
目标:
a2+2ab+b2 =(a + b)2
分解因式:
(1) x2 -12x+36=x2- ·x· +( )2
= (x - )2
x2 +2·x·3+32
(x + 3)2
=
(2) 16x2 +24x+9=( )2+2·( )·( )+( )2
= ( + )2
掌握完全平方公式的形式和特征;
目标:
把下列各式分解因式:
(1) -x2+4xy-4y2
(2) (a+b)2 -12(a+b)+36
会运用完全平方公式进行简单的分解因式;
目标:
(3) 3ax2+6axy + 3ay2
请同学们设计能用上完全平方公式分解因式的题目,请其他同学作出解答你再给予评价.
2
2
=
(
)
+
± 2
±
2
把下列各式分解因式:
(2) (a2 + 1)2 -4a2
能综合运用因式分解的基本方法进行因式分解;
目标:
(1) a4-2a2+1
思考:
1. 使用完全平方公式分解因式的步骤.
2.分解因式的注意事项
a、b可以是什么式子呢?
小结与思考:
a2 ±2ab+b2 = (a±b)2
课本第119习题14.3(3、5)
14.3.2 因式分解
—公式法(2)
在数学的天地里,
重要的不是我们知道什么,
而是我们应该怎样知道。
1. 通过拼图了解完全平方公式的几何意义;
2. 能识别完全平方式,掌握完全平方公式的形式和特征;
3. 会运用完全平方公式进行简单的分解因式;
4. 能综合运用因式分解的基本方法进行因式分解.
学习目标
1.分解因式的定义:
温故知新:
=m(a+b+c)
2.分解因式的方法:
ma+mb+mc
a2- b2
=(a+b)(a-b)
提公因式法
平方差公式法
a2 -b2 = (a+b) (a-b)
a
b
b
a-b
a-b
a
a
a
a
a-b
a-b
b
b
b
因式分解:平方差公式法
温故知新:
温故知新:
a2 +2ab+b2 = (a+b)2
通过拼图了解完全平方公式的几何意义;
目标:
温故知新:
a2 -2ab+b2 = (a-b)2
通过拼图了解完全平方公式的几何意义;
目标:
因式分解:
整式乘法:
(a±b)2
a2±2ab+b2
=
=
(a±b)2
a2±2ab+b2
两个数的平方和,加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
对比与思考:
掌握完全平方公式的形式和特征;
目标:
能用完全平方公式分解因式的多项式的特征:
1.由三项组成;
2.有两项可以写成两个数的平方和的形式;
3.另一项是这两个数乘积的2倍.
能识别完全平方式;
目标:
(1) a2-4a+4 (2) 1+4a2
(3) 4b2+4b-1 (4) a2+ab+b2
(5) (6)9a2-6a+1
下列多项式能否用完全平方公式分解因式?说说你的理由.
能识别完全平方式;
目标:
a2+2ab+b2 =(a + b)2
分解因式:
(1) x2 -12x+36=x2- ·x· +( )2
= (x - )2
x2 +2·x·3+32
(x + 3)2
=
(2) 16x2 +24x+9=( )2+2·( )·( )+( )2
= ( + )2
掌握完全平方公式的形式和特征;
目标:
把下列各式分解因式:
(1) -x2+4xy-4y2
(2) (a+b)2 -12(a+b)+36
会运用完全平方公式进行简单的分解因式;
目标:
(3) 3ax2+6axy + 3ay2
请同学们设计能用上完全平方公式分解因式的题目,请其他同学作出解答你再给予评价.
2
2
=
(
)
+
± 2
±
2
把下列各式分解因式:
(2) (a2 + 1)2 -4a2
能综合运用因式分解的基本方法进行因式分解;
目标:
(1) a4-2a2+1
思考:
1. 使用完全平方公式分解因式的步骤.
2.分解因式的注意事项
a、b可以是什么式子呢?
小结与思考:
a2 ±2ab+b2 = (a±b)2
课本第119习题14.3(3、5)
