人教版 八年级上册 平方差公式 公开 课件(共22张PPT)
文档属性
| 名称 | 人教版 八年级上册 平方差公式 公开 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 900.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 13:17:48 | ||
图片预览





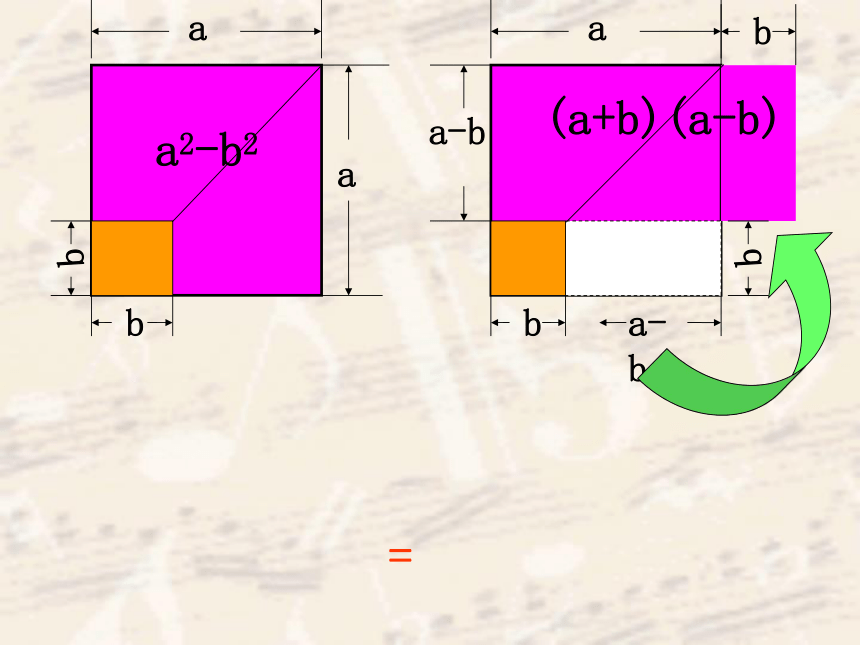

文档简介
(共22张PPT)
八年级上册14.2.1
平方差公式
14.2乘法公式
14.2.1平方差公式
学习目标:
1.经历探索平方差公式的过程,会推导平方差公式。
2.理解探索平方差公式的几何意义。
3.理解平方差公式的结构特征,灵活应用平方差公式。
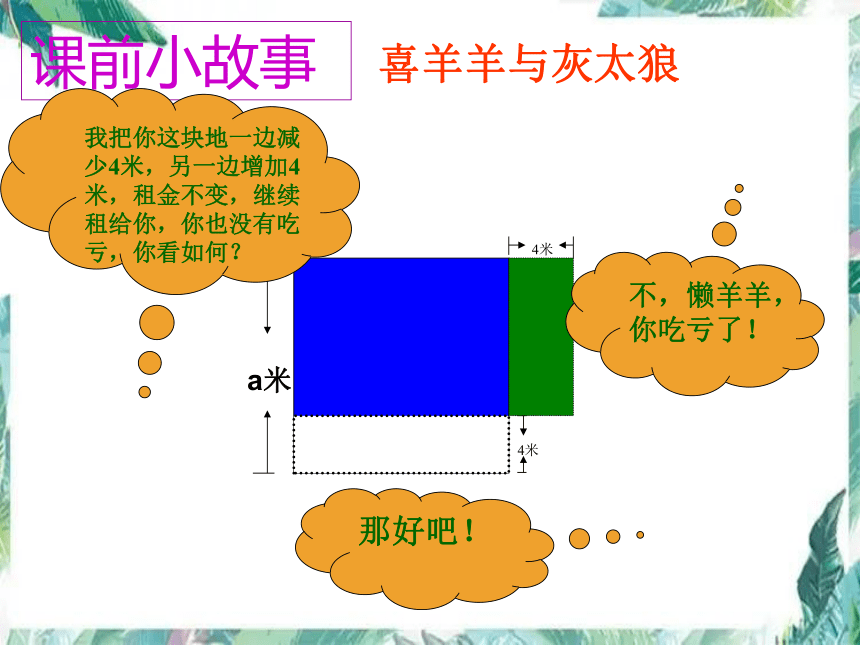
喜羊羊与灰太狼
课前小故事
4米
4米
a米
我把你这块地一边减少4米,另一边增加4米,租金不变,继续租给你,你也没有吃亏,你看如何?
不,懒羊羊,你吃亏了!
那好吧!
(x + 2)( x+8)
=x2
+8x
+2X
+16
=x2
+10x
多项式与多项式是如何相乘的?
+16
(a+b) (m+n)
=am
+an
+bm
+bn
探究1
①(x + 3)( x-3)
②(1 + 2a)( 1-2a)
③(4m+ n)( 4m-n)
先观察相乘的两个多项式有什么共同点?再计算。
这些等式的结果什么特点?你能用一句话概括这些等式吗?
两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式
(a+b)(a-b) = a2-b2
这个公式叫做(乘法的)平方差公式.
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
=
a-b
a-b
小组交流:
请根据你对平方差公式的理解,写两个多项式乘多项式,先小组内讨论能否用平方差公式,如果不能,为什么?如果能,请说出答案。
写一写,考考你!
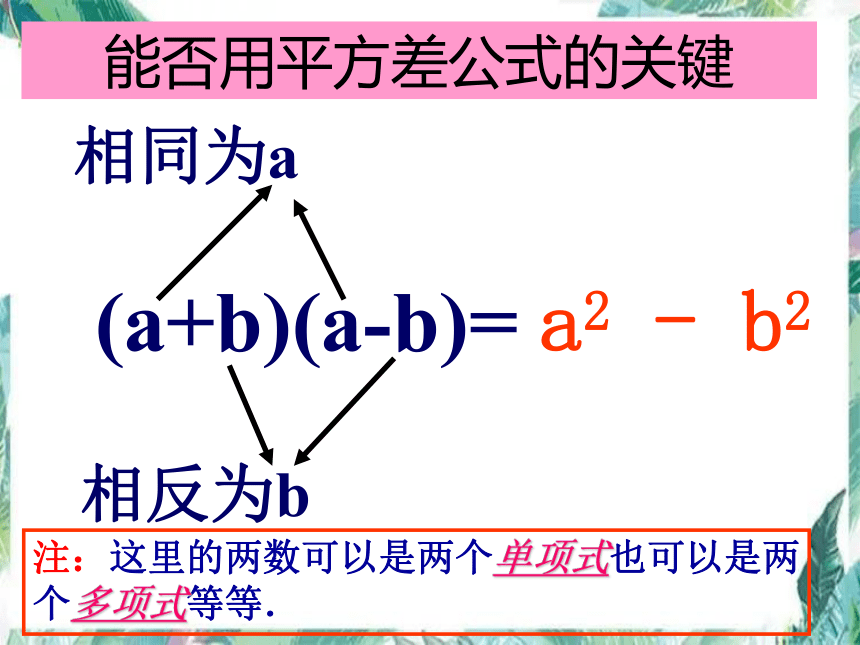
(a+b)(a-b)= a2 - b2
相同为a
相反为b
能否用平方差公式的关键
注:这里的两数可以是两个单项式也可以是两个多项式等等.
(1) ( 2 a+b)( 2a b)
(2) (m n) (n m)
(3) (5x+2) (2x-5)
(4) (a+b+c)(a+b-c)
(5) (m 3n)(m+3n)
(能)
(不能)
(不能)
(能)
活动一
1.判断下列式子能否用平方差公式计算.
(能)
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
2.找一找、填一填
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
(a + b ) ( a – b ) = a2 - b2
例1、用平方差公式计算
(1)(3x+2y)(3x-2y)
注意
1、先把要计算的式子与公式对照,
2、哪个是 a
哪个是 b
活动二
法一
利用加法交换律,
变成公式标准形式.
法二
提取两“ ”号中的“ ”号,变成公式标准形式.
(2) ( 3x 5)(3x 5)
例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .
(a+b)(a-b)= a2 - b2
对于不符合平方差公式标准形式者,可以利用加法交换律,或提取两“ ”号中的“ ”号,或拆项,变成公式标准形式后,再用公式.
平方差公式的运用
(3)51×49
相信自己 我能行!
利用平方差公式计算:
(4)(x+4) (x 4) (2x +3) (3x 2)
(1)(3+2a)(-3+2a)
(2)(-8x-y)(-8x+y)
1.化简
拓展提升:
2.计算:
(1+1/2)(1+1/4)(1+1/16)
拓展提升:
(a+b)(a b)=a2 b2.
对于不符合平方差公式标准形式者,或提取两“ ”号中的“ ”号,利用加法交换律,或拆项,变成公式标准形式后,再用公式.
平方差公式
课堂小结
两个数的和与这两个数的差的积,等于这两个数的平方差.
4米
4米
a米
(a-4)
(a+4)米
原来
现在
a2
(a+4)(a-4)
我会做:
1 . 利用平方差公式计算:
(1)(6+3a)( 6 + 3a)
(2)501×499
(3)(2m+4) (2m 4) (5m +6) (6m 5)
2.计算
(1+1/3)(1+1/9)(1+1/81)
给我最大快乐的,不是已懂的知识,
而是不断的学习.----高斯
八年级上册14.2.1
平方差公式
14.2乘法公式
14.2.1平方差公式
学习目标:
1.经历探索平方差公式的过程,会推导平方差公式。
2.理解探索平方差公式的几何意义。
3.理解平方差公式的结构特征,灵活应用平方差公式。
喜羊羊与灰太狼
课前小故事
4米
4米
a米
我把你这块地一边减少4米,另一边增加4米,租金不变,继续租给你,你也没有吃亏,你看如何?
不,懒羊羊,你吃亏了!
那好吧!
(x + 2)( x+8)
=x2
+8x
+2X
+16
=x2
+10x
多项式与多项式是如何相乘的?
+16
(a+b) (m+n)
=am
+an
+bm
+bn
探究1
①(x + 3)( x-3)
②(1 + 2a)( 1-2a)
③(4m+ n)( 4m-n)
先观察相乘的两个多项式有什么共同点?再计算。
这些等式的结果什么特点?你能用一句话概括这些等式吗?
两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式
(a+b)(a-b) = a2-b2
这个公式叫做(乘法的)平方差公式.
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
=
a-b
a-b
小组交流:
请根据你对平方差公式的理解,写两个多项式乘多项式,先小组内讨论能否用平方差公式,如果不能,为什么?如果能,请说出答案。
写一写,考考你!
(a+b)(a-b)= a2 - b2
相同为a
相反为b
能否用平方差公式的关键
注:这里的两数可以是两个单项式也可以是两个多项式等等.
(1) ( 2 a+b)( 2a b)
(2) (m n) (n m)
(3) (5x+2) (2x-5)
(4) (a+b+c)(a+b-c)
(5) (m 3n)(m+3n)
(能)
(不能)
(不能)
(能)
活动一
1.判断下列式子能否用平方差公式计算.
(能)
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
2.找一找、填一填
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
(a + b ) ( a – b ) = a2 - b2
例1、用平方差公式计算
(1)(3x+2y)(3x-2y)
注意
1、先把要计算的式子与公式对照,
2、哪个是 a
哪个是 b
活动二
法一
利用加法交换律,
变成公式标准形式.
法二
提取两“ ”号中的“ ”号,变成公式标准形式.
(2) ( 3x 5)(3x 5)
例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .
(a+b)(a-b)= a2 - b2
对于不符合平方差公式标准形式者,可以利用加法交换律,或提取两“ ”号中的“ ”号,或拆项,变成公式标准形式后,再用公式.
平方差公式的运用
(3)51×49
相信自己 我能行!
利用平方差公式计算:
(4)(x+4) (x 4) (2x +3) (3x 2)
(1)(3+2a)(-3+2a)
(2)(-8x-y)(-8x+y)
1.化简
拓展提升:
2.计算:
(1+1/2)(1+1/4)(1+1/16)
拓展提升:
(a+b)(a b)=a2 b2.
对于不符合平方差公式标准形式者,或提取两“ ”号中的“ ”号,利用加法交换律,或拆项,变成公式标准形式后,再用公式.
平方差公式
课堂小结
两个数的和与这两个数的差的积,等于这两个数的平方差.
4米
4米
a米
(a-4)
(a+4)米
原来
现在
a2
(a+4)(a-4)
我会做:
1 . 利用平方差公式计算:
(1)(6+3a)( 6 + 3a)
(2)501×499
(3)(2m+4) (2m 4) (5m +6) (6m 5)
2.计算
(1+1/3)(1+1/9)(1+1/81)
给我最大快乐的,不是已懂的知识,
而是不断的学习.----高斯
