人教版 八年级上册 平方差公式 公开课 课件(共15张PPT)
文档属性
| 名称 | 人教版 八年级上册 平方差公式 公开课 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 606.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 13:18:44 | ||
图片预览






文档简介
(共15张PPT)
1、会推导平方差公式,并能用公式进行简单的运算。
2、理解掌握平方差公式的结构特征,并能灵活熟练的运用平方差公式。
学习目标:
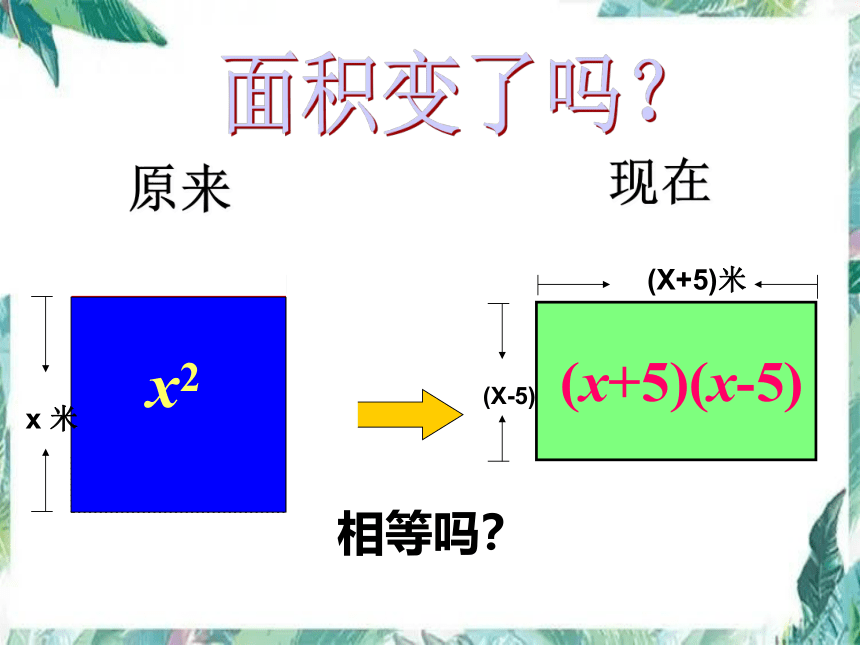
从前有一个狡猾的地主,他把一块边长为x米的正方形的土地租给张老汉种植,有一天,他对张老汉说:“ 我把这块地的一边减少5米,另一边增加5米,继续租给你,你也没有吃亏,你看如何?” 聪明的同学们,你觉得这个买卖公平吗?
情景引入:
5米
5米
x 米
(X-5)
(X+5)米
相等吗?
原来
现在
x2
(x+5)(x-5)
=(2x)2 -6x +6x-32
=m2 -2m +2m-22
=x2 -x +x-12
(m+ 2)( m-2)
(2x + 3)(2x-3)
(x + 1)( x-1)
1、它们的结果有什么特点?
两个数的平方差
2、算式有什么特点?
两个数的和乘以两个数的差
3、能不能用字母表示你的发现?
(a+b)(a-b)=a2-b2
-x +x
-6x +6x
-12
-2m +2m
-22
-32
探究新知:
平方差公式:
(a+b)(a b)=a2 b2
两个数的和与这两个数的差的积, 等于这两个数的平方差。
温馨提示:公式中的a和b,既可以是具体的数,也可以是单项式或者多项式。
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
1、找一找、填一填
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
例1、运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ; (2) (-x+2y)(-x-2y).
解:(1)(3x+2)(3x-2)
=(3x)2-22
=9x2-4;
(2) (-x+2y)(-x-2y)
=(-x)2-(2y)2
= x2-4y2
a
使用平方差公式(a+b)(a-b)=a -b 时,关键在于找准___与___,公式左边积的两个因式中相同的项看作a,互为相反数的项中带正号的项看作b。
如:
(2x+3y)(3y-2x)中,____看作a,____看作b.
b
3y
2x
例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1) 102×98
(y+2)(y-2)- (y-1)(y+5)
= 1002-22
=1000 – 4
=(100+2)(100-2)
=9996
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
( )
化简
(x4+y4 )
(x4+y4 )
(x4+y4)
拓展提升
5.化简:(2+1)(22+1)(24+1)(28+1)(216+1)+1
原式= (2+1)(22+1)(24+1)(28+1)(216+1)+1
= 1×(2+1)(22+1)(24+1)(28+1)(216+1)+1
=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)+1
= (22-1)(24+1)(28+1)(216+1)+1
= 232-1+1
= 232
【解析】
放鞭炮:
(a+b)(a-b)=(a)2-(b)2
相反为b
课堂小结
相同为a
适当交换
合理加括号
相同数的平方减去相反数的平方
平方差公式
P153 练习1、2
P156 习题15.2 第1题
1、会推导平方差公式,并能用公式进行简单的运算。
2、理解掌握平方差公式的结构特征,并能灵活熟练的运用平方差公式。
学习目标:
从前有一个狡猾的地主,他把一块边长为x米的正方形的土地租给张老汉种植,有一天,他对张老汉说:“ 我把这块地的一边减少5米,另一边增加5米,继续租给你,你也没有吃亏,你看如何?” 聪明的同学们,你觉得这个买卖公平吗?
情景引入:
5米
5米
x 米
(X-5)
(X+5)米
相等吗?
原来
现在
x2
(x+5)(x-5)
=(2x)2 -6x +6x-32
=m2 -2m +2m-22
=x2 -x +x-12
(m+ 2)( m-2)
(2x + 3)(2x-3)
(x + 1)( x-1)
1、它们的结果有什么特点?
两个数的平方差
2、算式有什么特点?
两个数的和乘以两个数的差
3、能不能用字母表示你的发现?
(a+b)(a-b)=a2-b2
-x +x
-6x +6x
-12
-2m +2m
-22
-32
探究新知:
平方差公式:
(a+b)(a b)=a2 b2
两个数的和与这两个数的差的积, 等于这两个数的平方差。
温馨提示:公式中的a和b,既可以是具体的数,也可以是单项式或者多项式。
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
1、找一找、填一填
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
例1、运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ; (2) (-x+2y)(-x-2y).
解:(1)(3x+2)(3x-2)
=(3x)2-22
=9x2-4;
(2) (-x+2y)(-x-2y)
=(-x)2-(2y)2
= x2-4y2
a
使用平方差公式(a+b)(a-b)=a -b 时,关键在于找准___与___,公式左边积的两个因式中相同的项看作a,互为相反数的项中带正号的项看作b。
如:
(2x+3y)(3y-2x)中,____看作a,____看作b.
b
3y
2x
例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1) 102×98
(y+2)(y-2)- (y-1)(y+5)
= 1002-22
=1000 – 4
=(100+2)(100-2)
=9996
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
( )
化简
(x4+y4 )
(x4+y4 )
(x4+y4)
拓展提升
5.化简:(2+1)(22+1)(24+1)(28+1)(216+1)+1
原式= (2+1)(22+1)(24+1)(28+1)(216+1)+1
= 1×(2+1)(22+1)(24+1)(28+1)(216+1)+1
=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)+1
= (22-1)(24+1)(28+1)(216+1)+1
= 232-1+1
= 232
【解析】
放鞭炮:
(a+b)(a-b)=(a)2-(b)2
相反为b
课堂小结
相同为a
适当交换
合理加括号
相同数的平方减去相反数的平方
平方差公式
P153 练习1、2
P156 习题15.2 第1题
