人教版数学 八年级上册 因式分解平方差公式 课件(共16张PPT)
文档属性
| 名称 | 人教版数学 八年级上册 因式分解平方差公式 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 500.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
14.3.2公式法(1)
—用平方差公式分解因式
和老师比比,你能快速算出下面(1)-(3)题吗?
速算游戏
(1)322-312
(2) 592-412
8
15
(
)
2
7
15
(
)
2
-
(3)
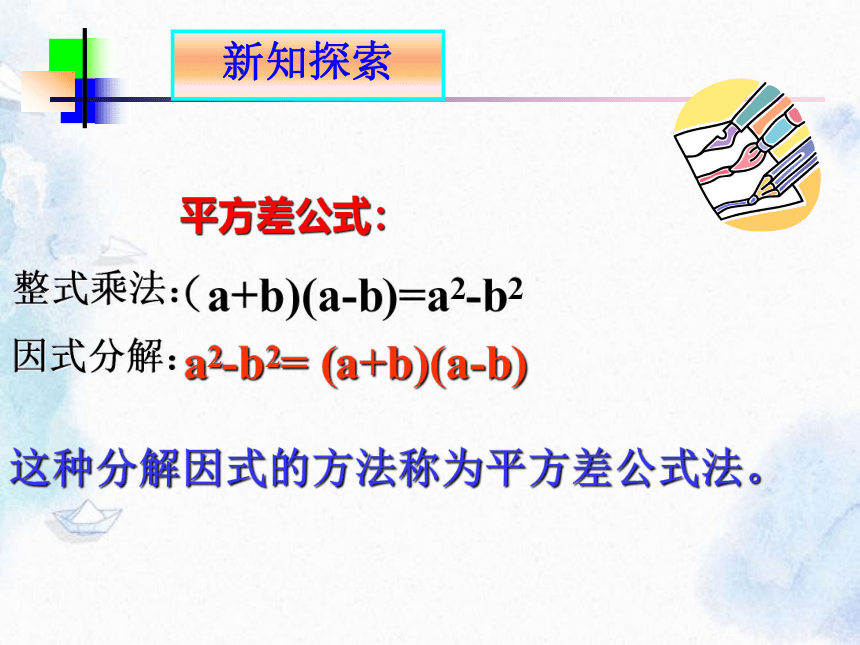
新知探索
平方差公式:
(a+b)(a-b)=a2-b2
整式乘法:
因式分解:
这种分解因式的方法称为平方差公式法。
a2-b2= (a+b)(a-b)
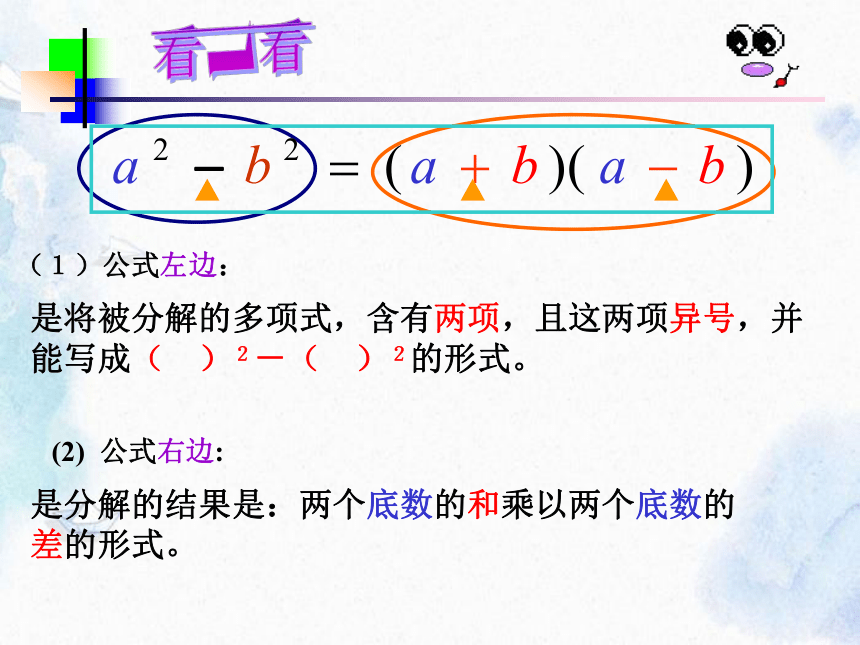
看一看
(1)公式左边:
是将被分解的多项式,含有两项,且这两项异号,并能写成( )2-( )2的形式。
(2) 公式右边:
是分解的结果是:两个底数的和乘以两个底数的差的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
试一试,你能行!
下列多项式能化成()2-()2的形式吗?
若能,请将其化成()2-()2形式
(1) 4m2 -1
(4)-x2 -25y2
(2)4m2+9
(3)x2 -25y 2
(5) -x2+25y2
= ( 4m)2 -(1)2
不能转化为平方差形式
不能转化为平方差形式
= x2 -(5y)2
= 25y2-x2 =(5y)2 -x2
a2 - b2= (a + b) (a - b)
铺路之石
填空:
(1) =( )2 ; (2) 0.81=( )2;
(3)9m2 = ( )2; (4) 25a2b2=( )2;
(5) 4(a-b)2=[ ]2;
(6) (x+y)2=[ ]2。
首页
上页
下页
1
36
1
16
1
4
± (x+y)
± 0.9
± 3m
± 5ab
± 2(a-b)
1
6
±
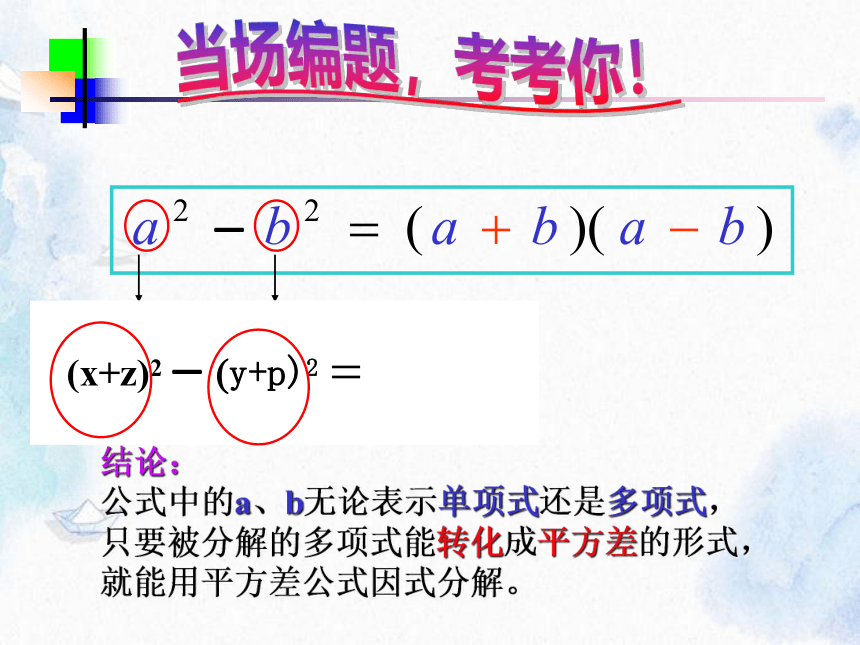
当场编题,考考你!
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
20062-20052 =
(2mn)2 - ( 3xy)2 =
(x+z)2 - (y+p)2 =
结论:
公式中的a、b无论表示单项式还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解。
应用举例
在使用平方差公式分解因式时要 注意:
先把要分解的多项式与平方差公式对照,
明确哪个相当于 a , 哪个相当于 b.
例1:把下列各式分解因式:
(1)
(2)(x+y)2-z2
小试牛刀(1)
针对性练习:把下列各式分解因式
例2、分解因式
(1)-16a2+9b2
(2) 9(a+b)2-4(a-b)2
小试牛刀 2
把下列各式分解因式:
① 0.25m2n2 – 1
② 25(x+y)2 - 16(x-y)2
活学活用
活学活用
1、利用因式分解速算:582-422
挑战提升:
不信难不倒你!
2、用你学过的方法分解因式:
(1)4x3 - 9xy2
及时归纳:
分解因式步骤:一提二套
注意:多项式因式分解要分解到不能再分解 为止。
(2) x4-y4
=x(4x2-9y2)
=x(2x+3y)(2x-3y)
=(x2+y2)(x2-y2)
= (x2+y2 )(x+y)(x-y)
谈谈你的收获
a2 - b2=(a+b)(a - b)
小结:
考考你
你知道992-1能否被100整除吗?
说说你是怎么想的?
如图,为某小区绿化带设计图
问:你能快速算出此环形绿地面积吗?
解决实际问题
14.3.2公式法(1)
—用平方差公式分解因式
和老师比比,你能快速算出下面(1)-(3)题吗?
速算游戏
(1)322-312
(2) 592-412
8
15
(
)
2
7
15
(
)
2
-
(3)
新知探索
平方差公式:
(a+b)(a-b)=a2-b2
整式乘法:
因式分解:
这种分解因式的方法称为平方差公式法。
a2-b2= (a+b)(a-b)
看一看
(1)公式左边:
是将被分解的多项式,含有两项,且这两项异号,并能写成( )2-( )2的形式。
(2) 公式右边:
是分解的结果是:两个底数的和乘以两个底数的差的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
试一试,你能行!
下列多项式能化成()2-()2的形式吗?
若能,请将其化成()2-()2形式
(1) 4m2 -1
(4)-x2 -25y2
(2)4m2+9
(3)x2 -25y 2
(5) -x2+25y2
= ( 4m)2 -(1)2
不能转化为平方差形式
不能转化为平方差形式
= x2 -(5y)2
= 25y2-x2 =(5y)2 -x2
a2 - b2= (a + b) (a - b)
铺路之石
填空:
(1) =( )2 ; (2) 0.81=( )2;
(3)9m2 = ( )2; (4) 25a2b2=( )2;
(5) 4(a-b)2=[ ]2;
(6) (x+y)2=[ ]2。
首页
上页
下页
1
36
1
16
1
4
± (x+y)
± 0.9
± 3m
± 5ab
± 2(a-b)
1
6
±
当场编题,考考你!
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
20062-20052 =
(2mn)2 - ( 3xy)2 =
(x+z)2 - (y+p)2 =
结论:
公式中的a、b无论表示单项式还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解。
应用举例
在使用平方差公式分解因式时要 注意:
先把要分解的多项式与平方差公式对照,
明确哪个相当于 a , 哪个相当于 b.
例1:把下列各式分解因式:
(1)
(2)(x+y)2-z2
小试牛刀(1)
针对性练习:把下列各式分解因式
例2、分解因式
(1)-16a2+9b2
(2) 9(a+b)2-4(a-b)2
小试牛刀 2
把下列各式分解因式:
① 0.25m2n2 – 1
② 25(x+y)2 - 16(x-y)2
活学活用
活学活用
1、利用因式分解速算:582-422
挑战提升:
不信难不倒你!
2、用你学过的方法分解因式:
(1)4x3 - 9xy2
及时归纳:
分解因式步骤:一提二套
注意:多项式因式分解要分解到不能再分解 为止。
(2) x4-y4
=x(4x2-9y2)
=x(2x+3y)(2x-3y)
=(x2+y2)(x2-y2)
= (x2+y2 )(x+y)(x-y)
谈谈你的收获
a2 - b2=(a+b)(a - b)
小结:
考考你
你知道992-1能否被100整除吗?
说说你是怎么想的?
如图,为某小区绿化带设计图
问:你能快速算出此环形绿地面积吗?
解决实际问题
