人教版 八年级上册数学 平方差公式 优质课件(共13张PPT)
文档属性
| 名称 | 人教版 八年级上册数学 平方差公式 优质课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
14.2.1平方差公式
人教版 八年级上册数学
环节设置
复习引入
归纳新知
几何意义
例题分析
计算下列各式:
【问题1】观察这三个运算及运算结果,你能发现等式两边的式子各有什么特点吗?
总结收获
?
平方差公式:
=
【问题2】请你用学过的知识对上述猜想进行验证.
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
【归纳】
两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式:
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
【问题3】你能将这个公式用文字语言进行表述吗?
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
平方差公式:
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
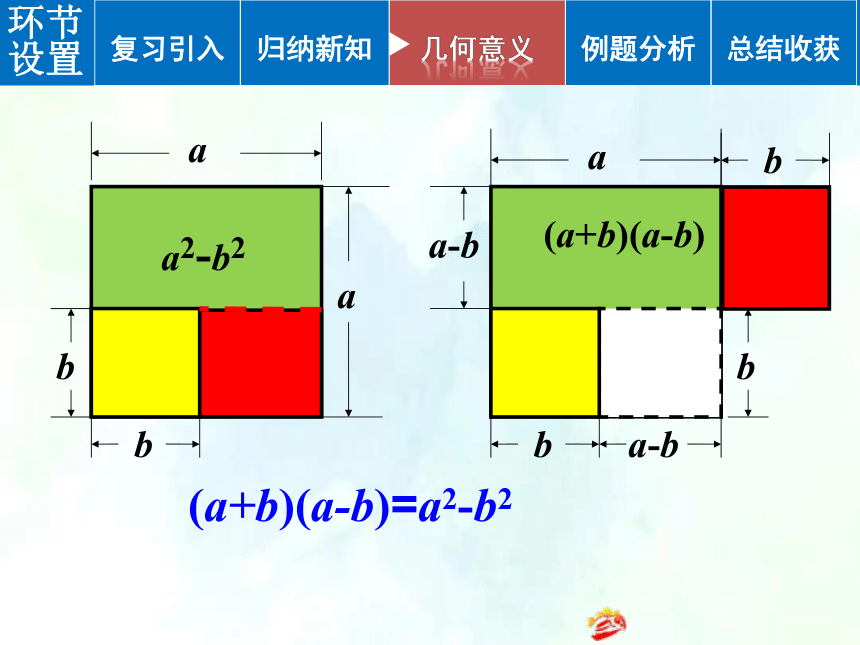
(a+b)(a-b)=a2-b2
a-b
a-b
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
b
a
a
b
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
(a+b)(a-b)=a2-b2
例 计算:
(1)
(2)
(3)102×98
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
辨析
练习2
练习1 下面各式的计算对不对?如果不对,
应当怎样改正?
(1)
(2)
(3)
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
练习3
练习2 计算:
(1)
(2)
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
辨析
练习3
练习3 计算:
(1)
(2)
(3)
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
(1)平方差公式的内容是什么?
(2)应用平方差公式时要注意什么?
(3)本节课体现了哪些数学思想?
例 计算:
(1)
(2)
(3)
(4)102×98
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
辨析
练习2
14.2.1平方差公式
人教版 八年级上册数学
环节设置
复习引入
归纳新知
几何意义
例题分析
计算下列各式:
【问题1】观察这三个运算及运算结果,你能发现等式两边的式子各有什么特点吗?
总结收获
?
平方差公式:
=
【问题2】请你用学过的知识对上述猜想进行验证.
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
【归纳】
两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式:
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
【问题3】你能将这个公式用文字语言进行表述吗?
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
平方差公式:
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
b
a
a
b
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
(a+b)(a-b)=a2-b2
例 计算:
(1)
(2)
(3)102×98
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
辨析
练习2
练习1 下面各式的计算对不对?如果不对,
应当怎样改正?
(1)
(2)
(3)
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
练习3
练习2 计算:
(1)
(2)
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
辨析
练习3
练习3 计算:
(1)
(2)
(3)
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
(1)平方差公式的内容是什么?
(2)应用平方差公式时要注意什么?
(3)本节课体现了哪些数学思想?
例 计算:
(1)
(2)
(3)
(4)102×98
环节设置
复习引入
归纳新知
几何意义
例题分析
总结收获
辨析
练习2
