人教版八年级上册数学14.1.2幂的乘方 优质课件(共24张PPT)
文档属性
| 名称 | 人教版八年级上册数学14.1.2幂的乘方 优质课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 744.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 13:48:55 | ||
图片预览








文档简介
(共24张PPT)
14.1.2幂的乘方
学习目标
1、掌握幂的乘方运算法则。
2、能运用幂的乘方法则进行有关计算。
同底数幂相乘,底数不变,指数相加.
am · an = am+n (m、n都是正整数).
(m是正整数)
(m是正整数)
?
你能用上面的方法,推导出刚才发现的规律吗?
(m是正整数)
(m ,n 都是正整数)
你能用文字语言概括出幂的乘方的运算性质吗?
幂的乘方,底数不变,指数相乘。
幂的乘方,底数不变,指数相乘。
注:字母a可以表示数、单项式和多项式.
(m ,n 都是正整数)
抢答: (1) (2)
(3) (4)
解: (1)
(2)
(3)
(4).
计算
(3)
解: (1) (2)
(3) (4)
(4)
(2)
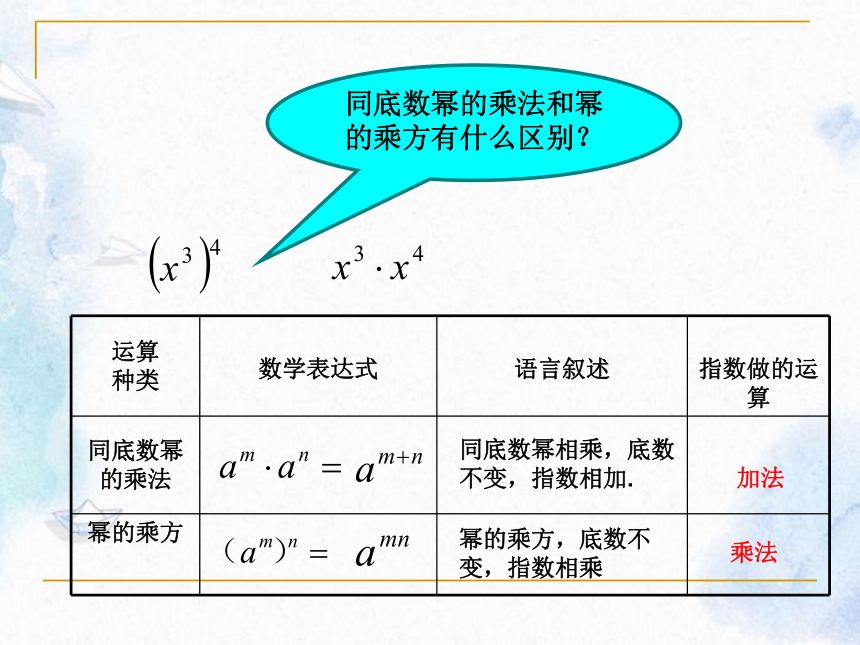
运算
种类
数学表达式
语言叙述
指数做的运算
同底数幂的乘法
幂的乘方
加法
乘法
同底数幂相乘,底数不变,指数相加.
幂的乘方,底数不变,指数相乘
同底数幂的乘法和幂的乘方有什么区别?
计算
(3)
(4)
(2)
多重乘方可以重复运用上述法则:
(m、n、p是正整数)
计算
(1)- ( xm )5
(2)
(3)
下面的计算对不对?若不对,怎样改正?
(1) ( )
(2) ( )
(3) ( )
(4) ( )
×
×
×
×
1、下列运算正确的是( )
A、x6·x3=x18 B、(-x)6· (-x)3=-x9
C、(x3)2=x5 D、 -x6·x3=x9
B
2、下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x · (x5)m (D) x · x5 · xm
C
3、下列运算正确的是( )
A、x2·x3=x6 B、2x2 + 3x2=5x2
C、(x2)3=x8 D、 34 ×34=94
B
如果a2n=5,那么a6n等于多少?
解:a6n =
(a2n )3
=53
=125
计算:
(1)(x2)4
(2) -(y5)2
(3)(a4)2+a2·a6
(4)( m3)3·(m2)3
(5) 已知a3n=8,求an的值.
◆本节课学习了哪些内容?
◆在运用公式时要注意什么?
必做题:课本97页练习,习题14.1第1
⑶⑷题
选做题:已知10a=5,10b=6,求102a+3b
的值
(m、n都是正整数)
法则的推导过程
15.2.2 幂的乘方
运算
种类
数学表达式
语言叙述
指数做的运算
同底数幂的乘法
幂的乘方
加法
乘法
同底数幂相乘,底数不变,指数相加.
幂的乘方,底数不变,指数相乘
填空
(1)
(2)
(3)
如果a2n=5,那么a6n等于多少?
如果还知道am=2,那么a2n+3m等于多少?
下面的计算对不对?若不对,怎样改正?
(1) (a2)3=a5 ( )
(2) a2 a3=a6 ( )
(3) a6+a6=a12 ( )
(4) (xn+1)2= x2n+1 ( )
(5) (a4)3+a3a9=a7+a11= a18 ( )
×
a6
a5
2a6
×
×
×
×
x2n+2
2a12
14.1.2幂的乘方
学习目标
1、掌握幂的乘方运算法则。
2、能运用幂的乘方法则进行有关计算。
同底数幂相乘,底数不变,指数相加.
am · an = am+n (m、n都是正整数).
(m是正整数)
(m是正整数)
?
你能用上面的方法,推导出刚才发现的规律吗?
(m是正整数)
(m ,n 都是正整数)
你能用文字语言概括出幂的乘方的运算性质吗?
幂的乘方,底数不变,指数相乘。
幂的乘方,底数不变,指数相乘。
注:字母a可以表示数、单项式和多项式.
(m ,n 都是正整数)
抢答: (1) (2)
(3) (4)
解: (1)
(2)
(3)
(4).
计算
(3)
解: (1) (2)
(3) (4)
(4)
(2)
运算
种类
数学表达式
语言叙述
指数做的运算
同底数幂的乘法
幂的乘方
加法
乘法
同底数幂相乘,底数不变,指数相加.
幂的乘方,底数不变,指数相乘
同底数幂的乘法和幂的乘方有什么区别?
计算
(3)
(4)
(2)
多重乘方可以重复运用上述法则:
(m、n、p是正整数)
计算
(1)- ( xm )5
(2)
(3)
下面的计算对不对?若不对,怎样改正?
(1) ( )
(2) ( )
(3) ( )
(4) ( )
×
×
×
×
1、下列运算正确的是( )
A、x6·x3=x18 B、(-x)6· (-x)3=-x9
C、(x3)2=x5 D、 -x6·x3=x9
B
2、下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x · (x5)m (D) x · x5 · xm
C
3、下列运算正确的是( )
A、x2·x3=x6 B、2x2 + 3x2=5x2
C、(x2)3=x8 D、 34 ×34=94
B
如果a2n=5,那么a6n等于多少?
解:a6n =
(a2n )3
=53
=125
计算:
(1)(x2)4
(2) -(y5)2
(3)(a4)2+a2·a6
(4)( m3)3·(m2)3
(5) 已知a3n=8,求an的值.
◆本节课学习了哪些内容?
◆在运用公式时要注意什么?
必做题:课本97页练习,习题14.1第1
⑶⑷题
选做题:已知10a=5,10b=6,求102a+3b
的值
(m、n都是正整数)
法则的推导过程
15.2.2 幂的乘方
运算
种类
数学表达式
语言叙述
指数做的运算
同底数幂的乘法
幂的乘方
加法
乘法
同底数幂相乘,底数不变,指数相加.
幂的乘方,底数不变,指数相乘
填空
(1)
(2)
(3)
如果a2n=5,那么a6n等于多少?
如果还知道am=2,那么a2n+3m等于多少?
下面的计算对不对?若不对,怎样改正?
(1) (a2)3=a5 ( )
(2) a2 a3=a6 ( )
(3) a6+a6=a12 ( )
(4) (xn+1)2= x2n+1 ( )
(5) (a4)3+a3a9=a7+a11= a18 ( )
×
a6
a5
2a6
×
×
×
×
x2n+2
2a12
