4.1 正弦和余弦(1) 课件(共24张PPT)
文档属性
| 名称 | 4.1 正弦和余弦(1) 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 19:39:07 | ||
图片预览






文档简介
(共24张PPT)
4.1 正弦和余弦(1)
湘教版九年级上册
教学目标
1. 感知直角三角形的一个锐角的对边与斜边是一个常数;
2. 能准确理解正弦的含义,掌握正弦的概念.
3. 学会求一个锐角的正弦值的方法并能熟练计算.
4. 初步感知锐角三角函数的函数特殊性.
温故知新
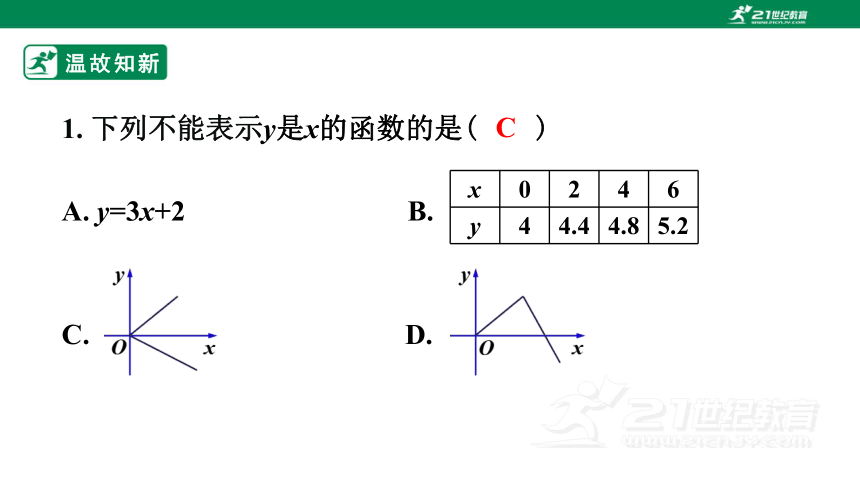
1. 下列不能表示y是x的函数的是( )
A. y=3x+2 B.
C. D.
C
x 0 2 4 6
y 4 4.4 4.8 5.2
温故知新
2. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列说法或结论错误的是( )
A. 由“两角相等的两个三角形相似”得△ADC∽△ACB
B. 图中共有3对相似三角形
C. 由△CDB∽△ACB得
D. 由△ADC∽△CDB得CD =AD·BD
C
温故知新
3. 满足函数概念的条件有哪些?
①有两个变量 ,且其中一个变量随着另一个量而变化;
②对于自变量取的每一个值,因变量都有唯一的值和它对应.
①平行于三角形一边的直线截得的三角形与原三角形相似;
②两角分别相等的两个三角形相似(判定定理1);
③两边成比例且夹角相等的两个三角形相似(判定定理2);
④三边成比例的两个三角形相似(判定定理3).
4. 判定三角形相似的方法有哪些?
新知讲解
画一个直角三角形,其中一个锐角为65°,量出65°角的对边长度和斜边长度,计算:
做一做
与同桌和邻近桌的同学交流,计算出的比值是否相等(精确到0.01)?
= = .
65°角的对边
斜边
新知讲解
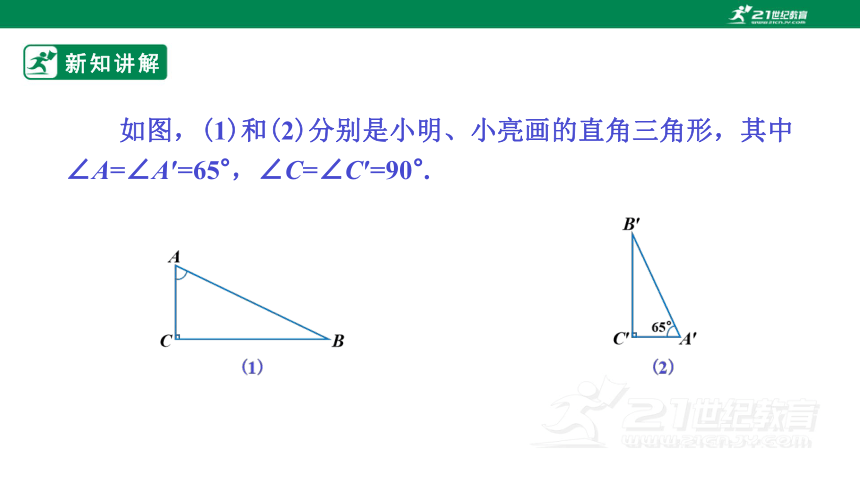
如图,(1)和(2)分别是小明、小亮画的直角三角形,其中∠A=∠A′=65°,∠C=∠C′=90°.
新知讲解
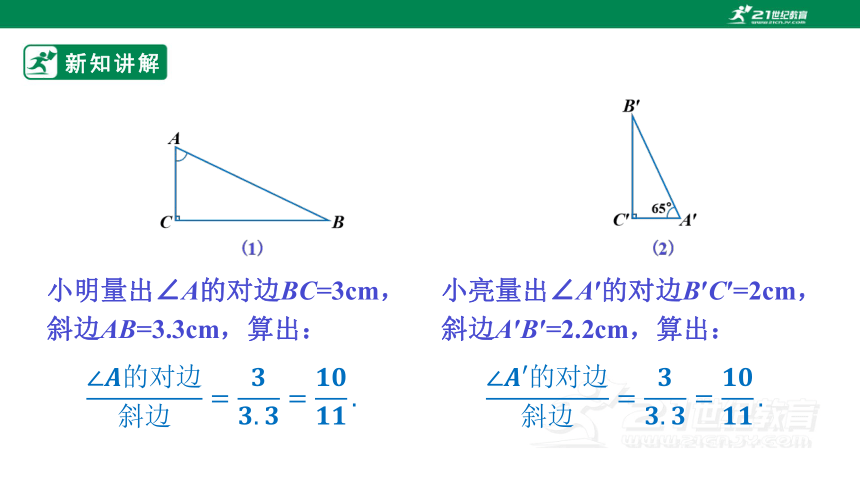
小明量出∠A的对边BC=3cm,斜边AB=3.3cm,算出:
小亮量出∠A′的对边B′C′=2cm,斜边A′B′=2.2cm,算出:
新知讲解
由此猜测:在有一个锐角为65°的直角三角形中, 65°角的对边与斜边的比值是一个常数,它等于.
这个猜测是真的吗?若把65°换成任意一个锐角α,则这个角的对边与斜边的比值是否也是一个常数呢?
新知讲解
如图4-2,△ABC和△DEF都是直角三角形,其中∠A=∠D=α,∠C=∠F=90°,则成立吗?为什么?
探究
新知讲解
∵ ∠A=∠D=α,∠C=∠F=90°,
∴ Rt△ABC∽Rt△DEF.
∴
即 BC·DE=AB·EF.
∴
新知讲解
这说明,在有一个锐角等于α的所有直角三角形中,角α的对边与斜边的比值是一个常数,与直角三角形的大小无关.
你能说说上面的探究结论说明了什么吗?
新知讲解
如图4-3,在直角三角形中,我们把锐角α的对边与斜边的比叫作角α的正弦,记作sinα,即
定义
sinα=
角α的对边
斜边
新知讲解
根据“在直角三角形中,30°角所对的直角边等于斜边的一半”,容易得到
例题教学
例1 如图4-4,在Rt△ABC中,∠C=90°,BC=3,AB=5.
(1)求sinA的值;
(2)求sinB的值.
分析 (1)求sinA的值就是求∠A的对边BC与斜边AB的比;(2)求sinB的值要先利用勾股定理求出∠B的对边AC.
例题教学
(2)∠B的对边AC,根据勾股定理,得
AC =AB -BC =5 -3 =16.
解 (1)∠A的对边BC=3,斜边AB=5. 于是
于是 AC=4.
因此
课堂总结
1、在有一个锐角等于α的所有直角三角形中,角α的对边与
斜边的比值是一个 ,与直角三角形的大小 .
2、在直角三角形中,我们把锐角α的对边与斜边的比叫作
角α的 ,记作 .即
常数
sinα
无关
正弦
3、sin30°= .
温故知新
1. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中不正确的是( )
A. sinB= B. sinB=
C. sinB= D. sinB=
C
课堂练习
2. (云南中考)在△ABC中,∠ABC=90°.若AC=100,
sinA=, 则AB的长是( )
A. B. C. 60 D. 80
D
板书设计
4.1 正弦和余弦(1)
正弦的概念
正弦的表示方法
求直角三角形中的锐角的正弦
作业布置
第111页课后练习第1、2题
1. 在直角三角形ABC中,∠C=90°,AB=13,BC=5.求sinA, sinB的值.
作业布置
2. 如图,在平面直角坐标系内有一点P(3,4),连接OP,求OP与x轴正方向所夹锐角α的正弦值.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.1 正弦和余弦(1)
湘教版九年级上册
教学目标
1. 感知直角三角形的一个锐角的对边与斜边是一个常数;
2. 能准确理解正弦的含义,掌握正弦的概念.
3. 学会求一个锐角的正弦值的方法并能熟练计算.
4. 初步感知锐角三角函数的函数特殊性.
温故知新
1. 下列不能表示y是x的函数的是( )
A. y=3x+2 B.
C. D.
C
x 0 2 4 6
y 4 4.4 4.8 5.2
温故知新
2. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列说法或结论错误的是( )
A. 由“两角相等的两个三角形相似”得△ADC∽△ACB
B. 图中共有3对相似三角形
C. 由△CDB∽△ACB得
D. 由△ADC∽△CDB得CD =AD·BD
C
温故知新
3. 满足函数概念的条件有哪些?
①有两个变量 ,且其中一个变量随着另一个量而变化;
②对于自变量取的每一个值,因变量都有唯一的值和它对应.
①平行于三角形一边的直线截得的三角形与原三角形相似;
②两角分别相等的两个三角形相似(判定定理1);
③两边成比例且夹角相等的两个三角形相似(判定定理2);
④三边成比例的两个三角形相似(判定定理3).
4. 判定三角形相似的方法有哪些?
新知讲解
画一个直角三角形,其中一个锐角为65°,量出65°角的对边长度和斜边长度,计算:
做一做
与同桌和邻近桌的同学交流,计算出的比值是否相等(精确到0.01)?
= = .
65°角的对边
斜边
新知讲解
如图,(1)和(2)分别是小明、小亮画的直角三角形,其中∠A=∠A′=65°,∠C=∠C′=90°.
新知讲解
小明量出∠A的对边BC=3cm,斜边AB=3.3cm,算出:
小亮量出∠A′的对边B′C′=2cm,斜边A′B′=2.2cm,算出:
新知讲解
由此猜测:在有一个锐角为65°的直角三角形中, 65°角的对边与斜边的比值是一个常数,它等于.
这个猜测是真的吗?若把65°换成任意一个锐角α,则这个角的对边与斜边的比值是否也是一个常数呢?
新知讲解
如图4-2,△ABC和△DEF都是直角三角形,其中∠A=∠D=α,∠C=∠F=90°,则成立吗?为什么?
探究
新知讲解
∵ ∠A=∠D=α,∠C=∠F=90°,
∴ Rt△ABC∽Rt△DEF.
∴
即 BC·DE=AB·EF.
∴
新知讲解
这说明,在有一个锐角等于α的所有直角三角形中,角α的对边与斜边的比值是一个常数,与直角三角形的大小无关.
你能说说上面的探究结论说明了什么吗?
新知讲解
如图4-3,在直角三角形中,我们把锐角α的对边与斜边的比叫作角α的正弦,记作sinα,即
定义
sinα=
角α的对边
斜边
新知讲解
根据“在直角三角形中,30°角所对的直角边等于斜边的一半”,容易得到
例题教学
例1 如图4-4,在Rt△ABC中,∠C=90°,BC=3,AB=5.
(1)求sinA的值;
(2)求sinB的值.
分析 (1)求sinA的值就是求∠A的对边BC与斜边AB的比;(2)求sinB的值要先利用勾股定理求出∠B的对边AC.
例题教学
(2)∠B的对边AC,根据勾股定理,得
AC =AB -BC =5 -3 =16.
解 (1)∠A的对边BC=3,斜边AB=5. 于是
于是 AC=4.
因此
课堂总结
1、在有一个锐角等于α的所有直角三角形中,角α的对边与
斜边的比值是一个 ,与直角三角形的大小 .
2、在直角三角形中,我们把锐角α的对边与斜边的比叫作
角α的 ,记作 .即
常数
sinα
无关
正弦
3、sin30°= .
温故知新
1. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中不正确的是( )
A. sinB= B. sinB=
C. sinB= D. sinB=
C
课堂练习
2. (云南中考)在△ABC中,∠ABC=90°.若AC=100,
sinA=, 则AB的长是( )
A. B. C. 60 D. 80
D
板书设计
4.1 正弦和余弦(1)
正弦的概念
正弦的表示方法
求直角三角形中的锐角的正弦
作业布置
第111页课后练习第1、2题
1. 在直角三角形ABC中,∠C=90°,AB=13,BC=5.求sinA, sinB的值.
作业布置
2. 如图,在平面直角坐标系内有一点P(3,4),连接OP,求OP与x轴正方向所夹锐角α的正弦值.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
