4.1 正弦和余弦(3) 课件(共26张PPT)
文档属性
| 名称 | 4.1 正弦和余弦(3) 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 19:36:42 | ||
图片预览





文档简介
(共26张PPT)
4.1 正弦和余弦(3)
湘教版九年级上册
教学目标
1. 理解直角三角形的一个锐角的邻边与斜边是一个常数;
2. 能准确理解余弦的函数含义,掌握正弦的概念.
3. 学会求一个锐角的余弦值的方法并能熟练计算.
4. 能灵活运用正弦或余弦解决求直角三角形的边的问题.
温故知新
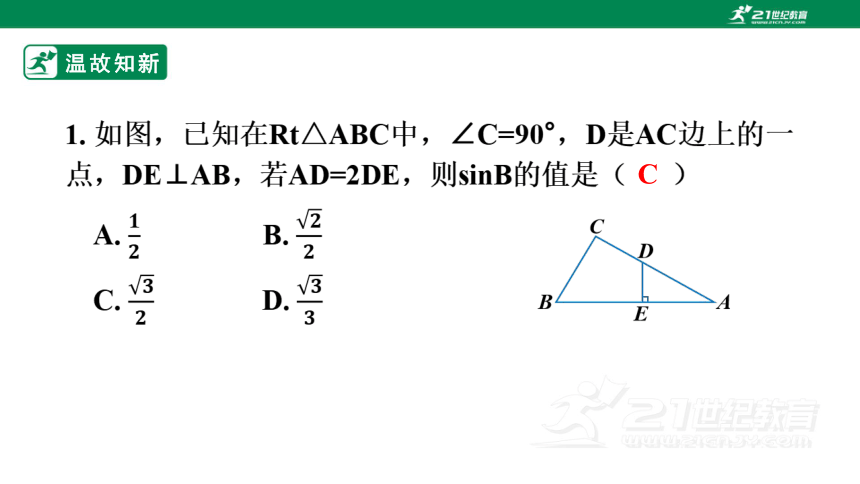
1. 如图,已知在Rt△ABC中,∠C=90°,D是AC边上的一点,DE⊥AB,若AD=2DE,则sinB的值是( )
A. B.
C. D.
C
温故知新
2. 如图,在平面直角坐标系中,点A的坐标是(5,4),则sinα的值是( )
A. B.
C. D.
D
新知讲解
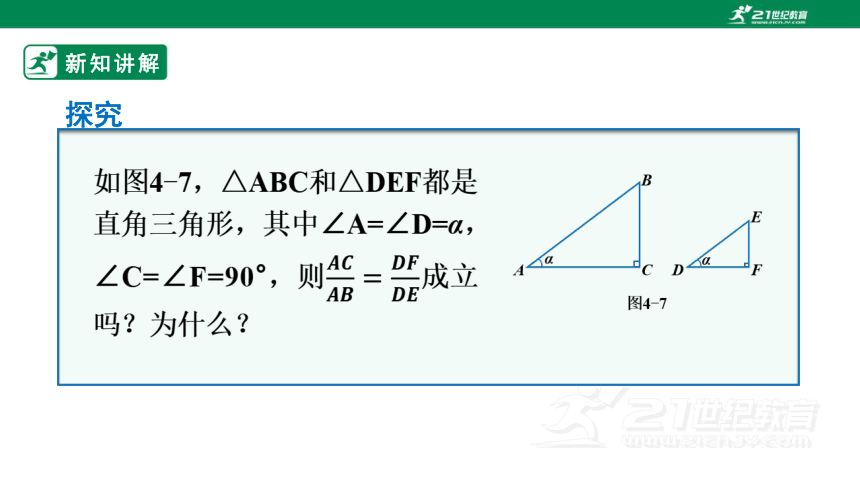
如图4-7,△ABC和△DEF都是直角三角形,其中∠A=∠D=α,∠C=∠F=90°,则成立吗?为什么?
探究
新知讲解
∵ ∠A=∠D=α,∠C=∠F=90°,
∴ ∠B=∠F.
∴ sinB=sinE.
∴
新知讲解
这说明,在有一个锐角等于α的所有直角三角形中,角α的邻与斜边的比值是一个常数,与直角三角形的大小无关.
新知讲解
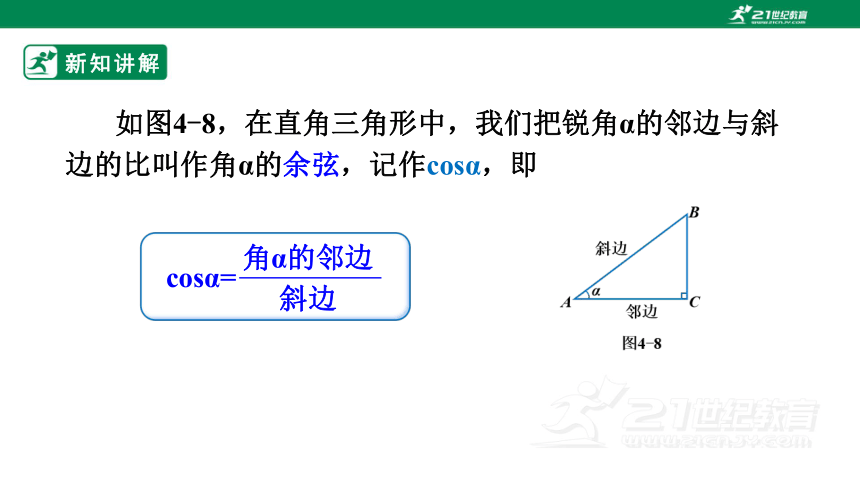
如图4-8,在直角三角形中,我们把锐角α的邻边与斜边的比叫作角α的余弦,记作cosα,即
cosα=
角α的邻边
斜边
新知讲解
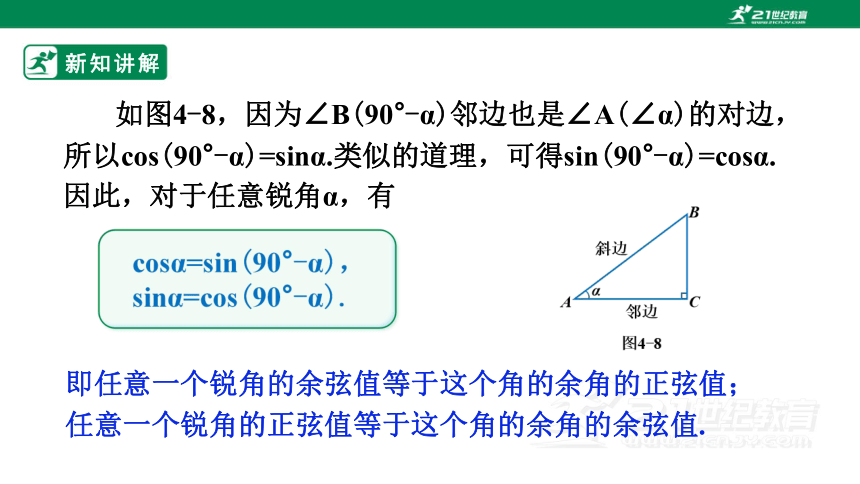
如图4-8,因为∠B(90°-α)邻边也是∠A(∠α)的对边,所以cos(90°-α)=sinα.类似的道理,可得sin(90°-α)=cosα. 因此,对于任意锐角α,有
cosα=sin(90°-α),
sinα=cos(90°-α).
即任意一个锐角的余弦值等于这个角的余角的正弦值;
任意一个锐角的正弦值等于这个角的余角的余弦值.
例题教学
例3 求cos30°,cos45°,cos60°的值.
思路 因为一个锐角的余弦值等于这个角的余角的正弦值,所以可以把题中各角的余弦分别转化为它们的余角即60°,45°,30°的正弦来计算.
解:cos30°=
sin(90-30°)=sin60°=,
cos45°=
sin(90-45°)=sin45°=,
cos60°=
sin(90-60°)=sin30°=.
新知讲解
对于一般锐角α(30°,45°,60°除外)的余弦值,我们可用计算器来求.
例如求50°角的余弦值,可以在计算器上依次按键
,显示结果为0.6427….
cos
5
0
新知讲解
如果已知余弦值,我们也可以利用计算器求出它的对应锐角.
例如,已知cosα=0.8661,依次按键
,显示结果为29.9914…,表示角α约等于30°.
6
6
.
2ndF
cos
0
8
1
新知讲解
利用计算器计算:
(1)cos15°≈ (精确到0.0001);
(2)cos50°48′≈ (精确到0.0001);
(3)若cosα=0.9659,则α≈ (精确到0.1°);
(4)若cosα=0.2588,则α≈ (精确到0.1°).
做一做
0.6428
0.2672
31.5°
54.0°
例题教学
例4 计算:cos30°-cos60°+cos 45°.
cos30°-cos60°+cos 45°
解:
课堂练习
1. 如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,则cosB的值为( )
A. B.
C. D.
C
课堂练习
2. 若α是锐角,cosα=,则sin(90°-α)的值是( )
A. B. C. D.
A
课堂总结
1. 什么叫作余弦?记作什么?
在直角三角形中,锐角α的邻边与斜边的比叫作角α的余弦,记作cosα.
2. 互为余角的两个锐角的正弦和余弦有什么关系?
任意一个锐角的余弦值等于这个角的余角的正弦值;
任意一个锐角的正弦值等于这个角的余角的余弦值.
即
cosα=sin(90°-α),sinα=cos(90°-α).
课堂总结
3. 特殊角30°,45°,60°的正弦值、余弦值分别是多少?
4. 用计算器如何计算余弦值?已知锐角α的余弦,怎样求α?
板书设计
4.1 正弦和余弦(3)
余弦的概念
互为余角的角的正弦和余弦关系
30°,45°,60°角的余弦值
用计算器求余弦或根据余弦求角
作业布置
第115页课后练习第1、2、3、4题
1. 如图,在Rt△ABC中,∠C=90°,AC=5,AB=7,求cosA,cosB的值.
提示:求时,要先根据勾股定理求出BC,然后根据余弦的概念找出邻边和斜边,进行计算.
作业布置
2. 用计算器求下列锐角的余弦值(精确到0.0001).
(1)35°; (2)68°12′; (3)9°42′.
答案:(1)cos35°≈0.8192;
(2)cos68°12′≈0.3714;
(3)cos9°42′≈0.9857.
作业布置
3. 已知下列余弦值,用计算器求对应的锐角α(精确到0.1°).
(1)cosα=0.1087; (2)cosα=0.7081.
答案:(1)α≈83.8°; (2)α≈44.9°.
作业布置
4. 计算:
(1)cos 60°-sin 45°; (2)1-2cos30°cos45°.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
作业布置
4. 计算:
(1)cos 60°-sin 45°; (2)1-2cos30°cos45°.
解:(1)cos 60°-sin 45°=;
(2)1-2cos30°cos45°=.
4.1 正弦和余弦(3)
湘教版九年级上册
教学目标
1. 理解直角三角形的一个锐角的邻边与斜边是一个常数;
2. 能准确理解余弦的函数含义,掌握正弦的概念.
3. 学会求一个锐角的余弦值的方法并能熟练计算.
4. 能灵活运用正弦或余弦解决求直角三角形的边的问题.
温故知新
1. 如图,已知在Rt△ABC中,∠C=90°,D是AC边上的一点,DE⊥AB,若AD=2DE,则sinB的值是( )
A. B.
C. D.
C
温故知新
2. 如图,在平面直角坐标系中,点A的坐标是(5,4),则sinα的值是( )
A. B.
C. D.
D
新知讲解
如图4-7,△ABC和△DEF都是直角三角形,其中∠A=∠D=α,∠C=∠F=90°,则成立吗?为什么?
探究
新知讲解
∵ ∠A=∠D=α,∠C=∠F=90°,
∴ ∠B=∠F.
∴ sinB=sinE.
∴
新知讲解
这说明,在有一个锐角等于α的所有直角三角形中,角α的邻与斜边的比值是一个常数,与直角三角形的大小无关.
新知讲解
如图4-8,在直角三角形中,我们把锐角α的邻边与斜边的比叫作角α的余弦,记作cosα,即
cosα=
角α的邻边
斜边
新知讲解
如图4-8,因为∠B(90°-α)邻边也是∠A(∠α)的对边,所以cos(90°-α)=sinα.类似的道理,可得sin(90°-α)=cosα. 因此,对于任意锐角α,有
cosα=sin(90°-α),
sinα=cos(90°-α).
即任意一个锐角的余弦值等于这个角的余角的正弦值;
任意一个锐角的正弦值等于这个角的余角的余弦值.
例题教学
例3 求cos30°,cos45°,cos60°的值.
思路 因为一个锐角的余弦值等于这个角的余角的正弦值,所以可以把题中各角的余弦分别转化为它们的余角即60°,45°,30°的正弦来计算.
解:cos30°=
sin(90-30°)=sin60°=,
cos45°=
sin(90-45°)=sin45°=,
cos60°=
sin(90-60°)=sin30°=.
新知讲解
对于一般锐角α(30°,45°,60°除外)的余弦值,我们可用计算器来求.
例如求50°角的余弦值,可以在计算器上依次按键
,显示结果为0.6427….
cos
5
0
新知讲解
如果已知余弦值,我们也可以利用计算器求出它的对应锐角.
例如,已知cosα=0.8661,依次按键
,显示结果为29.9914…,表示角α约等于30°.
6
6
.
2ndF
cos
0
8
1
新知讲解
利用计算器计算:
(1)cos15°≈ (精确到0.0001);
(2)cos50°48′≈ (精确到0.0001);
(3)若cosα=0.9659,则α≈ (精确到0.1°);
(4)若cosα=0.2588,则α≈ (精确到0.1°).
做一做
0.6428
0.2672
31.5°
54.0°
例题教学
例4 计算:cos30°-cos60°+cos 45°.
cos30°-cos60°+cos 45°
解:
课堂练习
1. 如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,则cosB的值为( )
A. B.
C. D.
C
课堂练习
2. 若α是锐角,cosα=,则sin(90°-α)的值是( )
A. B. C. D.
A
课堂总结
1. 什么叫作余弦?记作什么?
在直角三角形中,锐角α的邻边与斜边的比叫作角α的余弦,记作cosα.
2. 互为余角的两个锐角的正弦和余弦有什么关系?
任意一个锐角的余弦值等于这个角的余角的正弦值;
任意一个锐角的正弦值等于这个角的余角的余弦值.
即
cosα=sin(90°-α),sinα=cos(90°-α).
课堂总结
3. 特殊角30°,45°,60°的正弦值、余弦值分别是多少?
4. 用计算器如何计算余弦值?已知锐角α的余弦,怎样求α?
板书设计
4.1 正弦和余弦(3)
余弦的概念
互为余角的角的正弦和余弦关系
30°,45°,60°角的余弦值
用计算器求余弦或根据余弦求角
作业布置
第115页课后练习第1、2、3、4题
1. 如图,在Rt△ABC中,∠C=90°,AC=5,AB=7,求cosA,cosB的值.
提示:求时,要先根据勾股定理求出BC,然后根据余弦的概念找出邻边和斜边,进行计算.
作业布置
2. 用计算器求下列锐角的余弦值(精确到0.0001).
(1)35°; (2)68°12′; (3)9°42′.
答案:(1)cos35°≈0.8192;
(2)cos68°12′≈0.3714;
(3)cos9°42′≈0.9857.
作业布置
3. 已知下列余弦值,用计算器求对应的锐角α(精确到0.1°).
(1)cosα=0.1087; (2)cosα=0.7081.
答案:(1)α≈83.8°; (2)α≈44.9°.
作业布置
4. 计算:
(1)cos 60°-sin 45°; (2)1-2cos30°cos45°.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
作业布置
4. 计算:
(1)cos 60°-sin 45°; (2)1-2cos30°cos45°.
解:(1)cos 60°-sin 45°=;
(2)1-2cos30°cos45°=.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
