人教B版(2019)数学必修第二册期中复习:函数的图象达标训练(含答案)
文档属性
| 名称 | 人教B版(2019)数学必修第二册期中复习:函数的图象达标训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 352.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 16:43:55 | ||
图片预览



文档简介
函数的图象
一、单项选择题
1.函数y=-ex的图象( )
A.与y=ex的图象关于y轴对称
B.与y=ex的图象关于坐标原点对称
C.与y=e-x的图象关于y轴对称
D.与y=e-x的图象关于坐标原点对称
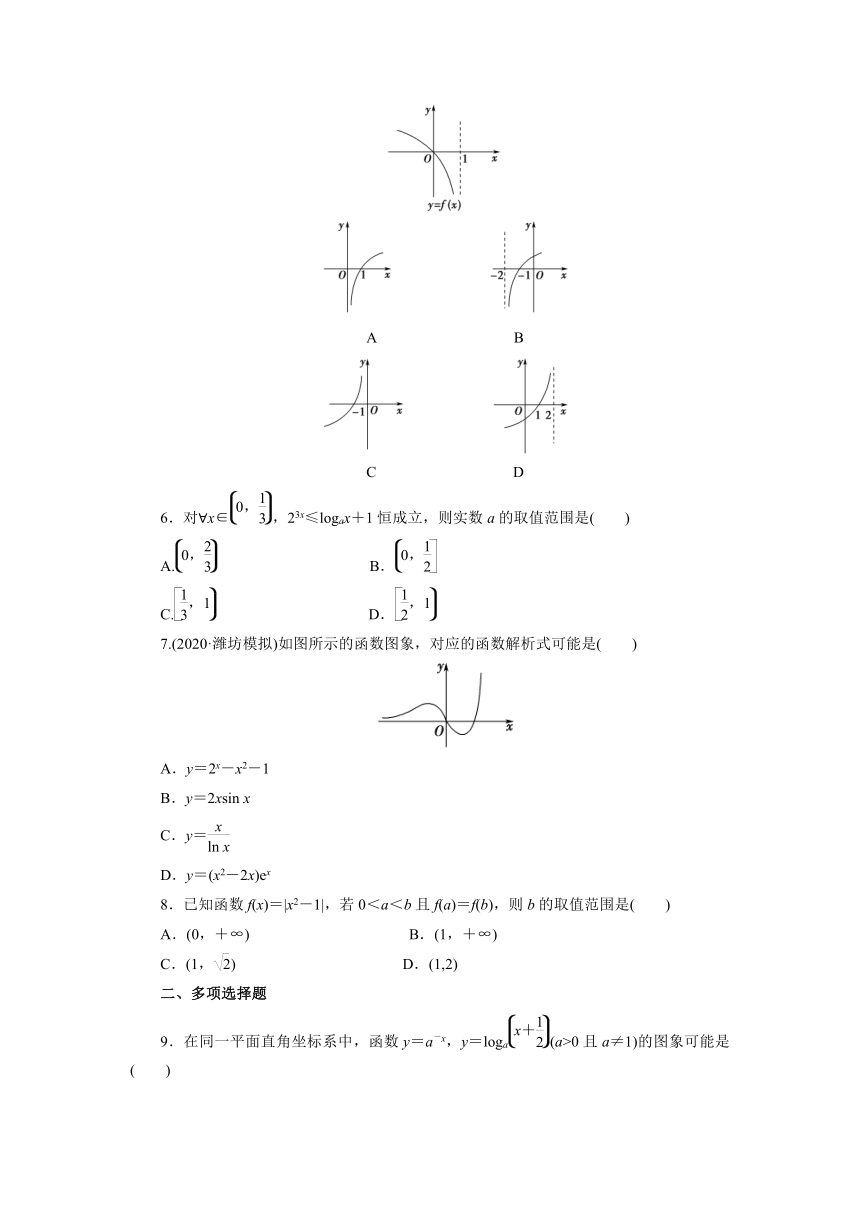
2.函数y=lg|x-1|的图象是( )
A B
C D
3.函数f(x)=的图象大致为( )
A B
C D
4.下列函数中,其图象与函数y=log2x的图象关于直线y=1对称的是( )
A.y=log2 B.y=log2
C.y=log2(2x) D.y=log2(4x)
5.若函数y=f(x)的图象如图所示,则函数y=-f(x+1)的图象大致为( )
A B
C D
6.对 x∈,23x≤logax+1恒成立,则实数a的取值范围是( )
A. B.
C. D.
7.(2020·潍坊模拟)如图所示的函数图象,对应的函数解析式可能是( )
A.y=2x-x2-1
B.y=2xsin x
C.y=
D.y=(x2-2x)ex
8.已知函数f(x)=|x2-1|,若0<a<b且f(a)=f(b),则b的取值范围是( )
A.(0,+∞) B.(1,+∞)
C.(1,) D.(1,2)
二、多项选择题
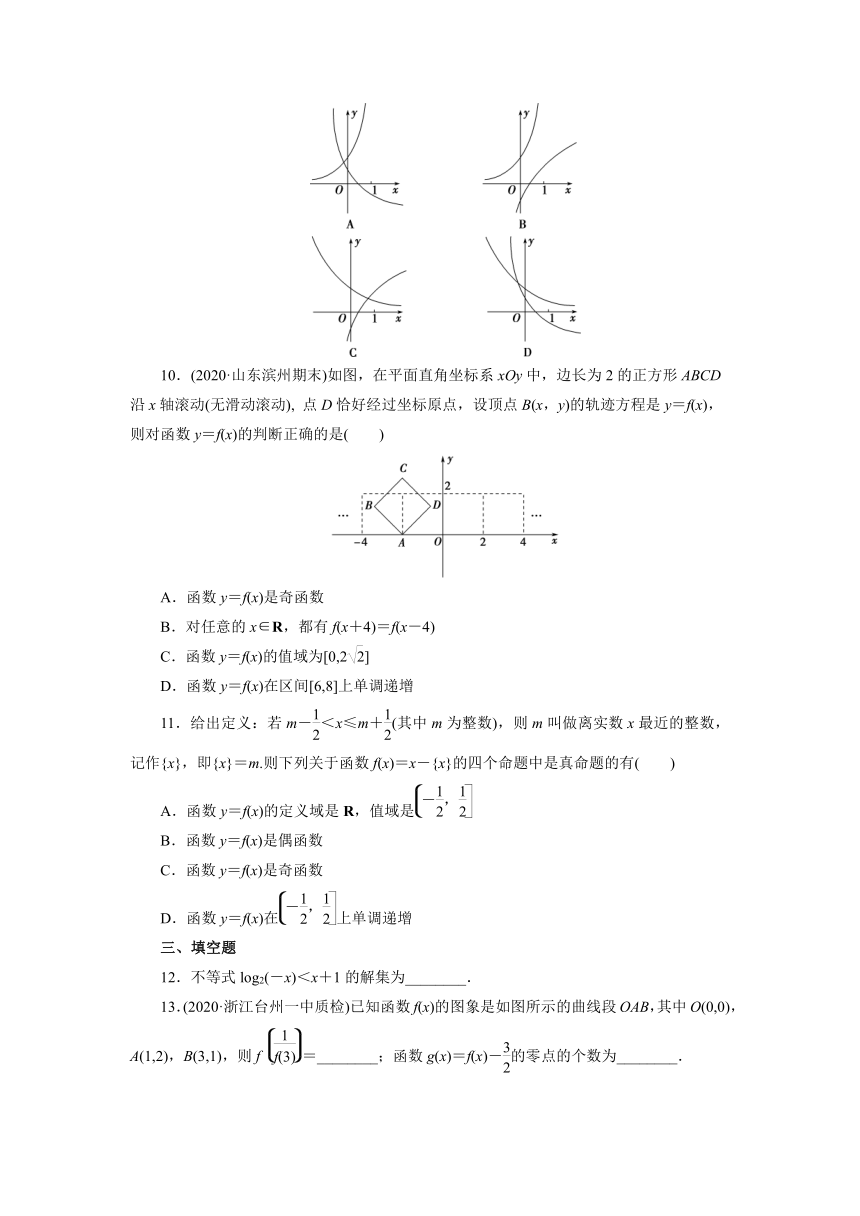
9.在同一平面直角坐标系中,函数y=a-x,y=loga(a>0且a≠1)的图象可能是( )
10.(2020·山东滨州期末)如图,在平面直角坐标系xOy中,边长为2的正方形ABCD沿x轴滚动(无滑动滚动), 点D恰好经过坐标原点,设顶点B(x,y)的轨迹方程是y=f(x),则对函数y=f(x)的判断正确的是( )
A.函数y=f(x)是奇函数
B.对任意的x∈R,都有f(x+4)=f(x-4)
C.函数y=f(x)的值域为[0,2]
D.函数y=f(x)在区间[6,8]上单调递增
11.给出定义:若m-<x≤m+(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.则下列关于函数f(x)=x-{x}的四个命题中是真命题的有( )
A.函数y=f(x)的定义域是R,值域是
B.函数y=f(x)是偶函数
C.函数y=f(x)是奇函数
D.函数y=f(x)在上单调递增
三、填空题
12.不等式log2(-x)<x+1的解集为________.
13.(2020·浙江台州一中质检)已知函数f(x)的图象是如图所示的曲线段OAB,其中O(0,0),A(1,2),B(3,1),则f =________;函数g(x)=f(x)-的零点的个数为________.
14.设函数f(x)=|x+a|,g(x)=x-1,对于任意的x∈R,不等式f(x)≥g(x)恒成立,则实数a的取值范围是________.
15.已知函数f(x)=若|f(x)|≥ax,则a的取值范围是________.
四、解答题
16.画出下列函数的图象.
(1)y=eln x;
(2)y=;
(3)y=|x2-2x-1|.
17.作出函数y=log2|x+1|的图象,由图象指出函数的单调区间,并说明它的图象可由函数y=log2x的图象经过怎样的变换而得到.
18.已知函数f(x)=
(1)在如图所示给定的直角坐标系内画出f(x)的图象;
(2)写出f(x)的单调递增区间;
(3)由图象指出当x取什么值时f(x)有最值.
19.已知函数f(x)=x|m-x|(x∈R),且f(4)=0.
(1)求实数m的值;
(2)作出函数f(x)的图象;
(3)若方程f(x)=a只有一个实数根,求a的取值范围.
20.已知函数f(x)=2x,x∈R.
(1)当m取何值时,方程|f(x)-2|=m有一个解?两个解?
(2)若不等式[f(x)]2+f(x)-m>0在R上恒成立,求m的取值范围.
参考答案
1.D
解析:由点(x,y)关于原点的对称点是(-x,-y),可知D正确.
2.A
解析:函数y=lg|x-1|的定义域为(-∞,1)∪(1,+∞),则排除B,D,当x=0时,y=0,排除C,故选A.
3.C
解析:因为y=x2-1与y=e|x|都是偶函数,所以f(x)=为偶函数,排除A,B,又由x→+∞时,f(x)→0,x→-∞时,f(x)→0,排除D,故选C.
4.B
解析:设P(x,y)为所求函数图象上的任意一点,它关于直线y=1对称的点是Q(x,2-y),由题意知点Q(x,2-y)在函数y=log2x的图象上,则2-y=log2x,即y=2-log2x=log2,故选B.
5.C
解析:要想由y=f(x)的图象得到y=-f(x+1)的图象,需要先将y=f(x)的图象关于x轴对称得到y=-f(x)的图象,然后向左平移一个单位长度得到y=-f(x+1)的图象,根据上述步骤可知C正确.故选C.
6.C
解析:若23x≤logax+1在上恒成立,则0<a<1,利用数形结合思想画出指数函数与对数函数图象(图略),易得loga+1≥,解得≤a<1,故选C.
7.D
解析:由函数图象知,函数的定义域为R,既不是奇函数也不是偶函数,则排除B、C,由图象知,当x=-2时,y>0,则排除A,故选D.
8. C
解析:作出函数f(x)=|x2-1|在区间(0,+∞)上的图象如图所示,
作出直线y=1,交f(x)的图象于点B,由x2-1=1可得xB=,
结合函数图象可得b的取值范围是(1,).
9.AC
解析:函数y=a-x与y=loga(a>0且a≠1)的单调性相反,所以排除B,D项;
当a>1时,可能的图象是C项;
当0故选AC.
10.BCD
解析:由题意得,
当-4≤x<-2时,顶点B(x,y)的轨迹是以点A(-2,0)为圆心,2为半径的圆;
当-2≤x<2时,顶点B(x,y)的轨迹是以点(0,0)为圆心,2为半径的圆;
当2≤x<4时,顶点B(x,y)的轨迹是以点(2,0)为圆心,2为半径的圆;
当4≤x<6时,顶点B(x,y)的轨迹是以点(4,0)为圆心,2为半径的圆,与当-4≤x<-2时,B(x,y)的轨迹的形状相同.
因此函数y=f(x)在[-4,4]上的图象恰好为函数y=f(x)的一个周期的图象,所以函数y=f(x)的周期是8,作出y=f(x)在[-4,4]上的图象如图所示:
由图象及题意得,该函数为偶函数,故A错误;
因为函数y=f(x)的周期为8,所以f(x+8)=f(x),所以f(x+4)=f(x-4),故B正确;
由图象可得,该函数的值域为[0,2],故C正确;
因为该函数是以8为周期的函数,所以函数y=f(x)在区间[6,8]上的图象与在区间[-2,0]上的图象相同,所以y=f(x)在[6,8]上单调递增,故D正确.
故选BCD.
11.AD
解析:化简函数解析式可得,
f(x)=x-{x}=
画出该函数的图象,如图所示,
由图象可知A,D正确.
12.答案:(-1,0)
解析:在同一坐标系中画出函数y=log2(-x)和y=x+1的图象如图所示:
由图象知,不等式log2(-x)<x+1的解集为(-1,0).
13.答案:2 2
解析:由图可知,f(3)=1,故f =f(1)=2.
函数g(x)=f(x)-的零点的个数为函数y=f(x)与函数y=的图象的交点个数,
由图象可知,有2个交点,故零点的个数为2.
14.答案: [-1,+∞)
解析:如图,作出函数f(x)=|x+a|与g(x)=x-1的图象,
观察图象可知:当且仅当-a≤1,即a≥-1时,不等式f(x)≥g(x)恒成立,因此a的取值范围是[-1,+∞).
15.解析: [-2,0]
解析:可画出|f(x)|的图象如图所示.
当a=0时,|f(x)|≥ax=0恒成立,
所以a=0满足题意;
当a>0时,在x<0时,|f(x)|≥ax恒成立,所以只需x>0时,ln(x+1)≥ax成立.
对比对数函数与正比例函数的增长速度发现,一定存在ln(x+1)0不满足条件;
当a<0时,在x>0时满足题意;
当x≤0时,只需x2-2x≥ax成立,
即直线在抛物线下方,即a≥x-2恒成立,则a≥-2.
综上,a的取值范围为[-2,0].
16.解: (1)因为函数的定义域为{x|x>0}且y=eln x=x(x>0),所以其图象如图①所示.
图① 图②
(2)y==1+,先作出y=的图象,将其图象向右平移1个单位,再向上平移1个单位,即得y=的图象,如图②.
(3)先作出函数y=x2-2x-1的图象,然后x轴上方的图象不变,把x轴下方的图象以x轴为对称轴,翻折到x轴上方,得到y=|x2-2x-1|的图象,如图③中实线部分.
图③
17.解:作出函数y=log2x的图象,将其关于y轴对称得到函数y=log2|x|的图象,再将图象向左平移1个单位长度就得到函数y=log2|x+1|的图象(如图所示).由图知,函数y=log2|x+1|的单调递减区间为(-∞,-1),单调递增区间为(-1,+∞).
18.解:(1)函数f(x)的图象如图所示.
(2)由图象可知,函数f(x)的单调递增区间为[-1,0],[2,5].
(3)由图象知当x=2时,f(x)min=f(2)=-1,
当x=0时,f(x)max=f(0)=3.
19.解:(1)因为f(4)=0,所以4|m-4|=0,即m=4.
(2)f(x)=x|x-4|=
f(x)的图象如图所示.
(3)由f(x)的图象可知,当a>4或a<0时,f(x)的图象与直线y=a只有一个交点,即方程f(x)=a只有一个实数根,即a的取值范围是(-∞,0)∪(4,+∞).
20.解:(1)令F(x)=|f(x)-2|=|2x-2|,G(x)=m,画出F(x)的图象如图所示,
由图象看出,当m=0或m≥2时,函数F(x)与G(x)的图象只有一个交点,原方程有一个解;
当0(2)令f(x)=t(t>0),H(t)=t2+t,
因为H(t)=-在区间(0,+∞)上是增函数,
所以H(t)>H(0)=0.
因此要使t2+t>m在区间(0,+∞)上恒成立,
应有m≤0,
即m的取值范围为(-∞,0].
一、单项选择题
1.函数y=-ex的图象( )
A.与y=ex的图象关于y轴对称
B.与y=ex的图象关于坐标原点对称
C.与y=e-x的图象关于y轴对称
D.与y=e-x的图象关于坐标原点对称
2.函数y=lg|x-1|的图象是( )
A B
C D
3.函数f(x)=的图象大致为( )
A B
C D
4.下列函数中,其图象与函数y=log2x的图象关于直线y=1对称的是( )
A.y=log2 B.y=log2
C.y=log2(2x) D.y=log2(4x)
5.若函数y=f(x)的图象如图所示,则函数y=-f(x+1)的图象大致为( )
A B
C D
6.对 x∈,23x≤logax+1恒成立,则实数a的取值范围是( )
A. B.
C. D.
7.(2020·潍坊模拟)如图所示的函数图象,对应的函数解析式可能是( )
A.y=2x-x2-1
B.y=2xsin x
C.y=
D.y=(x2-2x)ex
8.已知函数f(x)=|x2-1|,若0<a<b且f(a)=f(b),则b的取值范围是( )
A.(0,+∞) B.(1,+∞)
C.(1,) D.(1,2)
二、多项选择题
9.在同一平面直角坐标系中,函数y=a-x,y=loga(a>0且a≠1)的图象可能是( )
10.(2020·山东滨州期末)如图,在平面直角坐标系xOy中,边长为2的正方形ABCD沿x轴滚动(无滑动滚动), 点D恰好经过坐标原点,设顶点B(x,y)的轨迹方程是y=f(x),则对函数y=f(x)的判断正确的是( )
A.函数y=f(x)是奇函数
B.对任意的x∈R,都有f(x+4)=f(x-4)
C.函数y=f(x)的值域为[0,2]
D.函数y=f(x)在区间[6,8]上单调递增
11.给出定义:若m-<x≤m+(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.则下列关于函数f(x)=x-{x}的四个命题中是真命题的有( )
A.函数y=f(x)的定义域是R,值域是
B.函数y=f(x)是偶函数
C.函数y=f(x)是奇函数
D.函数y=f(x)在上单调递增
三、填空题
12.不等式log2(-x)<x+1的解集为________.
13.(2020·浙江台州一中质检)已知函数f(x)的图象是如图所示的曲线段OAB,其中O(0,0),A(1,2),B(3,1),则f =________;函数g(x)=f(x)-的零点的个数为________.
14.设函数f(x)=|x+a|,g(x)=x-1,对于任意的x∈R,不等式f(x)≥g(x)恒成立,则实数a的取值范围是________.
15.已知函数f(x)=若|f(x)|≥ax,则a的取值范围是________.
四、解答题
16.画出下列函数的图象.
(1)y=eln x;
(2)y=;
(3)y=|x2-2x-1|.
17.作出函数y=log2|x+1|的图象,由图象指出函数的单调区间,并说明它的图象可由函数y=log2x的图象经过怎样的变换而得到.
18.已知函数f(x)=
(1)在如图所示给定的直角坐标系内画出f(x)的图象;
(2)写出f(x)的单调递增区间;
(3)由图象指出当x取什么值时f(x)有最值.
19.已知函数f(x)=x|m-x|(x∈R),且f(4)=0.
(1)求实数m的值;
(2)作出函数f(x)的图象;
(3)若方程f(x)=a只有一个实数根,求a的取值范围.
20.已知函数f(x)=2x,x∈R.
(1)当m取何值时,方程|f(x)-2|=m有一个解?两个解?
(2)若不等式[f(x)]2+f(x)-m>0在R上恒成立,求m的取值范围.
参考答案
1.D
解析:由点(x,y)关于原点的对称点是(-x,-y),可知D正确.
2.A
解析:函数y=lg|x-1|的定义域为(-∞,1)∪(1,+∞),则排除B,D,当x=0时,y=0,排除C,故选A.
3.C
解析:因为y=x2-1与y=e|x|都是偶函数,所以f(x)=为偶函数,排除A,B,又由x→+∞时,f(x)→0,x→-∞时,f(x)→0,排除D,故选C.
4.B
解析:设P(x,y)为所求函数图象上的任意一点,它关于直线y=1对称的点是Q(x,2-y),由题意知点Q(x,2-y)在函数y=log2x的图象上,则2-y=log2x,即y=2-log2x=log2,故选B.
5.C
解析:要想由y=f(x)的图象得到y=-f(x+1)的图象,需要先将y=f(x)的图象关于x轴对称得到y=-f(x)的图象,然后向左平移一个单位长度得到y=-f(x+1)的图象,根据上述步骤可知C正确.故选C.
6.C
解析:若23x≤logax+1在上恒成立,则0<a<1,利用数形结合思想画出指数函数与对数函数图象(图略),易得loga+1≥,解得≤a<1,故选C.
7.D
解析:由函数图象知,函数的定义域为R,既不是奇函数也不是偶函数,则排除B、C,由图象知,当x=-2时,y>0,则排除A,故选D.
8. C
解析:作出函数f(x)=|x2-1|在区间(0,+∞)上的图象如图所示,
作出直线y=1,交f(x)的图象于点B,由x2-1=1可得xB=,
结合函数图象可得b的取值范围是(1,).
9.AC
解析:函数y=a-x与y=loga(a>0且a≠1)的单调性相反,所以排除B,D项;
当a>1时,可能的图象是C项;
当0
10.BCD
解析:由题意得,
当-4≤x<-2时,顶点B(x,y)的轨迹是以点A(-2,0)为圆心,2为半径的圆;
当-2≤x<2时,顶点B(x,y)的轨迹是以点(0,0)为圆心,2为半径的圆;
当2≤x<4时,顶点B(x,y)的轨迹是以点(2,0)为圆心,2为半径的圆;
当4≤x<6时,顶点B(x,y)的轨迹是以点(4,0)为圆心,2为半径的圆,与当-4≤x<-2时,B(x,y)的轨迹的形状相同.
因此函数y=f(x)在[-4,4]上的图象恰好为函数y=f(x)的一个周期的图象,所以函数y=f(x)的周期是8,作出y=f(x)在[-4,4]上的图象如图所示:
由图象及题意得,该函数为偶函数,故A错误;
因为函数y=f(x)的周期为8,所以f(x+8)=f(x),所以f(x+4)=f(x-4),故B正确;
由图象可得,该函数的值域为[0,2],故C正确;
因为该函数是以8为周期的函数,所以函数y=f(x)在区间[6,8]上的图象与在区间[-2,0]上的图象相同,所以y=f(x)在[6,8]上单调递增,故D正确.
故选BCD.
11.AD
解析:化简函数解析式可得,
f(x)=x-{x}=
画出该函数的图象,如图所示,
由图象可知A,D正确.
12.答案:(-1,0)
解析:在同一坐标系中画出函数y=log2(-x)和y=x+1的图象如图所示:
由图象知,不等式log2(-x)<x+1的解集为(-1,0).
13.答案:2 2
解析:由图可知,f(3)=1,故f =f(1)=2.
函数g(x)=f(x)-的零点的个数为函数y=f(x)与函数y=的图象的交点个数,
由图象可知,有2个交点,故零点的个数为2.
14.答案: [-1,+∞)
解析:如图,作出函数f(x)=|x+a|与g(x)=x-1的图象,
观察图象可知:当且仅当-a≤1,即a≥-1时,不等式f(x)≥g(x)恒成立,因此a的取值范围是[-1,+∞).
15.解析: [-2,0]
解析:可画出|f(x)|的图象如图所示.
当a=0时,|f(x)|≥ax=0恒成立,
所以a=0满足题意;
当a>0时,在x<0时,|f(x)|≥ax恒成立,所以只需x>0时,ln(x+1)≥ax成立.
对比对数函数与正比例函数的增长速度发现,一定存在ln(x+1)
当a<0时,在x>0时满足题意;
当x≤0时,只需x2-2x≥ax成立,
即直线在抛物线下方,即a≥x-2恒成立,则a≥-2.
综上,a的取值范围为[-2,0].
16.解: (1)因为函数的定义域为{x|x>0}且y=eln x=x(x>0),所以其图象如图①所示.
图① 图②
(2)y==1+,先作出y=的图象,将其图象向右平移1个单位,再向上平移1个单位,即得y=的图象,如图②.
(3)先作出函数y=x2-2x-1的图象,然后x轴上方的图象不变,把x轴下方的图象以x轴为对称轴,翻折到x轴上方,得到y=|x2-2x-1|的图象,如图③中实线部分.
图③
17.解:作出函数y=log2x的图象,将其关于y轴对称得到函数y=log2|x|的图象,再将图象向左平移1个单位长度就得到函数y=log2|x+1|的图象(如图所示).由图知,函数y=log2|x+1|的单调递减区间为(-∞,-1),单调递增区间为(-1,+∞).
18.解:(1)函数f(x)的图象如图所示.
(2)由图象可知,函数f(x)的单调递增区间为[-1,0],[2,5].
(3)由图象知当x=2时,f(x)min=f(2)=-1,
当x=0时,f(x)max=f(0)=3.
19.解:(1)因为f(4)=0,所以4|m-4|=0,即m=4.
(2)f(x)=x|x-4|=
f(x)的图象如图所示.
(3)由f(x)的图象可知,当a>4或a<0时,f(x)的图象与直线y=a只有一个交点,即方程f(x)=a只有一个实数根,即a的取值范围是(-∞,0)∪(4,+∞).
20.解:(1)令F(x)=|f(x)-2|=|2x-2|,G(x)=m,画出F(x)的图象如图所示,
由图象看出,当m=0或m≥2时,函数F(x)与G(x)的图象只有一个交点,原方程有一个解;
当0
因为H(t)=-在区间(0,+∞)上是增函数,
所以H(t)>H(0)=0.
因此要使t2+t>m在区间(0,+∞)上恒成立,
应有m≤0,
即m的取值范围为(-∞,0].
