人教B版(2019)数学必修第二册期中复习:函数模型及其应用达标训练(含答案)
文档属性
| 名称 | 人教B版(2019)数学必修第二册期中复习:函数模型及其应用达标训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 225.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览





文档简介
函数模型及其应用
一、单项选择题
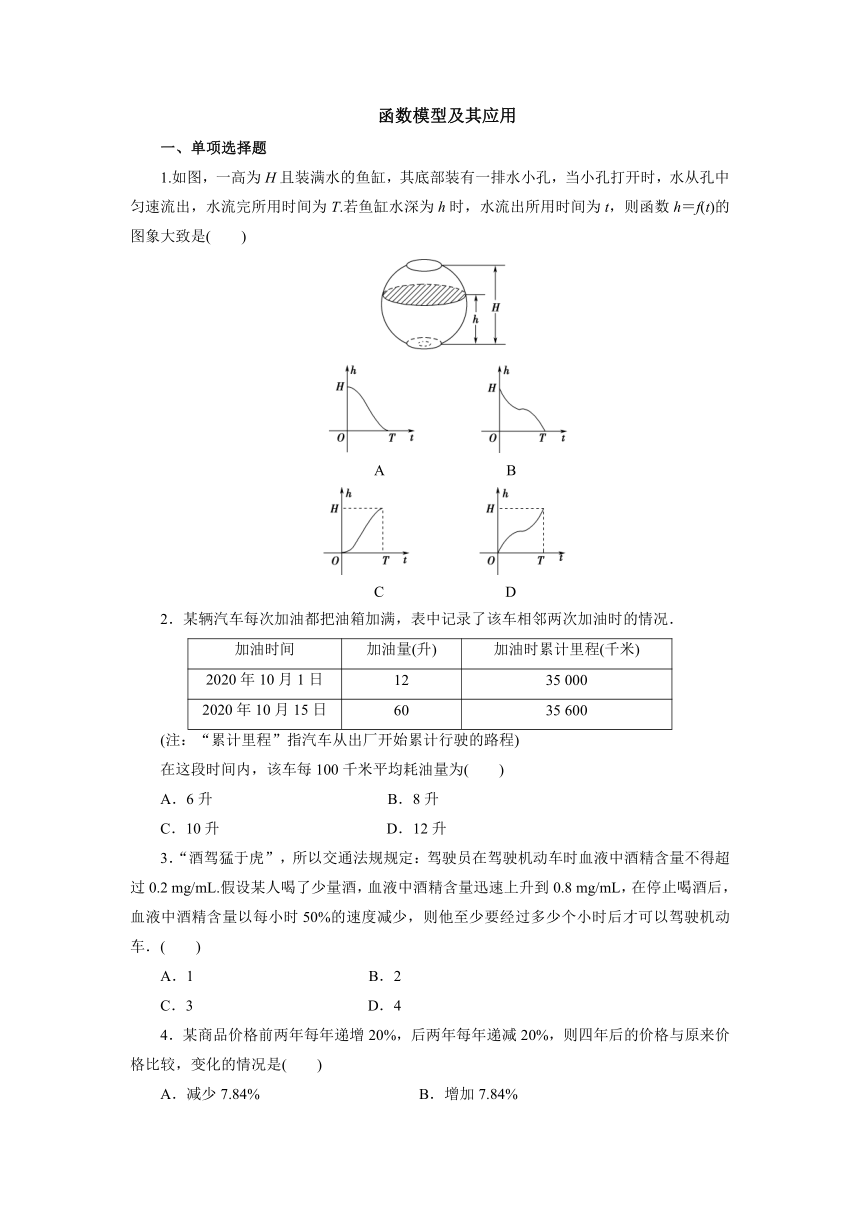
1.如图,一高为H且装满水的鱼缸,其底部装有一排水小孔,当小孔打开时,水从孔中匀速流出,水流完所用时间为T.若鱼缸水深为h时,水流出所用时间为t,则函数h=f(t)的图象大致是( )
A B
C D
2.某辆汽车每次加油都把油箱加满,表中记录了该车相邻两次加油时的情况.
加油时间 加油量(升) 加油时累计里程(千米)
2020年10月1日 12 35 000
2020年10月15日 60 35 600
(注:“累计里程”指汽车从出厂开始累计行驶的路程)
在这段时间内,该车每100千米平均耗油量为( )
A.6升 B.8升
C.10升 D.12升
3.“酒驾猛于虎”,所以交通法规规定:驾驶员在驾驶机动车时血液中酒精含量不得超过0.2 mg/mL.假设某人喝了少量酒,血液中酒精含量迅速上升到0.8 mg/mL,在停止喝酒后,血液中酒精含量以每小时50%的速度减少,则他至少要经过多少个小时后才可以驾驶机动车.( )
A.1 B.2
C.3 D.4
4.某商品价格前两年每年递增20%,后两年每年递减20%,则四年后的价格与原来价格比较,变化的情况是( )
A.减少7.84% B.增加7.84%
C.减少9.5% D.不增不减
5.(2020·辽宁五校联考)一个人以6米/秒的速度去追赶停在交通灯前的汽车,当他离汽车25米时交通灯由红变绿,汽车开始变速直线行驶(汽车与人前进方向相同),汽车在时间t秒内的路程为s=t2米,那么,此人( )
A.可在7秒内追上汽车
B.可在9秒内追上汽车
C.不能追上汽车,但期间离汽车的最近距离为14米
D.不能追上汽车,但期间离汽车的最近距离为7米
6.某公司租地建仓库,已知仓库每月占用费y1与仓库到车站的距离成反比,而每月货物的运费y2与仓库到车站的距离成正比.据测算,如果在距离车站10千米处建仓库,这两项费用y1,y2分别是2万和8万,那么要使这两项费用之和最小,仓库应建在离车站( )
A.5千米处 B.4千米处
C.3千米处 D.2千米处
7.(2020·高考全国卷Ⅲ)Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:I(t)=,其中K为最大确诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3)( )
A.60 B.63
C.66 D.69
8.我们定义函数y=[x]([x]表示不大于x的最大整数)为“下整函数”;定义y={x}({x}表示不小于x的最小整数)为“上整函数”;例如[4.3]=4,[5]=5;{4.3}=5,{5}=5.某停车场收费标准为每小时2元,即不超过1小时(包括1小时)收费2元,超过一小时,不超过2小时(包括2小时)收费4元,以此类推.若李刚停车时间为x小时,则李刚应付费为(单位:元)( )
A.2[x+1] B.2([x]+1)
C.2{x} D.{2x}
二、多项选择题
9.(2020·北京东城区一模改编)某部影片的盈利额(即影片的票房收入与固定成本之差)记为y,观影人数记为x,y关于x的函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后y关于x的函数图象.
图(1) 图(2) 图(3)
给出下列四种说法,其中正确的说法是( )
A.图(2)对应的方案是:提高票价,并提高固定成本
B.图(2)对应的方案是:保持票价不变,并降低固定成本
C.图(3)对应的方案是:提高票价,并保持固定成本不变
D.图(3)对应的方案是:提高票价,并降低固定成本
10.某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=,且该食品在4 ℃的保鲜时间是16小时.已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时刻的变化如图所示,则下列结论中正确的是( )
A.该食品在6 ℃的保鲜时间是8小时
B.当x∈[-6,6]时,该食品的保鲜时间t随着x的增大而逐渐减少
C.到了此日13时,甲所购买的食品还在保鲜时间内
D.到了此日14时,甲所购买的食品已然过了保鲜时间
11.某工厂生产一种溶液,按市场要求杂质含量不得超过0.1%,而这种溶液最初的杂质含量为2%,现进行过滤,已知每过滤一次杂质含量减少,则使产品达到市场要求的过滤次数可以为(参考数据:lg 2≈0.301,lg 3≈0.477)( )
A.6 B.9
C.8 D.7
三、填空题
12.某汽车销售公司在A,B两地销售同一种品牌的汽车,在A地的销售利润(单位:万元)为y1=4.1x-0.1x2,在B地的销售利润(单位:万元)为y2=2x,其中x为销售量(单位:辆),若该公司在两地共销售16辆该种品牌的汽车,则能获得的最大利润是________万元.
13.(2020·山东济宁期末)年7月,中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳14的质量N随时间t(单位:年)的衰变规律满足N=N0· (N0表示碳14原有的质量),则经过5730年后,碳14的质量变为原来的________;经过测定,良渚古城遗址文物样本中碳14的质量是原来的至,据此推测良渚古城存在的时期距今约在________年到5 730年之间.(参考数据:log23≈1.6,log25≈2.3)
14.(2020·洛阳模拟)为促进全民健身运动,公司为员工购买某健身俱乐部的健身卡,每张360元,使用规定:不记名,每卡每次仅限1人,每天仅限1次.公司共90名员工,公司领导打算组织员工分批去健身,除需购买若干张健身卡外,每次去俱乐部还要包租一辆汽车,费用是每次40元,如果要使每位员工健身10次,那么公司购买________张健身卡最合算.
15.(·北京高考)李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
(1)当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付________元;
(2)在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为________.
16.(2020·新高考卷Ⅰ)某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC=,BH∥DG,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
四、解答题
17.如图,已知边长为8米的正方形钢板有一个角被锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,在五边形ABCDE内截取一个矩形BNPM,使点P在边DE上.
(1)设MP=x米,PN=y米,将y表示成x的函数,并求该函数的解析式及定义域;
(2)求矩形BNPM面积的最大值.
18.某地下车库在排气扇发生故障的情况下测得空气中一氧化碳含量达到了危险状态,经抢修排气扇恢复正常.排气4分钟后测得车库内的一氧化碳浓度为64 ppm,继续排气4分钟后又测得浓度为32 ppm.由检验知该地下车库一氧化碳浓度y(ppm)与排气时间t(分钟)之间存在函数关系y=c(c,m为常数).
(1)求c,m的值;
(2)若空气中一氧化碳浓度不高于0.5 ppm为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?
19.为响应国家提出的“大众创业,万众创新”的号召,小李同学大学毕业后,决定利用所学专业进行自主创业.经过调查,生产某小型电子产品需投入年固定成本5万元,每年生产x万件,需另投入流动成本C(x)万元,且C(x)=,每件产品售价为10元,经分析,生产的产品当年能全部售完.
(1)写出年利润P(x)(万元)关于年产量x(万件)的函数解析式(年利润=年销售收入-固定成本-流动成本);
(2)年产量为多少万件时,小李在这一产品的生产中所获利润最大?最大利润是多少?
20.某种出口产品的关税税率为t,市场价格x(单位:千元)与市场供应量p(单位:万件)之间近似满足关系式:p=2(1-kt)(x-b)2,其中k,b均为常数.当关税税率t=75%时,若市场价格为5千元,则市场供应量约为1万件;若市场价格为7千元,则市场供应量约为2万件.
(1)试确定k,b的值;
(2)市场需求量q(单位:万件)与市场价格x(单位:千元)近似满足关系式:q=2-x,当p=q时,市场价格称为市场平衡价格,当市场平衡价格不超过4千元时,试确定关税税率的最大值.
21.某公司计划投资开发一种新能源产品,预计能获得10~1 000万元的收益.现准备制定一个对开发科研小组的奖励方案:资金y(单位:万元)随收益x(单位:万元)的增加而增加,且奖金总数不超过9万元,同时奖金总数不超过收益的20%.
(1)若建立奖励方案函数模型y=f(x),试确定这个函数的定义域、值域和的范围;
(2)现有两个奖励函数模型:①y=+2;②y=4lg x-3.试分析这两个函数模型是否符合公司的要求?请说明理由.
22.(2020·高考江苏卷)某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O在水平线MN上,桥AB与MN平行,OO′为铅垂线(O′在AB上).经测量,左侧曲线AO上任一点D到MN的距离h1(米)与D到OO′的距离a(米)之间满足关系式h1=a2;右侧曲线BO上任一点F到MN的距离h2(米)与F到OO′的距离b(米)之间满足关系式h2=-b3+6b.已知点B到OO′的距离为40米.
(1)求桥AB的长度;
(2)计划在谷底两侧建造平行于OO′的桥墩CD和EF,且CE为80米,其中C,E在AB上(不包括端点).桥墩EF每米造价k(万元),桥墩CD每米造价k(万元)(k>0),问O′E为多少米时,桥墩CD与EF的总造价最低?
参考答案
1.B
解析:函数h=f(t)是关于t的减函数,故排除C,D,半缸水前,h的变化是越来越慢,半缸水后,h的变化是越来越快,故选B.
2.C
解析:因为第二次加满油箱时加油量为60升,
所以从第一次加油到第二次加油共用油60升,行驶了600千米,
所以在这段时间内,该车每100千米平均耗油量为=10(升).故选C.
3.B
解析:设n个小时后才可以驾驶机动车,
则0.8×(1-50%)n=0.2.解得n=log0.5 0.25=2.
即至少要经过2个小时后才可以驾驶机动车.故选B.
4.A
解析:设某商品原来价格为a,四年后价格为:
a(1+0.2)2(1-0.2)2=a×1.22×0.82=0.921 6a,
(0.921 6-1)a=-0.078 4a,
所以四年后的价格与原来价格比较,减少7.84%.
5.D
解析:已知s=t2,车与人的间距d=(s+25)-6t=t2-6t+25=(t-6)2+7.
当t=6时,d取得最小值7.
故选D.
6.A
解析:设仓库建在离车站x千米处,则y1=,y2=k2x,
根据给出的初始数据可得k1=20,k2=0.8,
两项费用之和为y=+0.8x≥8,当且仅当x=5时,等号成立.
7.C
解析:由题意可知,当I(t*)=0.95K时,=0.95K,
即=1+e-0.23(t*-53),e-0.23(t*-53)=,e0.23(t*-53)=19,
所以0.23(t*-53)=ln 19≈3,所以t*≈66.故选C.
8.C
解析:如x=1时,应付费2元,
此时2[x+1]=4,2([x]+1)=4,排除A,B;
当x=0.5时,付费为2元,此时{2x}=1,排除D,故选C.
9.BC
解析:由图(1)可设y关于x的函数为y=kx+b,k>0,b<0,k为票价,当k=0时,y=b,则-b为固定成本.由图(2)知,直线向上平移,k不变,即票价不变,b变大,则-b变小,固定成本减小,故A错误,B正确;由图(3)知,直线与y轴的交点不变,直线斜率变大,即k变大,票价提高,b不变,即-b不变,固定成本不变,故C正确,D错误.故答案为BC.
10.AD
解析:因为食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=,且该食品在4℃的保鲜时间是16小时,所以,即4k+6=4,解得k=,所以t=,
当x=6时,t=8,A项中该食品在6 ℃的保鲜时间是8小时,正确;
B项中,当x∈[-6,0]时,保鲜时间恒为64小时,当x∈[0,6]时,该食品的保鲜时间t随着x的增大而逐渐减少,故错误;
C项中,到了此日11时,温度超过11度,此时保鲜时间不超过2小时,故到13时,甲所购买的食品不在保鲜时间内,故错误;
D项中,到了此日14时,甲所购买的食品已然过了保鲜时间,故正确,
故选A, D.
11.BC
解析:设经过n次过滤,产品达到市场要求,则×n≤,即n≤.
由nlg≤-lg 20.
即n(lg 2-ln 3)≤-(1+lg 2),即n≥≈7.4,
所以选B、C.
12.答案:43
解析:设公司在A地销售该品牌的汽车x(0≤x≤16且x∈N*)辆,则在B地销售该品牌的汽车(16-x)辆,
所以可得利润y=4.1x-0.1x2+2(16-x)=-0.1x2+2.1x+32=-×2+×+32.
因为x∈[0,16]且x∈N*,
所以当x=10或11时,总利润取得最大值43万元.
13.答案: 4 011
解析:当t=5 730时,N=N0·2-1=N0,
∴经过5 730年后,碳14的质量变为原来的.令N=N0,则=,
∴-=log2=log23-log25≈-0.7,
∴t≈0.7×5 730=4 011,
∴良渚古城存在的时期距今约在4 011年到5 730年之间.
14.答案:10
解析:设购买x张健身卡,这项健身活动的总支出为y,
则y=×40+360x,
即y=360≥360×2=7 200,
当且仅当=x,即x=10时取等号,
所以公司购买10张健身卡最合算.
15.答案:(1)130 (2)15
解析:(1)顾客一次购买草莓和西瓜各1盒时,总价为60+80=140(元),总价达到120元,又x=10,即顾客少付10元,所以需要支付130元.
(2)设顾客买水果的总价为a元,当0≤a<120时,顾客支付a元,李明得到0.8a元,且0.8a≥0.7a,显然符合题意,此时x=0;当a≥120时,则0.8(a-x)≥0.7a恒成立,即x≤a恒成立,x≤min,又a≥120,所以min=15所以x≤15.
综上可知,0≤x≤15.所以x的最大值为15.
16.答案:+4
解析:如图,连接OA,作AQ⊥DE,交ED的延长线于Q,AM⊥EF于M,交DG于E′,交BH于F′,记过O且垂直于DG的直线与DG的交点为P,设OP=3m,则DP=5m,不难得出AQ=7,AM=7,于是AE′=5,E′G=5,所以∠AGE′=∠AHF′=,△AOH为等腰直角三角形,又AF′=5-3m,OF′=7-5m,AF′=OF′,所以5-3m=7-5m,得m=1,所以AF′=5-3m=2,OF′=7-5m=2,所以OA=2,则阴影部分的面积S=×π×(2)2+×2×2-=(cm2).
17.解:(1)如图,作PQ⊥AF于Q,所以PQ=8-y,EQ=x-4,
在△EDF中,=,
所以=,
所以y=-x+10,
定义域为{x|4≤x≤8}.
(2)设矩形BNPM的面积为S,
则S(x)=xy=x=-(x-10)2+50,
所以S(x)是关于x的二次函数,且其图象开口向下,对称轴为直线x=10,
所以当x∈[4,8]时,S(x)单调递增,
所以当x=8时,矩形BNPM的面积取得最大值,最大值为48平方米.
18.解:(1)由题意可列方程组
两式相除,解得
(2)由题意可列不等式128≤0.5,
所以≤,即t≥8,解得t≥32.
故至少排气32分钟,这个地下车库中的一氧化碳含量才能达到正常状态.
19.解:(1)因为每件产品售价为10元,所以x万件产品销售收入为10x万元.
依题意得,当0<x<8时,P(x)=10x--5=-x2+6x-5;
当x≥8时,P(x)=10x--5=30-.
所以P(x)=
(2)当0<x<8时,P(x)=-(x-6)2+13,当x=6时,P(x)取得最大值P(6)=13;
当x≥8时,P′(x)=-1+<0,所以P(x)为减函数,
当x=8时,P(x)取得最大值P(8)=.
由13<可知当年产量为8万件时,小李在这一产品的生产中所获利润最大,最大利润为万元.
20.解:(1)由已知得:
解得b=5,k=1.
(2)当p=q时,2(1-t)(x-5) 2=2-x,
所以(1-t)(x-5)2=-x t=1+=1+.
而f(x)=x+在(0,4]上单调递减,
所以当x=4时,f(x)有最小值,
故当x=4时,关税税率的最大值为500%.
21.解:(1)y=f(x)的定义域是[10,1 000],值域是(0,9],∈(0,0.2].
(2)①不符合,②符合.理由如下:
当y=+2时,=+的最大值是>0.2,不符合公司的要求.
当y=4lg x-3时,函数在定义域上为增函数,最大值为9.
由≤0.2可知y-0.2x≤0.
令g(x)=4lg x-3-0.2x,x∈[10,1 000],则g′(x)=<0,所以g(x)在[10,1 000]上单调递减,所以g(x)≤g(10)=-1<0,即≤0.2.故函数y=4lg x-3符合公司的要求.
22.解:(1)设AA1,BB1,CD1,EF1都与MN垂直,A1,B1,D1,F1是相应垂足.
由条件知,当O′B =40时,
BB1=-×403+6×40=160,则AA1=160.
由O′A2=160,得O′A=80.
所以AB=O′A+O′B=80+40= 120(米).
(2)以O为原点,OO′为y轴建立平面直角坐标系xOy(如图所示).
设F(x,y2),x∈(0,40),
则y2=-x3+6x,
EF=160-y2=160+x3-6x.
因为CE =80,所以O′C=80-x,
设D(x-80,y1),则y1=( 80-x)2,
所以CD= 160-y1=160-(80-x)2=-x2 +4x.
记桥墩CD和EF的总造价为f(x),
则f(x)=k+k
=k(0f′(x)=k=x(x-20),
令f′(x)=0,得x=20.
x (0,20) 20 (20,40)
f′(x) - 0 +
f(x) ? 极小值 ?
所以当x=20时,f(x)取得最小值.
答:(1)桥AB的长度为120米;
(2)当O′E为20米时,桥墩CD和EF的总造价最低.
一、单项选择题
1.如图,一高为H且装满水的鱼缸,其底部装有一排水小孔,当小孔打开时,水从孔中匀速流出,水流完所用时间为T.若鱼缸水深为h时,水流出所用时间为t,则函数h=f(t)的图象大致是( )
A B
C D
2.某辆汽车每次加油都把油箱加满,表中记录了该车相邻两次加油时的情况.
加油时间 加油量(升) 加油时累计里程(千米)
2020年10月1日 12 35 000
2020年10月15日 60 35 600
(注:“累计里程”指汽车从出厂开始累计行驶的路程)
在这段时间内,该车每100千米平均耗油量为( )
A.6升 B.8升
C.10升 D.12升
3.“酒驾猛于虎”,所以交通法规规定:驾驶员在驾驶机动车时血液中酒精含量不得超过0.2 mg/mL.假设某人喝了少量酒,血液中酒精含量迅速上升到0.8 mg/mL,在停止喝酒后,血液中酒精含量以每小时50%的速度减少,则他至少要经过多少个小时后才可以驾驶机动车.( )
A.1 B.2
C.3 D.4
4.某商品价格前两年每年递增20%,后两年每年递减20%,则四年后的价格与原来价格比较,变化的情况是( )
A.减少7.84% B.增加7.84%
C.减少9.5% D.不增不减
5.(2020·辽宁五校联考)一个人以6米/秒的速度去追赶停在交通灯前的汽车,当他离汽车25米时交通灯由红变绿,汽车开始变速直线行驶(汽车与人前进方向相同),汽车在时间t秒内的路程为s=t2米,那么,此人( )
A.可在7秒内追上汽车
B.可在9秒内追上汽车
C.不能追上汽车,但期间离汽车的最近距离为14米
D.不能追上汽车,但期间离汽车的最近距离为7米
6.某公司租地建仓库,已知仓库每月占用费y1与仓库到车站的距离成反比,而每月货物的运费y2与仓库到车站的距离成正比.据测算,如果在距离车站10千米处建仓库,这两项费用y1,y2分别是2万和8万,那么要使这两项费用之和最小,仓库应建在离车站( )
A.5千米处 B.4千米处
C.3千米处 D.2千米处
7.(2020·高考全国卷Ⅲ)Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:I(t)=,其中K为最大确诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3)( )
A.60 B.63
C.66 D.69
8.我们定义函数y=[x]([x]表示不大于x的最大整数)为“下整函数”;定义y={x}({x}表示不小于x的最小整数)为“上整函数”;例如[4.3]=4,[5]=5;{4.3}=5,{5}=5.某停车场收费标准为每小时2元,即不超过1小时(包括1小时)收费2元,超过一小时,不超过2小时(包括2小时)收费4元,以此类推.若李刚停车时间为x小时,则李刚应付费为(单位:元)( )
A.2[x+1] B.2([x]+1)
C.2{x} D.{2x}
二、多项选择题
9.(2020·北京东城区一模改编)某部影片的盈利额(即影片的票房收入与固定成本之差)记为y,观影人数记为x,y关于x的函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后y关于x的函数图象.
图(1) 图(2) 图(3)
给出下列四种说法,其中正确的说法是( )
A.图(2)对应的方案是:提高票价,并提高固定成本
B.图(2)对应的方案是:保持票价不变,并降低固定成本
C.图(3)对应的方案是:提高票价,并保持固定成本不变
D.图(3)对应的方案是:提高票价,并降低固定成本
10.某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=,且该食品在4 ℃的保鲜时间是16小时.已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时刻的变化如图所示,则下列结论中正确的是( )
A.该食品在6 ℃的保鲜时间是8小时
B.当x∈[-6,6]时,该食品的保鲜时间t随着x的增大而逐渐减少
C.到了此日13时,甲所购买的食品还在保鲜时间内
D.到了此日14时,甲所购买的食品已然过了保鲜时间
11.某工厂生产一种溶液,按市场要求杂质含量不得超过0.1%,而这种溶液最初的杂质含量为2%,现进行过滤,已知每过滤一次杂质含量减少,则使产品达到市场要求的过滤次数可以为(参考数据:lg 2≈0.301,lg 3≈0.477)( )
A.6 B.9
C.8 D.7
三、填空题
12.某汽车销售公司在A,B两地销售同一种品牌的汽车,在A地的销售利润(单位:万元)为y1=4.1x-0.1x2,在B地的销售利润(单位:万元)为y2=2x,其中x为销售量(单位:辆),若该公司在两地共销售16辆该种品牌的汽车,则能获得的最大利润是________万元.
13.(2020·山东济宁期末)年7月,中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳14的质量N随时间t(单位:年)的衰变规律满足N=N0· (N0表示碳14原有的质量),则经过5730年后,碳14的质量变为原来的________;经过测定,良渚古城遗址文物样本中碳14的质量是原来的至,据此推测良渚古城存在的时期距今约在________年到5 730年之间.(参考数据:log23≈1.6,log25≈2.3)
14.(2020·洛阳模拟)为促进全民健身运动,公司为员工购买某健身俱乐部的健身卡,每张360元,使用规定:不记名,每卡每次仅限1人,每天仅限1次.公司共90名员工,公司领导打算组织员工分批去健身,除需购买若干张健身卡外,每次去俱乐部还要包租一辆汽车,费用是每次40元,如果要使每位员工健身10次,那么公司购买________张健身卡最合算.
15.(·北京高考)李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
(1)当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付________元;
(2)在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为________.
16.(2020·新高考卷Ⅰ)某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC=,BH∥DG,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
四、解答题
17.如图,已知边长为8米的正方形钢板有一个角被锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,在五边形ABCDE内截取一个矩形BNPM,使点P在边DE上.
(1)设MP=x米,PN=y米,将y表示成x的函数,并求该函数的解析式及定义域;
(2)求矩形BNPM面积的最大值.
18.某地下车库在排气扇发生故障的情况下测得空气中一氧化碳含量达到了危险状态,经抢修排气扇恢复正常.排气4分钟后测得车库内的一氧化碳浓度为64 ppm,继续排气4分钟后又测得浓度为32 ppm.由检验知该地下车库一氧化碳浓度y(ppm)与排气时间t(分钟)之间存在函数关系y=c(c,m为常数).
(1)求c,m的值;
(2)若空气中一氧化碳浓度不高于0.5 ppm为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?
19.为响应国家提出的“大众创业,万众创新”的号召,小李同学大学毕业后,决定利用所学专业进行自主创业.经过调查,生产某小型电子产品需投入年固定成本5万元,每年生产x万件,需另投入流动成本C(x)万元,且C(x)=,每件产品售价为10元,经分析,生产的产品当年能全部售完.
(1)写出年利润P(x)(万元)关于年产量x(万件)的函数解析式(年利润=年销售收入-固定成本-流动成本);
(2)年产量为多少万件时,小李在这一产品的生产中所获利润最大?最大利润是多少?
20.某种出口产品的关税税率为t,市场价格x(单位:千元)与市场供应量p(单位:万件)之间近似满足关系式:p=2(1-kt)(x-b)2,其中k,b均为常数.当关税税率t=75%时,若市场价格为5千元,则市场供应量约为1万件;若市场价格为7千元,则市场供应量约为2万件.
(1)试确定k,b的值;
(2)市场需求量q(单位:万件)与市场价格x(单位:千元)近似满足关系式:q=2-x,当p=q时,市场价格称为市场平衡价格,当市场平衡价格不超过4千元时,试确定关税税率的最大值.
21.某公司计划投资开发一种新能源产品,预计能获得10~1 000万元的收益.现准备制定一个对开发科研小组的奖励方案:资金y(单位:万元)随收益x(单位:万元)的增加而增加,且奖金总数不超过9万元,同时奖金总数不超过收益的20%.
(1)若建立奖励方案函数模型y=f(x),试确定这个函数的定义域、值域和的范围;
(2)现有两个奖励函数模型:①y=+2;②y=4lg x-3.试分析这两个函数模型是否符合公司的要求?请说明理由.
22.(2020·高考江苏卷)某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O在水平线MN上,桥AB与MN平行,OO′为铅垂线(O′在AB上).经测量,左侧曲线AO上任一点D到MN的距离h1(米)与D到OO′的距离a(米)之间满足关系式h1=a2;右侧曲线BO上任一点F到MN的距离h2(米)与F到OO′的距离b(米)之间满足关系式h2=-b3+6b.已知点B到OO′的距离为40米.
(1)求桥AB的长度;
(2)计划在谷底两侧建造平行于OO′的桥墩CD和EF,且CE为80米,其中C,E在AB上(不包括端点).桥墩EF每米造价k(万元),桥墩CD每米造价k(万元)(k>0),问O′E为多少米时,桥墩CD与EF的总造价最低?
参考答案
1.B
解析:函数h=f(t)是关于t的减函数,故排除C,D,半缸水前,h的变化是越来越慢,半缸水后,h的变化是越来越快,故选B.
2.C
解析:因为第二次加满油箱时加油量为60升,
所以从第一次加油到第二次加油共用油60升,行驶了600千米,
所以在这段时间内,该车每100千米平均耗油量为=10(升).故选C.
3.B
解析:设n个小时后才可以驾驶机动车,
则0.8×(1-50%)n=0.2.解得n=log0.5 0.25=2.
即至少要经过2个小时后才可以驾驶机动车.故选B.
4.A
解析:设某商品原来价格为a,四年后价格为:
a(1+0.2)2(1-0.2)2=a×1.22×0.82=0.921 6a,
(0.921 6-1)a=-0.078 4a,
所以四年后的价格与原来价格比较,减少7.84%.
5.D
解析:已知s=t2,车与人的间距d=(s+25)-6t=t2-6t+25=(t-6)2+7.
当t=6时,d取得最小值7.
故选D.
6.A
解析:设仓库建在离车站x千米处,则y1=,y2=k2x,
根据给出的初始数据可得k1=20,k2=0.8,
两项费用之和为y=+0.8x≥8,当且仅当x=5时,等号成立.
7.C
解析:由题意可知,当I(t*)=0.95K时,=0.95K,
即=1+e-0.23(t*-53),e-0.23(t*-53)=,e0.23(t*-53)=19,
所以0.23(t*-53)=ln 19≈3,所以t*≈66.故选C.
8.C
解析:如x=1时,应付费2元,
此时2[x+1]=4,2([x]+1)=4,排除A,B;
当x=0.5时,付费为2元,此时{2x}=1,排除D,故选C.
9.BC
解析:由图(1)可设y关于x的函数为y=kx+b,k>0,b<0,k为票价,当k=0时,y=b,则-b为固定成本.由图(2)知,直线向上平移,k不变,即票价不变,b变大,则-b变小,固定成本减小,故A错误,B正确;由图(3)知,直线与y轴的交点不变,直线斜率变大,即k变大,票价提高,b不变,即-b不变,固定成本不变,故C正确,D错误.故答案为BC.
10.AD
解析:因为食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=,且该食品在4℃的保鲜时间是16小时,所以,即4k+6=4,解得k=,所以t=,
当x=6时,t=8,A项中该食品在6 ℃的保鲜时间是8小时,正确;
B项中,当x∈[-6,0]时,保鲜时间恒为64小时,当x∈[0,6]时,该食品的保鲜时间t随着x的增大而逐渐减少,故错误;
C项中,到了此日11时,温度超过11度,此时保鲜时间不超过2小时,故到13时,甲所购买的食品不在保鲜时间内,故错误;
D项中,到了此日14时,甲所购买的食品已然过了保鲜时间,故正确,
故选A, D.
11.BC
解析:设经过n次过滤,产品达到市场要求,则×n≤,即n≤.
由nlg≤-lg 20.
即n(lg 2-ln 3)≤-(1+lg 2),即n≥≈7.4,
所以选B、C.
12.答案:43
解析:设公司在A地销售该品牌的汽车x(0≤x≤16且x∈N*)辆,则在B地销售该品牌的汽车(16-x)辆,
所以可得利润y=4.1x-0.1x2+2(16-x)=-0.1x2+2.1x+32=-×2+×+32.
因为x∈[0,16]且x∈N*,
所以当x=10或11时,总利润取得最大值43万元.
13.答案: 4 011
解析:当t=5 730时,N=N0·2-1=N0,
∴经过5 730年后,碳14的质量变为原来的.令N=N0,则=,
∴-=log2=log23-log25≈-0.7,
∴t≈0.7×5 730=4 011,
∴良渚古城存在的时期距今约在4 011年到5 730年之间.
14.答案:10
解析:设购买x张健身卡,这项健身活动的总支出为y,
则y=×40+360x,
即y=360≥360×2=7 200,
当且仅当=x,即x=10时取等号,
所以公司购买10张健身卡最合算.
15.答案:(1)130 (2)15
解析:(1)顾客一次购买草莓和西瓜各1盒时,总价为60+80=140(元),总价达到120元,又x=10,即顾客少付10元,所以需要支付130元.
(2)设顾客买水果的总价为a元,当0≤a<120时,顾客支付a元,李明得到0.8a元,且0.8a≥0.7a,显然符合题意,此时x=0;当a≥120时,则0.8(a-x)≥0.7a恒成立,即x≤a恒成立,x≤min,又a≥120,所以min=15所以x≤15.
综上可知,0≤x≤15.所以x的最大值为15.
16.答案:+4
解析:如图,连接OA,作AQ⊥DE,交ED的延长线于Q,AM⊥EF于M,交DG于E′,交BH于F′,记过O且垂直于DG的直线与DG的交点为P,设OP=3m,则DP=5m,不难得出AQ=7,AM=7,于是AE′=5,E′G=5,所以∠AGE′=∠AHF′=,△AOH为等腰直角三角形,又AF′=5-3m,OF′=7-5m,AF′=OF′,所以5-3m=7-5m,得m=1,所以AF′=5-3m=2,OF′=7-5m=2,所以OA=2,则阴影部分的面积S=×π×(2)2+×2×2-=(cm2).
17.解:(1)如图,作PQ⊥AF于Q,所以PQ=8-y,EQ=x-4,
在△EDF中,=,
所以=,
所以y=-x+10,
定义域为{x|4≤x≤8}.
(2)设矩形BNPM的面积为S,
则S(x)=xy=x=-(x-10)2+50,
所以S(x)是关于x的二次函数,且其图象开口向下,对称轴为直线x=10,
所以当x∈[4,8]时,S(x)单调递增,
所以当x=8时,矩形BNPM的面积取得最大值,最大值为48平方米.
18.解:(1)由题意可列方程组
两式相除,解得
(2)由题意可列不等式128≤0.5,
所以≤,即t≥8,解得t≥32.
故至少排气32分钟,这个地下车库中的一氧化碳含量才能达到正常状态.
19.解:(1)因为每件产品售价为10元,所以x万件产品销售收入为10x万元.
依题意得,当0<x<8时,P(x)=10x--5=-x2+6x-5;
当x≥8时,P(x)=10x--5=30-.
所以P(x)=
(2)当0<x<8时,P(x)=-(x-6)2+13,当x=6时,P(x)取得最大值P(6)=13;
当x≥8时,P′(x)=-1+<0,所以P(x)为减函数,
当x=8时,P(x)取得最大值P(8)=.
由13<可知当年产量为8万件时,小李在这一产品的生产中所获利润最大,最大利润为万元.
20.解:(1)由已知得:
解得b=5,k=1.
(2)当p=q时,2(1-t)(x-5) 2=2-x,
所以(1-t)(x-5)2=-x t=1+=1+.
而f(x)=x+在(0,4]上单调递减,
所以当x=4时,f(x)有最小值,
故当x=4时,关税税率的最大值为500%.
21.解:(1)y=f(x)的定义域是[10,1 000],值域是(0,9],∈(0,0.2].
(2)①不符合,②符合.理由如下:
当y=+2时,=+的最大值是>0.2,不符合公司的要求.
当y=4lg x-3时,函数在定义域上为增函数,最大值为9.
由≤0.2可知y-0.2x≤0.
令g(x)=4lg x-3-0.2x,x∈[10,1 000],则g′(x)=<0,所以g(x)在[10,1 000]上单调递减,所以g(x)≤g(10)=-1<0,即≤0.2.故函数y=4lg x-3符合公司的要求.
22.解:(1)设AA1,BB1,CD1,EF1都与MN垂直,A1,B1,D1,F1是相应垂足.
由条件知,当O′B =40时,
BB1=-×403+6×40=160,则AA1=160.
由O′A2=160,得O′A=80.
所以AB=O′A+O′B=80+40= 120(米).
(2)以O为原点,OO′为y轴建立平面直角坐标系xOy(如图所示).
设F(x,y2),x∈(0,40),
则y2=-x3+6x,
EF=160-y2=160+x3-6x.
因为CE =80,所以O′C=80-x,
设D(x-80,y1),则y1=( 80-x)2,
所以CD= 160-y1=160-(80-x)2=-x2 +4x.
记桥墩CD和EF的总造价为f(x),
则f(x)=k+k
=k(0
令f′(x)=0,得x=20.
x (0,20) 20 (20,40)
f′(x) - 0 +
f(x) ? 极小值 ?
所以当x=20时,f(x)取得最小值.
答:(1)桥AB的长度为120米;
(2)当O′E为20米时,桥墩CD和EF的总造价最低.
