人教B版(2019)数学必修第三册7_2_2 单位圆与三角函数线探究案(含答案)
文档属性
| 名称 | 人教B版(2019)数学必修第三册7_2_2 单位圆与三角函数线探究案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 18:14:57 | ||
图片预览


文档简介
7.2.2 单位圆与三角函数线
探究一 作出三角函数线
作三角函数线的题型主要有两种:
(1)已知角的大小,作三角函数线,此类题型只需按步骤进行即可;
(2)已知函数值的大小找角,先找出相应y或x的值,再找出相应的角.
【例1】 在单位圆中画出适合下列条件的角α的终边.
(1)sin α=; (2)cos α=-; (3)tan α=2.
探究二 利用三角函数线比较大小
利用三角函数线比较大小,先要作出相应的三角函数线,然后观察三角函数线的大小和方向.
【例2】 若θ∈,则下列各式错误的是________.(填序号)
①sin θ+cos θ<0; ②sin θ-cos θ>0; ③|sin θ|<|cos θ|; ④sin θ+cos θ>0.
探究三 利用三角函数线解不等式
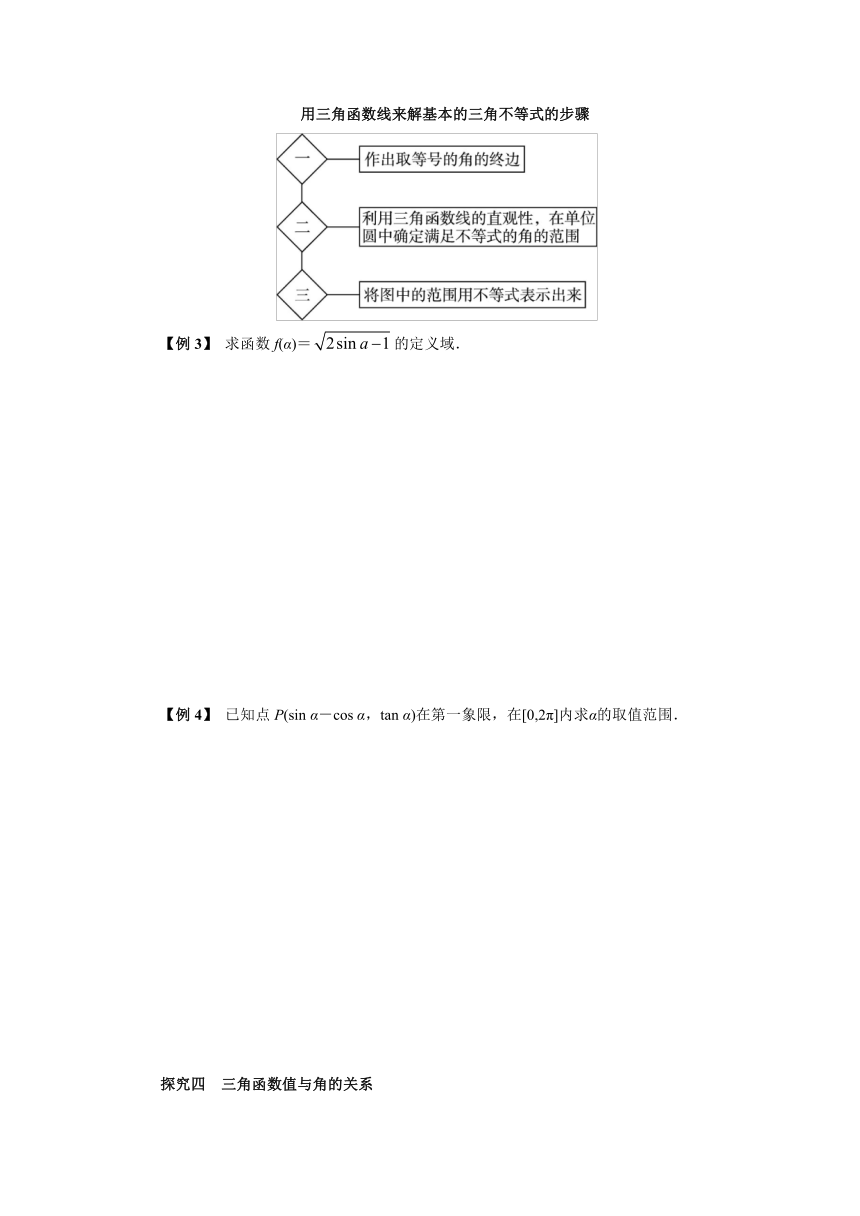
用三角函数线来解基本的三角不等式的步骤
【例3】 求函数f(α)=的定义域.
【例4】 已知点P(sin α-cos α,tan α)在第一象限,在[0,2π]内求α的取值范围.
探究四 三角函数值与角的关系
由三角函数定义知:-1≤sin α≤1,-1≤cos α≤1,即三角函数值是一个数值,而由弧度制知,数值与角也是一一对应的,如1 rad=.
【例5】 (1)若角θ在第四象限,试判断sin(cos θ)·cos(sin θ)的符号.
(2)若tan(cos θ)·cot(sin θ)>0,试指出θ所在象限.
探究五 易错辨析
易错点:因忽视角的终边在坐标轴上而致误
【例6】 利用三角函数线证明|sin α|+|cos α|≥1.
参考答案
【例1】 解析:(1)作直线y=交单位圆于点P,Q,则OP与OQ为角α的终边,如图①.
(2)作直线x=-交单位圆于点M,N,则OM与ON为角α的终边,如图②.
(3)在直线x=1上截取AT=2,其中A的坐标为(1,0).设直线OT与单位圆交于点C,D,则OC与OD为角α的终边,如图③.
【例2】 解析:画出单位圆如图所示,借助三角函数线进行判断.
由图可观察出,当θ∈时,
sin θ>0,cos θ<0,且|sin θ|<|cos θ|.
所以①②③正确,④错误.
答案:④
【例3】 解析:要使函数f(α)有意义,必须使2sin α-1≥0,则sin α≥,如图所示,画出单位圆,作x轴的平行直线y=,交单位圆于两点P1,P2,连接OP1,OP2,分别过点P1,P2作x轴的垂线,画出如图的两条正弦线,易知这两条正弦线的值都等于.
在[0,2π)内,sin =sin =.
由于sin α≥,故满足条件的角α的终边在图中阴影部分,
所以函数f(α)的定义域为.
【例4】 解析:由题意,知如图所示,
由三角函数线可得
故<α<或π<α<.
【例5】解析:(1)因为角θ在第四象限,
所以0所以sin(cos θ)>0,cos(sin θ)>0.
所以sin(cos θ)·cos(sin θ)>0.
(2)由题意,知或
所以或
即θ在第一或第三象限.
【例6】错解:证明:如图所示,MP=|sin α|,OM=|cos α|.
根据三角形中两边之和大于第三边,易知|sin α|+|cos α|≥1.
错因分析:上述解法忽视了角α的终边在坐标轴上的情况,并且正弦线、余弦线是有方向的,不能写成MP=|sin α|和OM=|cos α|.
正解:证明:当角α的终边在x(或y)轴上时,正弦线(或余弦线)变成一个点,而余弦线(或正弦线)的长等于r(r=1),所以|sin α|+|cos α|=1.当角α的终边落在四个象限时,如图,利用三角形两边之和大于第三边,有|sin α|+|cos α|=|MP|+|OM|>1.
综上,有|sin α|+|cos α|≥1.
探究一 作出三角函数线
作三角函数线的题型主要有两种:
(1)已知角的大小,作三角函数线,此类题型只需按步骤进行即可;
(2)已知函数值的大小找角,先找出相应y或x的值,再找出相应的角.
【例1】 在单位圆中画出适合下列条件的角α的终边.
(1)sin α=; (2)cos α=-; (3)tan α=2.
探究二 利用三角函数线比较大小
利用三角函数线比较大小,先要作出相应的三角函数线,然后观察三角函数线的大小和方向.
【例2】 若θ∈,则下列各式错误的是________.(填序号)
①sin θ+cos θ<0; ②sin θ-cos θ>0; ③|sin θ|<|cos θ|; ④sin θ+cos θ>0.
探究三 利用三角函数线解不等式
用三角函数线来解基本的三角不等式的步骤
【例3】 求函数f(α)=的定义域.
【例4】 已知点P(sin α-cos α,tan α)在第一象限,在[0,2π]内求α的取值范围.
探究四 三角函数值与角的关系
由三角函数定义知:-1≤sin α≤1,-1≤cos α≤1,即三角函数值是一个数值,而由弧度制知,数值与角也是一一对应的,如1 rad=.
【例5】 (1)若角θ在第四象限,试判断sin(cos θ)·cos(sin θ)的符号.
(2)若tan(cos θ)·cot(sin θ)>0,试指出θ所在象限.
探究五 易错辨析
易错点:因忽视角的终边在坐标轴上而致误
【例6】 利用三角函数线证明|sin α|+|cos α|≥1.
参考答案
【例1】 解析:(1)作直线y=交单位圆于点P,Q,则OP与OQ为角α的终边,如图①.
(2)作直线x=-交单位圆于点M,N,则OM与ON为角α的终边,如图②.
(3)在直线x=1上截取AT=2,其中A的坐标为(1,0).设直线OT与单位圆交于点C,D,则OC与OD为角α的终边,如图③.
【例2】 解析:画出单位圆如图所示,借助三角函数线进行判断.
由图可观察出,当θ∈时,
sin θ>0,cos θ<0,且|sin θ|<|cos θ|.
所以①②③正确,④错误.
答案:④
【例3】 解析:要使函数f(α)有意义,必须使2sin α-1≥0,则sin α≥,如图所示,画出单位圆,作x轴的平行直线y=,交单位圆于两点P1,P2,连接OP1,OP2,分别过点P1,P2作x轴的垂线,画出如图的两条正弦线,易知这两条正弦线的值都等于.
在[0,2π)内,sin =sin =.
由于sin α≥,故满足条件的角α的终边在图中阴影部分,
所以函数f(α)的定义域为.
【例4】 解析:由题意,知如图所示,
由三角函数线可得
故<α<或π<α<.
【例5】解析:(1)因为角θ在第四象限,
所以0
所以sin(cos θ)·cos(sin θ)>0.
(2)由题意,知或
所以或
即θ在第一或第三象限.
【例6】错解:证明:如图所示,MP=|sin α|,OM=|cos α|.
根据三角形中两边之和大于第三边,易知|sin α|+|cos α|≥1.
错因分析:上述解法忽视了角α的终边在坐标轴上的情况,并且正弦线、余弦线是有方向的,不能写成MP=|sin α|和OM=|cos α|.
正解:证明:当角α的终边在x(或y)轴上时,正弦线(或余弦线)变成一个点,而余弦线(或正弦线)的长等于r(r=1),所以|sin α|+|cos α|=1.当角α的终边落在四个象限时,如图,利用三角形两边之和大于第三边,有|sin α|+|cos α|=|MP|+|OM|>1.
综上,有|sin α|+|cos α|≥1.
