人教B版(2019)数学必修第三册向量的数量积难点突破导学案(含答案)
文档属性
| 名称 | 人教B版(2019)数学必修第三册向量的数量积难点突破导学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 314.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 20:59:02 | ||
图片预览


文档简介
向量的数量积难点突破
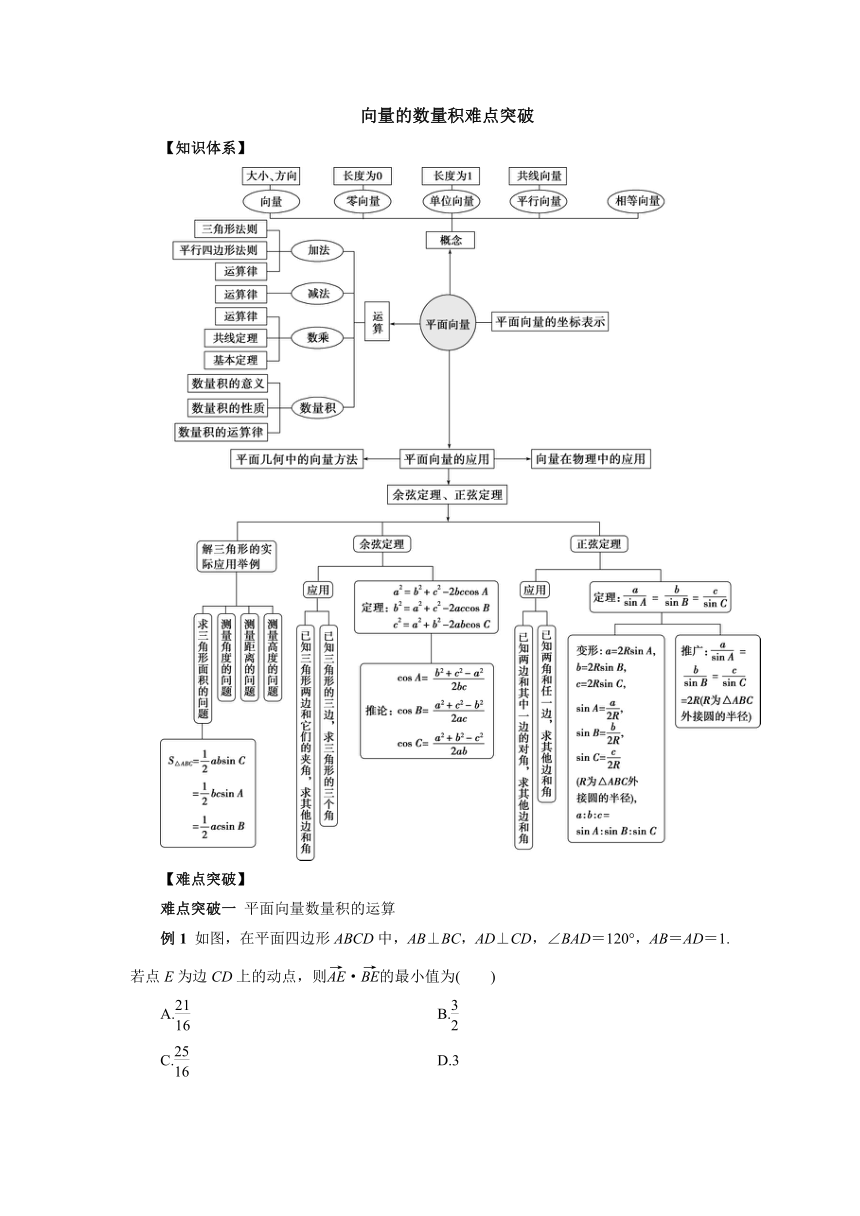
【知识体系】
【难点突破】
难点突破一 平面向量数量积的运算
例1 如图,在平面四边形ABCD中,AB⊥BC,AD⊥CD,∠BAD=120°,AB=AD=1.若点E为边CD上的动点,则·的最小值为( )
A. B.
C. D.3
[方法技巧]
向量数量积的两种计算方法
(1)当已知向量的模和夹角θ时,可利用定义法求解,即a·b=|a||b|cos θ.
(2)当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.
[强化训练]
1、已知向量a,b的夹角为,|a|=,|b|=2,则a·(a-2b)=________.
2、设四边形ABCD为平行四边形,||=6,||=4,若点M,N满足=3,=2,则·等于________.
难点突破二 向量的夹角及垂直问题
例2 (1)已知向量m=(λ+1,1),n=(λ+2,2),若(m+n)⊥(m-n),则λ=( )
A.-4 B.-3
C.-2 D.-1
(2)已知a+b+c=0,|a|=2,|b|=3,|c|=,则向量a与b的夹角为( )
A.30° B.45°
C.60° D.以上都不对
[方法技巧]
解决两个向量垂直问题,其关键在于将问题转化为它们的数量积为零,与求夹角一样.若向量能用坐标表示(或能建立适当的直角坐标系),将它转化为“x1x2+y1y2=0”较为简单.
[强化训练]
1、设向量a=(1,0),b=(-1,m).若a⊥(ma-b),则m=________.
2、已知非零向量a,b满足|a-b|=|a|,a·(a-b)=0,则a-b与b夹角的大小为________.
难点突破三 向量的长度(模)与距离的问题
例3 已知平面向量a,b的夹角为,且|a|=,|b|=2,在△ABC中,=2a+2b,=2a-6b,D为BC的中点,则||等于( )
A.2 B.4
C.6 D.8
[方法技巧]
解决向量模的问题常用的策略
(1)应用公式:|a|=(其中a=(x,y)).
(2)应用三角形法则或平行四边形法则.
(3)应用向量不等式||a|-|b||≤|a±b|≤|a|+|b|.
(4)研究模的平方|a±b|2=(a±b)2.
[强化训练]
1、已知平面向量a,b的夹角为,且a·(a-b)=8,|a|=2,则|b|等于( )
A. B.2
C.3 D.4
参考答案
例1【解析】 以A为坐标原点,AB所在直线为x轴,建立如图的平面直角坐标系,
因为在平面四边形ABCD中,AB=AD=1,∠BAD=120°,所以A(0,0),B(1,0),D,设C(1,m),E(x,y),所以=,=,
因为AD⊥CD,所以·=0,即×+=0,解得m=,即C(1,),因为E在CD上,所以≤y≤,由∥,得(x-1)=(y-),即x=y-2,因为=(x,y),=(x-1,y),所以·=(x,y)·(x-1,y)=x2-x+y2=(y-2)2-y+2+y2=4y2-5y+6,令f(y)=4y2-5y+6,y∈.因为函数f(y)=4y2-5y+6在上单调递减,在上单调递增,所以f(y)min=4×-5×+6=.
所以·的最小值为,故选A.
【答案】 A
[强化训练]
1、解析:a·(a-2b)=a2-2a·b=2-2××2×=6.
答案:6
2、解析:=+=+,
=-=-+,
所以·=(4+3)·(4-3)=(162-92)=(16×62-9×42)=9.
答案:9
例2【解析】 (1)因为m+n=(2λ+3,3),m-n=(-1,-1),(m+n)⊥(m-n),
所以(m+n)·(m-n)=(2λ+3,3)·(-1,-1)=-2λ-6=0,解得λ=-3.
(2)设向量a与b的夹角为θ,因为a+b+c=0,
所以c=-(a+b),所以c2=(a+b)2,
即|c|2=|a|2+|b|2+2|a||b|cos θ,
所以19=4+9+12cos θ,
所以cos θ=,又0°≤θ≤180°,所以a与b的夹角为60°.
【答案】 (1)B (2)C
[强化训练]
1、解析:因为a=(1,0),b=(-1,m),所以ma-b=(m+1,-m).
由a⊥(ma-b)得a·(ma-b)=0,
即m+1=0,得m=-1.
答案:-1
2、解析:因为非零向量a,b满足a·(a-b)=0,所以a2=a·b,由|a-b|=|a|可得a2-2a·b+b2=a2,解得|b|=|a|,设a-b与b的夹角为θ,则cos θ====-,又0°≤θ≤180°,所以θ=135°.
答案:135°
例3【解析】 因为=(+)=(2a+2b+2a-6b)=2a-2b,所以||2=4(a-b)2=4(a2-2b·a+b2)=4×=4,则||=2.
【答案】 A
[强化训练]
1、解析:选D.因为a·(a-b)=8,
所以a·a-a·b=8,即|a|2-|a||b|cos〈a,b〉=8,
所以4+2|b|×=8,解得|b|=4.
【知识体系】
【难点突破】
难点突破一 平面向量数量积的运算
例1 如图,在平面四边形ABCD中,AB⊥BC,AD⊥CD,∠BAD=120°,AB=AD=1.若点E为边CD上的动点,则·的最小值为( )
A. B.
C. D.3
[方法技巧]
向量数量积的两种计算方法
(1)当已知向量的模和夹角θ时,可利用定义法求解,即a·b=|a||b|cos θ.
(2)当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.
[强化训练]
1、已知向量a,b的夹角为,|a|=,|b|=2,则a·(a-2b)=________.
2、设四边形ABCD为平行四边形,||=6,||=4,若点M,N满足=3,=2,则·等于________.
难点突破二 向量的夹角及垂直问题
例2 (1)已知向量m=(λ+1,1),n=(λ+2,2),若(m+n)⊥(m-n),则λ=( )
A.-4 B.-3
C.-2 D.-1
(2)已知a+b+c=0,|a|=2,|b|=3,|c|=,则向量a与b的夹角为( )
A.30° B.45°
C.60° D.以上都不对
[方法技巧]
解决两个向量垂直问题,其关键在于将问题转化为它们的数量积为零,与求夹角一样.若向量能用坐标表示(或能建立适当的直角坐标系),将它转化为“x1x2+y1y2=0”较为简单.
[强化训练]
1、设向量a=(1,0),b=(-1,m).若a⊥(ma-b),则m=________.
2、已知非零向量a,b满足|a-b|=|a|,a·(a-b)=0,则a-b与b夹角的大小为________.
难点突破三 向量的长度(模)与距离的问题
例3 已知平面向量a,b的夹角为,且|a|=,|b|=2,在△ABC中,=2a+2b,=2a-6b,D为BC的中点,则||等于( )
A.2 B.4
C.6 D.8
[方法技巧]
解决向量模的问题常用的策略
(1)应用公式:|a|=(其中a=(x,y)).
(2)应用三角形法则或平行四边形法则.
(3)应用向量不等式||a|-|b||≤|a±b|≤|a|+|b|.
(4)研究模的平方|a±b|2=(a±b)2.
[强化训练]
1、已知平面向量a,b的夹角为,且a·(a-b)=8,|a|=2,则|b|等于( )
A. B.2
C.3 D.4
参考答案
例1【解析】 以A为坐标原点,AB所在直线为x轴,建立如图的平面直角坐标系,
因为在平面四边形ABCD中,AB=AD=1,∠BAD=120°,所以A(0,0),B(1,0),D,设C(1,m),E(x,y),所以=,=,
因为AD⊥CD,所以·=0,即×+=0,解得m=,即C(1,),因为E在CD上,所以≤y≤,由∥,得(x-1)=(y-),即x=y-2,因为=(x,y),=(x-1,y),所以·=(x,y)·(x-1,y)=x2-x+y2=(y-2)2-y+2+y2=4y2-5y+6,令f(y)=4y2-5y+6,y∈.因为函数f(y)=4y2-5y+6在上单调递减,在上单调递增,所以f(y)min=4×-5×+6=.
所以·的最小值为,故选A.
【答案】 A
[强化训练]
1、解析:a·(a-2b)=a2-2a·b=2-2××2×=6.
答案:6
2、解析:=+=+,
=-=-+,
所以·=(4+3)·(4-3)=(162-92)=(16×62-9×42)=9.
答案:9
例2【解析】 (1)因为m+n=(2λ+3,3),m-n=(-1,-1),(m+n)⊥(m-n),
所以(m+n)·(m-n)=(2λ+3,3)·(-1,-1)=-2λ-6=0,解得λ=-3.
(2)设向量a与b的夹角为θ,因为a+b+c=0,
所以c=-(a+b),所以c2=(a+b)2,
即|c|2=|a|2+|b|2+2|a||b|cos θ,
所以19=4+9+12cos θ,
所以cos θ=,又0°≤θ≤180°,所以a与b的夹角为60°.
【答案】 (1)B (2)C
[强化训练]
1、解析:因为a=(1,0),b=(-1,m),所以ma-b=(m+1,-m).
由a⊥(ma-b)得a·(ma-b)=0,
即m+1=0,得m=-1.
答案:-1
2、解析:因为非零向量a,b满足a·(a-b)=0,所以a2=a·b,由|a-b|=|a|可得a2-2a·b+b2=a2,解得|b|=|a|,设a-b与b的夹角为θ,则cos θ====-,又0°≤θ≤180°,所以θ=135°.
答案:135°
例3【解析】 因为=(+)=(2a+2b+2a-6b)=2a-2b,所以||2=4(a-b)2=4(a2-2b·a+b2)=4×=4,则||=2.
【答案】 A
[强化训练]
1、解析:选D.因为a·(a-b)=8,
所以a·a-a·b=8,即|a|2-|a||b|cos〈a,b〉=8,
所以4+2|b|×=8,解得|b|=4.
