人教B版(2019)数学必修第三册综合复习:三角函数的图象和性质学案(含答案)
文档属性
| 名称 | 人教B版(2019)数学必修第三册综合复习:三角函数的图象和性质学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 103.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 21:06:04 | ||
图片预览




文档简介
三角函数的图象和性质
新课程标准 考向预测
1.能画出y=sin x,y=cos x,y=tan x的图象,了解三角函数的周期性. 2.借助图象理解正弦函数、余弦函数在[0,2π],正切函数在上的性质(如单调性、最大和最小值、图象与x轴交点等) . 命题角度 1.三角函数的定义域 2.三角函数的值域与最值 3.三角函数的单调性 4.三角函数的周期性、奇偶性、对称性
核心素养 直观想象、逻辑推理
【基础梳理】
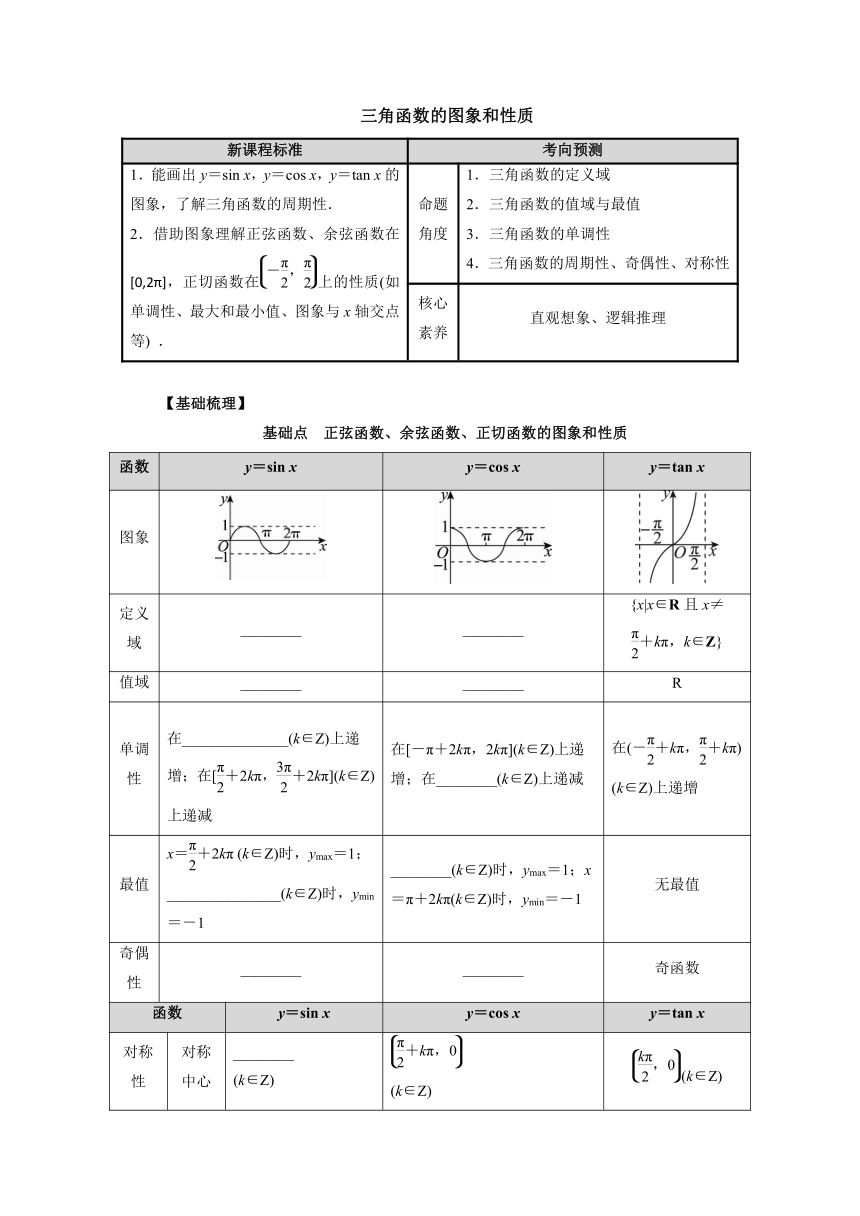
基础点 正弦函数、余弦函数、正切函数的图象和性质
函数 y=sin x y=cos x y=tan x
图象
定义域 ________ ________ {x|x∈R且x≠ +kπ,k∈Z}
值域 ________ ________ R
单调性 在______________(k∈Z)上递增;在[+2kπ,+2kπ](k∈Z)上递减 在[-π+2kπ,2kπ](k∈Z)上递增;在________(k∈Z)上递减 在(-+kπ,+kπ) (k∈Z)上递增
最值 x=+2kπ (k∈Z)时,ymax=1;_______________(k∈Z)时,ymin=-1 ________(k∈Z)时,ymax=1;x=π+2kπ(k∈Z)时,ymin=-1 无最值
奇偶性 ________ ________ 奇函数
函数 y=sin x y=cos x y=tan x
对称性 对称 中心 ________ (k∈Z) (k∈Z) (k∈Z)
对称 轴 直线x=+kπ (k∈Z) 直线________ (k∈Z) 无对称轴
最小正 周期 2π ________ π
基础小测
1.函数y=2-cos(x∈R)的最大值和最小正周期分别是( )
A.2,3π B.1,6π
C.3,6π D.3,3π
2.(2020届山西太原第五中学高三月考)下列函数中最小正周期为π,且图象关于直线x=对称的是( )
A.y=2sin(2x+) B.y=2sin(2x-)
C.y=2sin(+) D.y=2sin(2x-)
3.函数y=sin(x-)的图象的对称轴为__________________,对称中心为________________.
4.(2020届安徽阜阳临泉县第一中学高三月考)函数f(x)=cos x-sin x(x∈[0,π])的单调递增区间为________.
【考点突破】
考点一 三角函数的定义域(高考热度: ★★★)
[例1] 函数f(x)=-2tan(2x+)的定义域是( )
A.{x|x≠} B.{x|x≠-}
C.{x|x≠kπ+,k∈Z} D.{x|x≠+,k∈Z}
[例2] (2020届山东济宁一中高三月考)函数y=的定义域为_________________________.
方法总结
求三角函数的定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图象来求解.
考点二 三角函数的值域(或最值)(高考热度:★★★)
[例3] 函数f(x)=sin(x+)+cos(x-)的最大值为( )
A. B.1 C. D.
[例4] 函数f(x)=sin2x+cos x-(x∈(0,))的最大值是________.
方法总结
求三角函数的值域(或最值)的3种类型及解法思路
(1)形如y=asin x+bcos x+c的三角函数化为y=Asin(ωx+φ)+k的形式,再求值域(或最值);
(2)形如y=asin2x+bsin x+c的三角函数,可先设sin x=t,化为关于t的二次函数求值域(或最值);
(3)形如y=asin xcos x+b(sin x±cos x)+c的三角函数,可先设t=sin x±cos x,化为关于t的二次函数求值域(或最值).
考点微练
1.函数f(x)=3sin(2x-)在区间[0, ]上的值域为________.
2.(2020届江西新余四中高三月考)函数y=sin x-cos x+sin xcos x的值域为________________.
考点三 三角函数的单调性(高考热度:★★)
考向1 求三角函数的单调区间
[例5] 已知函数f(x)=sin2x-cos2x-2sin xcos x(x∈R).
(1)求f()的值;
(2)求f(x)的最小正周期及单调递增区间.
方法总结
求较为复杂的三角函数的单调区间时,首先化简成y=Asin(ωx+φ)的形式,再求y=Asin(ωx+φ)的单调区间,只需把ωx+φ看作一个整体代入y=sin x的相应单调区间内即可,注意要先把ω化为正数.
考点微练
1.(2020届天津耀华中学高三月考)已知函数f(x)=2sin(-2x),则函数f(x)的单调递减区间为( )
A.[+2kπ,+2kπ](k∈Z)
B.[-+2kπ,+2kπ](k∈Z)
C.[+kπ,+kπ](k∈Z)
D.[-+kπ,+kπ](k∈Z)
2.已知函数f(x)=sin+,ω>0,x∈R,且f(α)=-,f(β)=.若|α-β|的最小值为,则f=_____,函数f(x)的单调递增区间__________________________.
考向2 已知单调性求参数
[例6] 若f(x)=cos x-sin x在[-a,a]是减函数,则a的最大值是( )
A. B. C. D.π
方法总结
对于已知函数的单调区间的某一部分来确定参数ω的范围的问题,首先,明确已知的单调区间应为函数的单调区间的子集,其次,要确定已知函数的单调区间,从而利用它们之间的关系求解,另外,若是选择题,利用特值验证排除法求解更为简捷.
考点微练
(2020届福建闽侯第一中学高三月考)已知ω>0,函数f(x)=sin(ωx+)在(,π)上单调递减,则ω的取值范围是________.
对点变式
若已知ω>0,函数f(x)=cos(ωx+)在(,π)上单调递增,则ω的取值范围是________.
考点四 三角函数的周期性、奇偶性、图象的对称性(高考热度:★)
[例7] (多选题)已知函数f(x)=sin4x-cos4x,则下列说法正确的是( )
A.f(x)的最小正周期为π
B.f(x)的最大值为2
C.f(x)的图象关于y轴对称
D.f(x)在区间上单调递增
[例8] 已知函数f(x)=2sin(ωx+)(ω>0)的最小正周期为4π,则该函数的图象( )
A.关于点(,0)对称 B.关于点(,0)对称
C.关于直线x=对称 D.关于直线x=对称
考点微练
1.已知函数y=sin(2x+φ)(-<φ<)的图象关于直线x=对称,则φ的值为________.
2.已知函数f(x)=2sin(x+θ+),θ∈(-,)是偶函数,则θ的值为________.
3.若函数y=cos(ωx+)(ω∈N*)图象的一个对称中心是(,0),则ω的最小值为________.
方法总结
解决这类问题的关键是把原三角函数关系式统一角,统一名,即“一角一函数”,其解题思维流程是:
参考答案
基础小测
1.解析:由y=2-cos 知,ymax=2-(-1)=3,最小正周期T==6π.
2.解析:函数y=2sin的最小正周期T==π.∵sin=1,∴函数y=2sin的图象关于直线x=对称.
3.解析:由x-=+kπ,k∈Z,得x=+kπ,k∈Z;由x-=kπ,k∈Z,得x=+kπ,k∈Z,故函数y=sin的图象的对称轴为直线x=+kπ,k∈Z,对称中心为点,k∈Z.
4.解析:f(x)=cos x-sin x=cos .由2kπ-π≤x+≤2kπ(k∈Z),得2kπ-≤x≤2kπ-(k∈Z).∵x∈[0,π],∴f(x)在上单调递增.
【考点突破】
考点一 三角函数的定义域(高考热度: ★★★)
[例1] 解析:由正切函数的定义域,得2x+≠kπ+(k∈Z),即x≠+(k∈Z).故选D.
[例2] 解析:要使函数有意义,必须使sin x-cos x≥0.利用图象,在同一坐标系中画出[0,2π]上函数y=sin x和函数y=cos x的图象,如图所示.
在[0,2π]内,满足sin x=cos x的x为,,再结合正弦、余弦函数的周期性,所以原函数的定义域为{x.
考点二 三角函数的值域(或最值)(高考热度:★★★)
[例3] 解析:cos =cos =sin,则f(x)=sin+sin=sin,故函数的最大值为.
[例4] 解析:依题意知,f(x)=sin2x+cos x-=-cos2x+cos x+=-+1.因为x∈,所以cos x∈[0,1],因此当cos x=时,f(x)max=1.
考点微练
1.解析:当x∈时,2x-∈,∴sin∈,故3sin∈,∴函数f(x)在区间上的值域为.
2.解析:设t=sin x-cos x,则-≤t≤,t2=sin2x+cos2x-2sin xcos x,则sin xcos x=,∴y=-+t+=-(t-1)2+1.当t=1时,ymax=1;当t=-时,ymin=--.∴函数的值域为.
考点三 三角函数的单调性(高考热度:★★)
考向1 求三角函数的单调区间
[例5] 解:(1)由sin=,cos =-,
f =--2××,
得f =2.
(2)由cos 2x=cos2x-sin2x与sin 2x=2sin xcos x,
得f(x)=-cos 2x-sin 2x=-2sin,
所以f(x)的最小正周期是π.
由+2kπ≤2x+≤+2kπ(k∈Z),
解得+kπ≤x≤+kπ(k∈Z).
所以, f(x)的单调递增区间是(k∈Z).
考点微练
1.解析:函数的解析式可化为f(x)=-2sin.由2kπ-≤2x-≤2kπ+(k∈Z),得-+kπ≤x≤+kπ(k∈Z),即函数f(x)的单调递减区间为(k∈Z).
2.解析:函数f(x)=sin+,ω>0,x∈R,由f(α)=-,f(β)=,且|α-β|的最小值为,得=,即T=3π=,所以ω=.所以f(x)=sin+,则f=sin+=.由-+2kπ≤x-≤+2kπ,k∈Z,得-+3kπ≤x≤π+3kπ,k∈Z,即函数f(x)的单调递增区间为,k∈Z.
考向2 已知单调性求参数
[例6] 解析:f(x)=cos x-sin x=cos .
由题意得a>0,故-a+<.
因为f(x)=cos 在[-a,a]是减函数,
所以解得0考点微练
解析:由<x<π,ω>0,得+<ωx+<ωπ+.又y=sin x的单调递减区间为,k∈Z,所以k∈Z,解得4k+≤ω≤2k+,k∈Z.又由4k+-≤0,k∈Z且2k+>0,k∈Z,得k=0,所以ω∈.
对点变式
解析:函数y=cos x的单调递增区间为[-π+2kπ,2kπ],k∈Z,
则k∈Z,解得4k-≤ω≤2k-,k∈Z.
又由4k--≤0,k∈Z且2k->0,k∈Z,得k=1,所以ω∈.
考点四 三角函数的周期性、奇偶性、图象的对称性(高考热度:★)
[例7] 解析:∵f(x)=sin4x-cos4x=sin2x-cos2x=-cos 2x,∴函数f(x)的最小正周期T=π,f(x)的最大值为1.∵f(-x)=-cos(-2x)=-cos 2x=f(x),∴f(x)为偶函数,其图象关于y轴对称.∵y=cos 2x在上单调递减,∴f(x)=-cos 2x在上单调递增.故选ACD.
[例8] 解析:因为函数f(x)=2sin(ω>0)的最小正周期为4π,而T==4π,所以ω=,即f(x)=2sin.令+=+kπ(k∈Z),解得x=+2kπ(k∈Z),故f(x)的对称轴为直线x=+2kπ(k∈Z).令+=kπ(k∈Z),
解得x=-+2kπ(k∈Z),故f(x)的对称中心为点(k∈Z),对比选项可知B正确.
考点微练
1.解析:由题意得f=sin=±1,∴+φ=kπ+(k∈Z),∴φ=kπ-(k∈Z).∵φ∈,∴φ=-.
2.解析:∵函数f(x)为偶函数,∴θ+=kπ+(k∈Z).又θ∈,∴θ+=,解得θ=,经检验符合题意.
3.解析:由题意知+=kπ+(k∈Z),∴ω=6k+2(k∈Z).又ω∈N*,∴ωmin=2.
新课程标准 考向预测
1.能画出y=sin x,y=cos x,y=tan x的图象,了解三角函数的周期性. 2.借助图象理解正弦函数、余弦函数在[0,2π],正切函数在上的性质(如单调性、最大和最小值、图象与x轴交点等) . 命题角度 1.三角函数的定义域 2.三角函数的值域与最值 3.三角函数的单调性 4.三角函数的周期性、奇偶性、对称性
核心素养 直观想象、逻辑推理
【基础梳理】
基础点 正弦函数、余弦函数、正切函数的图象和性质
函数 y=sin x y=cos x y=tan x
图象
定义域 ________ ________ {x|x∈R且x≠ +kπ,k∈Z}
值域 ________ ________ R
单调性 在______________(k∈Z)上递增;在[+2kπ,+2kπ](k∈Z)上递减 在[-π+2kπ,2kπ](k∈Z)上递增;在________(k∈Z)上递减 在(-+kπ,+kπ) (k∈Z)上递增
最值 x=+2kπ (k∈Z)时,ymax=1;_______________(k∈Z)时,ymin=-1 ________(k∈Z)时,ymax=1;x=π+2kπ(k∈Z)时,ymin=-1 无最值
奇偶性 ________ ________ 奇函数
函数 y=sin x y=cos x y=tan x
对称性 对称 中心 ________ (k∈Z) (k∈Z) (k∈Z)
对称 轴 直线x=+kπ (k∈Z) 直线________ (k∈Z) 无对称轴
最小正 周期 2π ________ π
基础小测
1.函数y=2-cos(x∈R)的最大值和最小正周期分别是( )
A.2,3π B.1,6π
C.3,6π D.3,3π
2.(2020届山西太原第五中学高三月考)下列函数中最小正周期为π,且图象关于直线x=对称的是( )
A.y=2sin(2x+) B.y=2sin(2x-)
C.y=2sin(+) D.y=2sin(2x-)
3.函数y=sin(x-)的图象的对称轴为__________________,对称中心为________________.
4.(2020届安徽阜阳临泉县第一中学高三月考)函数f(x)=cos x-sin x(x∈[0,π])的单调递增区间为________.
【考点突破】
考点一 三角函数的定义域(高考热度: ★★★)
[例1] 函数f(x)=-2tan(2x+)的定义域是( )
A.{x|x≠} B.{x|x≠-}
C.{x|x≠kπ+,k∈Z} D.{x|x≠+,k∈Z}
[例2] (2020届山东济宁一中高三月考)函数y=的定义域为_________________________.
方法总结
求三角函数的定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图象来求解.
考点二 三角函数的值域(或最值)(高考热度:★★★)
[例3] 函数f(x)=sin(x+)+cos(x-)的最大值为( )
A. B.1 C. D.
[例4] 函数f(x)=sin2x+cos x-(x∈(0,))的最大值是________.
方法总结
求三角函数的值域(或最值)的3种类型及解法思路
(1)形如y=asin x+bcos x+c的三角函数化为y=Asin(ωx+φ)+k的形式,再求值域(或最值);
(2)形如y=asin2x+bsin x+c的三角函数,可先设sin x=t,化为关于t的二次函数求值域(或最值);
(3)形如y=asin xcos x+b(sin x±cos x)+c的三角函数,可先设t=sin x±cos x,化为关于t的二次函数求值域(或最值).
考点微练
1.函数f(x)=3sin(2x-)在区间[0, ]上的值域为________.
2.(2020届江西新余四中高三月考)函数y=sin x-cos x+sin xcos x的值域为________________.
考点三 三角函数的单调性(高考热度:★★)
考向1 求三角函数的单调区间
[例5] 已知函数f(x)=sin2x-cos2x-2sin xcos x(x∈R).
(1)求f()的值;
(2)求f(x)的最小正周期及单调递增区间.
方法总结
求较为复杂的三角函数的单调区间时,首先化简成y=Asin(ωx+φ)的形式,再求y=Asin(ωx+φ)的单调区间,只需把ωx+φ看作一个整体代入y=sin x的相应单调区间内即可,注意要先把ω化为正数.
考点微练
1.(2020届天津耀华中学高三月考)已知函数f(x)=2sin(-2x),则函数f(x)的单调递减区间为( )
A.[+2kπ,+2kπ](k∈Z)
B.[-+2kπ,+2kπ](k∈Z)
C.[+kπ,+kπ](k∈Z)
D.[-+kπ,+kπ](k∈Z)
2.已知函数f(x)=sin+,ω>0,x∈R,且f(α)=-,f(β)=.若|α-β|的最小值为,则f=_____,函数f(x)的单调递增区间__________________________.
考向2 已知单调性求参数
[例6] 若f(x)=cos x-sin x在[-a,a]是减函数,则a的最大值是( )
A. B. C. D.π
方法总结
对于已知函数的单调区间的某一部分来确定参数ω的范围的问题,首先,明确已知的单调区间应为函数的单调区间的子集,其次,要确定已知函数的单调区间,从而利用它们之间的关系求解,另外,若是选择题,利用特值验证排除法求解更为简捷.
考点微练
(2020届福建闽侯第一中学高三月考)已知ω>0,函数f(x)=sin(ωx+)在(,π)上单调递减,则ω的取值范围是________.
对点变式
若已知ω>0,函数f(x)=cos(ωx+)在(,π)上单调递增,则ω的取值范围是________.
考点四 三角函数的周期性、奇偶性、图象的对称性(高考热度:★)
[例7] (多选题)已知函数f(x)=sin4x-cos4x,则下列说法正确的是( )
A.f(x)的最小正周期为π
B.f(x)的最大值为2
C.f(x)的图象关于y轴对称
D.f(x)在区间上单调递增
[例8] 已知函数f(x)=2sin(ωx+)(ω>0)的最小正周期为4π,则该函数的图象( )
A.关于点(,0)对称 B.关于点(,0)对称
C.关于直线x=对称 D.关于直线x=对称
考点微练
1.已知函数y=sin(2x+φ)(-<φ<)的图象关于直线x=对称,则φ的值为________.
2.已知函数f(x)=2sin(x+θ+),θ∈(-,)是偶函数,则θ的值为________.
3.若函数y=cos(ωx+)(ω∈N*)图象的一个对称中心是(,0),则ω的最小值为________.
方法总结
解决这类问题的关键是把原三角函数关系式统一角,统一名,即“一角一函数”,其解题思维流程是:
参考答案
基础小测
1.解析:由y=2-cos 知,ymax=2-(-1)=3,最小正周期T==6π.
2.解析:函数y=2sin的最小正周期T==π.∵sin=1,∴函数y=2sin的图象关于直线x=对称.
3.解析:由x-=+kπ,k∈Z,得x=+kπ,k∈Z;由x-=kπ,k∈Z,得x=+kπ,k∈Z,故函数y=sin的图象的对称轴为直线x=+kπ,k∈Z,对称中心为点,k∈Z.
4.解析:f(x)=cos x-sin x=cos .由2kπ-π≤x+≤2kπ(k∈Z),得2kπ-≤x≤2kπ-(k∈Z).∵x∈[0,π],∴f(x)在上单调递增.
【考点突破】
考点一 三角函数的定义域(高考热度: ★★★)
[例1] 解析:由正切函数的定义域,得2x+≠kπ+(k∈Z),即x≠+(k∈Z).故选D.
[例2] 解析:要使函数有意义,必须使sin x-cos x≥0.利用图象,在同一坐标系中画出[0,2π]上函数y=sin x和函数y=cos x的图象,如图所示.
在[0,2π]内,满足sin x=cos x的x为,,再结合正弦、余弦函数的周期性,所以原函数的定义域为{x.
考点二 三角函数的值域(或最值)(高考热度:★★★)
[例3] 解析:cos =cos =sin,则f(x)=sin+sin=sin,故函数的最大值为.
[例4] 解析:依题意知,f(x)=sin2x+cos x-=-cos2x+cos x+=-+1.因为x∈,所以cos x∈[0,1],因此当cos x=时,f(x)max=1.
考点微练
1.解析:当x∈时,2x-∈,∴sin∈,故3sin∈,∴函数f(x)在区间上的值域为.
2.解析:设t=sin x-cos x,则-≤t≤,t2=sin2x+cos2x-2sin xcos x,则sin xcos x=,∴y=-+t+=-(t-1)2+1.当t=1时,ymax=1;当t=-时,ymin=--.∴函数的值域为.
考点三 三角函数的单调性(高考热度:★★)
考向1 求三角函数的单调区间
[例5] 解:(1)由sin=,cos =-,
f =--2××,
得f =2.
(2)由cos 2x=cos2x-sin2x与sin 2x=2sin xcos x,
得f(x)=-cos 2x-sin 2x=-2sin,
所以f(x)的最小正周期是π.
由+2kπ≤2x+≤+2kπ(k∈Z),
解得+kπ≤x≤+kπ(k∈Z).
所以, f(x)的单调递增区间是(k∈Z).
考点微练
1.解析:函数的解析式可化为f(x)=-2sin.由2kπ-≤2x-≤2kπ+(k∈Z),得-+kπ≤x≤+kπ(k∈Z),即函数f(x)的单调递减区间为(k∈Z).
2.解析:函数f(x)=sin+,ω>0,x∈R,由f(α)=-,f(β)=,且|α-β|的最小值为,得=,即T=3π=,所以ω=.所以f(x)=sin+,则f=sin+=.由-+2kπ≤x-≤+2kπ,k∈Z,得-+3kπ≤x≤π+3kπ,k∈Z,即函数f(x)的单调递增区间为,k∈Z.
考向2 已知单调性求参数
[例6] 解析:f(x)=cos x-sin x=cos .
由题意得a>0,故-a+<.
因为f(x)=cos 在[-a,a]是减函数,
所以解得0
解析:由<x<π,ω>0,得+<ωx+<ωπ+.又y=sin x的单调递减区间为,k∈Z,所以k∈Z,解得4k+≤ω≤2k+,k∈Z.又由4k+-≤0,k∈Z且2k+>0,k∈Z,得k=0,所以ω∈.
对点变式
解析:函数y=cos x的单调递增区间为[-π+2kπ,2kπ],k∈Z,
则k∈Z,解得4k-≤ω≤2k-,k∈Z.
又由4k--≤0,k∈Z且2k->0,k∈Z,得k=1,所以ω∈.
考点四 三角函数的周期性、奇偶性、图象的对称性(高考热度:★)
[例7] 解析:∵f(x)=sin4x-cos4x=sin2x-cos2x=-cos 2x,∴函数f(x)的最小正周期T=π,f(x)的最大值为1.∵f(-x)=-cos(-2x)=-cos 2x=f(x),∴f(x)为偶函数,其图象关于y轴对称.∵y=cos 2x在上单调递减,∴f(x)=-cos 2x在上单调递增.故选ACD.
[例8] 解析:因为函数f(x)=2sin(ω>0)的最小正周期为4π,而T==4π,所以ω=,即f(x)=2sin.令+=+kπ(k∈Z),解得x=+2kπ(k∈Z),故f(x)的对称轴为直线x=+2kπ(k∈Z).令+=kπ(k∈Z),
解得x=-+2kπ(k∈Z),故f(x)的对称中心为点(k∈Z),对比选项可知B正确.
考点微练
1.解析:由题意得f=sin=±1,∴+φ=kπ+(k∈Z),∴φ=kπ-(k∈Z).∵φ∈,∴φ=-.
2.解析:∵函数f(x)为偶函数,∴θ+=kπ+(k∈Z).又θ∈,∴θ+=,解得θ=,经检验符合题意.
3.解析:由题意知+=kπ+(k∈Z),∴ω=6k+2(k∈Z).又ω∈N*,∴ωmin=2.
