人教B版(2019)数学必修第三册综合复习:同角三角函数的基本关系及诱导公式学案(含答案)
文档属性
| 名称 | 人教B版(2019)数学必修第三册综合复习:同角三角函数的基本关系及诱导公式学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 45.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 21:07:32 | ||
图片预览


文档简介
同角三角函数的基本关系及诱导公式
新课程标准 考向预测
1.理解同角三角函数的基本关系式:sin2x+cos2x=1,=tan x. 2.借助单位圆中的三角函数线推导出诱导公式. 命题角度 1.同角三角函数基本关系式的应用 2.诱导公式的应用 3.同角三角函数基本关系式与诱导公式的活用
核心 素养 数学运算
【基础梳理】
基础点一 同角三角函数的基本关系
1.平方关系:①_______________________.
2.商数关系:② ______________________.
注意:平方关系对任意角都成立,而商数关系中α≠kπ+(k∈Z).
基础小测
1.(2020届山西太原第五中学高三月考)已知α为锐角,且sin α=,则cos α=( )
A.- B. C.- D.
2.(2020届山东曲阜二中高三月考)设tan α=,π<α<,则sin α-cos α的值为( )
A.-+ B.--
C.+ D.-
3.(2020届湖北荆州中学高三月考)已知直线2x-y-1=0的倾斜角为α,则sin 2α-2cos2α=( )
A. B.-
C.- D.-
基础点二 诱导公式
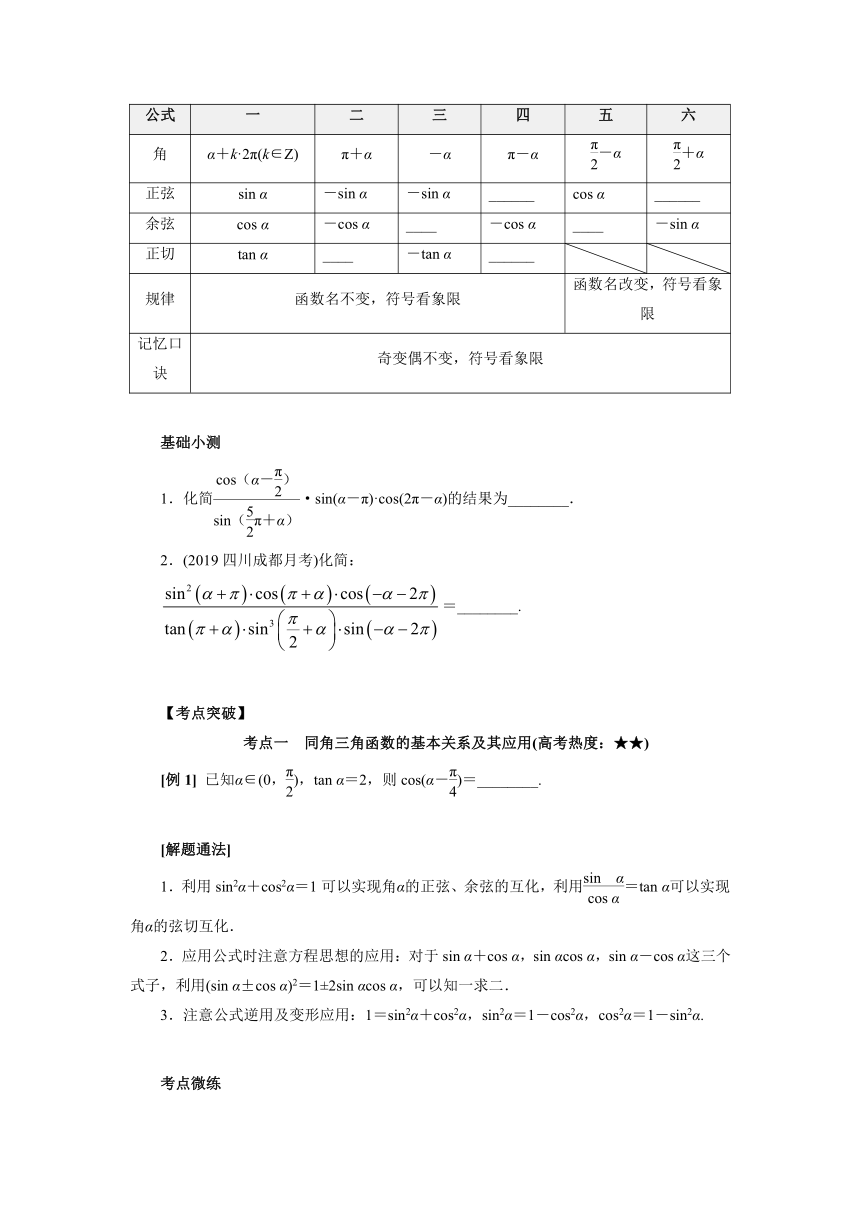
公式 一 二 三 四 五 六
角 α+k·2π(k∈Z) π+α -α π-α -α +α
正弦 sin α -sin α -sin α ______ cos α ______
余弦 cos α -cos α ____ -cos α ____ -sin α
正切 tan α ____ -tan α ______
规律 函数名不变,符号看象限 函数名改变,符号看象限
记忆口诀 奇变偶不变,符号看象限
基础小测
1.化简·sin(α-π)·cos(2π-α)的结果为________.
2.(2019四川成都月考)化简:
=________.
【考点突破】
考点一 同角三角函数的基本关系及其应用(高考热度:★★)
[例1] 已知α∈(0,),tan α=2,则cos(α-)=________.
[解题通法]
1.利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用=tan α可以实现角α的弦切互化.
2.应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.
3.注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.
考点微练
1.已知α是第四象限角,sin α=-,则tan α等于( )
A.- B. C.- D.
2.已知sin αcos α=,且<α<,则cos α-sin α的值为( )
A.- B.
C.- D.
3.(2019广东惠阳高级中学月考)已知α∈(,π),4sin α+3cos α=0,则sin 2α+3cos2α的值为________.
4.在平面直角坐标系xOy中,角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边交单位圆O于点P(a,b),且a+b=,则ab=________,cos=________.
考点二 诱导公式的应用(高考热度:★★)
[例2] 在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sin α=,则sin β=________.
[方法总结]
1.诱导公式的两个应用
(1)求值:负化正,大化小,化到锐角为终了.
(2)化简:统一角,统一名,同角名少为终了.
2.含2π整数倍的诱导公式的应用
由终边相同的角的关系可知,在计算含有2π的整
数倍的三角函数式中,可直接将2π的整数倍去掉后再进行运算.
考点微练
1.若cos(-α)=,则cos(π-2α)=( )
A. B. C.- D.-
2.设f(α)= (1+2sin α≠0),则f()=________.
考点三 同角三角函数基本关系式与诱导公式的综合运用(高考热度:★)
[例3] 已知θ是第四象限角,且sin(θ+)=,则tan(θ-)=________.
[易错提示]
注意θ+与-θ互余.
[方法总结]
1.利用同角三角函数关系式和诱导公式求值或化简时,关键是寻求条件、结论间的联系,灵活运用公式进行变形.常见的互余的角:-α与+α;+α与-α;+α与-α等.常见的互补的角:+θ与-θ;+θ与-θ等.
2.注意角的范围对三角函数符号的影响.
考点微练
1.(2020届江西九江第一中学高三月考)已知α为锐角,且2tan(π-α)-3cos(+β)+5=0,tan(π+α)+6sin(π+β)-1=0,则sin α的值是( )
A. B. C. D.
2.已知α∈(0,π),且cos α=-,则sin(-α)·tan α=( )
A.- B.- C. D.
3.已知-π<x<0,sin(π+x)-cos x=-.
(1)求sin x-cos x的值;
(2)求的值.
参考答案
【基础梳理】
基础点一 同角三角函数的基本关系
基础小测
1.解析:因为α为锐角,所以cos α==.故选B.
2.解析:∵ tan α=,π<α<,∴sin α=-,cos α=-,∴sin α-cos α=--=-.故选A.
3.解析:由题意知tan α=2,∴sin 2α-2cos2α===.故选A.
基础点二 诱导公式
基础小测
1.解析:原式=·(-sin α)·cos α=-sin2α.
2.解析:原式===1.
【考点突破】
考点一 同角三角函数的基本关系及其应用(高考热度:★★)
[例1] 解析:因为α∈,且tan α==2,所以sin α=2cos α.又sin2α+cos2α=1,所以sin α=,cos α=.所以cos =cos αcos +sin αsin=×+×=.
考点微练
1.解析:因为α是第四象限角,sin α=-,所以cos α==,故tan α==-.
2.解析:∵<α<,∴cos α<0,sin α<0且cos α>sin α,∴cos α-sin α>0.又(cos α-sin α)2=1-2sin αcos α=1-2×=,∴cos α-sin α=.
3.解析:由4sin α+3cos α=0,可得tan α=-,则sin 2α+3cos2α====.
4.解析:由题知sin α=b,cos α=a.∵a+b=,∴sin α+cos α=.两边平方可得sin2α+cos2α+2sin αcos α=,∴1+2sin αcos α=,∴2sin αcos α=.∴sin αcos α=ab=,∴cos=-sin 2α=-2sinαcos α=-.
考点二 诱导公式的应用(高考热度:★★)
[例2] 解析:α与β的终边关于y轴对称,则α+β=π+2kπ,k∈Z,
∴β=π-α+2kπ,k∈Z.∴sin β=sin(π-α+2kπ)=sin α=.
考点微练
1.解析:由cos =,得sin α=.
∴cos (π-2α)=-cos 2α=-(1-2sin2α)=2sin2α-1=2×-1=-.
2.解析:∵f(α)====,∴f===.
考点三 同角三角函数基本关系式与诱导公式的综合运用(高考热度:★)
[例3] 解析:由题意,得cos =,∴tan=.
∴tan=tan=-=-.
考点微练
1.解析:由已知可得-2tan α+3sin β+5=0,tan α-6sin β-1=0,解得tan α=3.又α为锐角,sin2α+cos2α=1,故sin α=.
2.解析:∵α∈(0,π),且cos α=-,∴sin α=,因此sin·tan α=cos α·=sin α=.
3.解析:(1)由已知,得sin x+cos x=,两边平方得sin2x+2sin xcos x+cos2x=,整理得2sin xcos x=-.∵(sin x-cos x)2=1-2sin xcos x=,由-π<x<0知,sin x<0,又sin xcos x=-<0,∴cos x>0,∴sin x-cos x<0,故sin x-cos x=-.
(2) ====-.
新课程标准 考向预测
1.理解同角三角函数的基本关系式:sin2x+cos2x=1,=tan x. 2.借助单位圆中的三角函数线推导出诱导公式. 命题角度 1.同角三角函数基本关系式的应用 2.诱导公式的应用 3.同角三角函数基本关系式与诱导公式的活用
核心 素养 数学运算
【基础梳理】
基础点一 同角三角函数的基本关系
1.平方关系:①_______________________.
2.商数关系:② ______________________.
注意:平方关系对任意角都成立,而商数关系中α≠kπ+(k∈Z).
基础小测
1.(2020届山西太原第五中学高三月考)已知α为锐角,且sin α=,则cos α=( )
A.- B. C.- D.
2.(2020届山东曲阜二中高三月考)设tan α=,π<α<,则sin α-cos α的值为( )
A.-+ B.--
C.+ D.-
3.(2020届湖北荆州中学高三月考)已知直线2x-y-1=0的倾斜角为α,则sin 2α-2cos2α=( )
A. B.-
C.- D.-
基础点二 诱导公式
公式 一 二 三 四 五 六
角 α+k·2π(k∈Z) π+α -α π-α -α +α
正弦 sin α -sin α -sin α ______ cos α ______
余弦 cos α -cos α ____ -cos α ____ -sin α
正切 tan α ____ -tan α ______
规律 函数名不变,符号看象限 函数名改变,符号看象限
记忆口诀 奇变偶不变,符号看象限
基础小测
1.化简·sin(α-π)·cos(2π-α)的结果为________.
2.(2019四川成都月考)化简:
=________.
【考点突破】
考点一 同角三角函数的基本关系及其应用(高考热度:★★)
[例1] 已知α∈(0,),tan α=2,则cos(α-)=________.
[解题通法]
1.利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用=tan α可以实现角α的弦切互化.
2.应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.
3.注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.
考点微练
1.已知α是第四象限角,sin α=-,则tan α等于( )
A.- B. C.- D.
2.已知sin αcos α=,且<α<,则cos α-sin α的值为( )
A.- B.
C.- D.
3.(2019广东惠阳高级中学月考)已知α∈(,π),4sin α+3cos α=0,则sin 2α+3cos2α的值为________.
4.在平面直角坐标系xOy中,角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边交单位圆O于点P(a,b),且a+b=,则ab=________,cos=________.
考点二 诱导公式的应用(高考热度:★★)
[例2] 在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sin α=,则sin β=________.
[方法总结]
1.诱导公式的两个应用
(1)求值:负化正,大化小,化到锐角为终了.
(2)化简:统一角,统一名,同角名少为终了.
2.含2π整数倍的诱导公式的应用
由终边相同的角的关系可知,在计算含有2π的整
数倍的三角函数式中,可直接将2π的整数倍去掉后再进行运算.
考点微练
1.若cos(-α)=,则cos(π-2α)=( )
A. B. C.- D.-
2.设f(α)= (1+2sin α≠0),则f()=________.
考点三 同角三角函数基本关系式与诱导公式的综合运用(高考热度:★)
[例3] 已知θ是第四象限角,且sin(θ+)=,则tan(θ-)=________.
[易错提示]
注意θ+与-θ互余.
[方法总结]
1.利用同角三角函数关系式和诱导公式求值或化简时,关键是寻求条件、结论间的联系,灵活运用公式进行变形.常见的互余的角:-α与+α;+α与-α;+α与-α等.常见的互补的角:+θ与-θ;+θ与-θ等.
2.注意角的范围对三角函数符号的影响.
考点微练
1.(2020届江西九江第一中学高三月考)已知α为锐角,且2tan(π-α)-3cos(+β)+5=0,tan(π+α)+6sin(π+β)-1=0,则sin α的值是( )
A. B. C. D.
2.已知α∈(0,π),且cos α=-,则sin(-α)·tan α=( )
A.- B.- C. D.
3.已知-π<x<0,sin(π+x)-cos x=-.
(1)求sin x-cos x的值;
(2)求的值.
参考答案
【基础梳理】
基础点一 同角三角函数的基本关系
基础小测
1.解析:因为α为锐角,所以cos α==.故选B.
2.解析:∵ tan α=,π<α<,∴sin α=-,cos α=-,∴sin α-cos α=--=-.故选A.
3.解析:由题意知tan α=2,∴sin 2α-2cos2α===.故选A.
基础点二 诱导公式
基础小测
1.解析:原式=·(-sin α)·cos α=-sin2α.
2.解析:原式===1.
【考点突破】
考点一 同角三角函数的基本关系及其应用(高考热度:★★)
[例1] 解析:因为α∈,且tan α==2,所以sin α=2cos α.又sin2α+cos2α=1,所以sin α=,cos α=.所以cos =cos αcos +sin αsin=×+×=.
考点微练
1.解析:因为α是第四象限角,sin α=-,所以cos α==,故tan α==-.
2.解析:∵<α<,∴cos α<0,sin α<0且cos α>sin α,∴cos α-sin α>0.又(cos α-sin α)2=1-2sin αcos α=1-2×=,∴cos α-sin α=.
3.解析:由4sin α+3cos α=0,可得tan α=-,则sin 2α+3cos2α====.
4.解析:由题知sin α=b,cos α=a.∵a+b=,∴sin α+cos α=.两边平方可得sin2α+cos2α+2sin αcos α=,∴1+2sin αcos α=,∴2sin αcos α=.∴sin αcos α=ab=,∴cos=-sin 2α=-2sinαcos α=-.
考点二 诱导公式的应用(高考热度:★★)
[例2] 解析:α与β的终边关于y轴对称,则α+β=π+2kπ,k∈Z,
∴β=π-α+2kπ,k∈Z.∴sin β=sin(π-α+2kπ)=sin α=.
考点微练
1.解析:由cos =,得sin α=.
∴cos (π-2α)=-cos 2α=-(1-2sin2α)=2sin2α-1=2×-1=-.
2.解析:∵f(α)====,∴f===.
考点三 同角三角函数基本关系式与诱导公式的综合运用(高考热度:★)
[例3] 解析:由题意,得cos =,∴tan=.
∴tan=tan=-=-.
考点微练
1.解析:由已知可得-2tan α+3sin β+5=0,tan α-6sin β-1=0,解得tan α=3.又α为锐角,sin2α+cos2α=1,故sin α=.
2.解析:∵α∈(0,π),且cos α=-,∴sin α=,因此sin·tan α=cos α·=sin α=.
3.解析:(1)由已知,得sin x+cos x=,两边平方得sin2x+2sin xcos x+cos2x=,整理得2sin xcos x=-.∵(sin x-cos x)2=1-2sin xcos x=,由-π<x<0知,sin x<0,又sin xcos x=-<0,∴cos x>0,∴sin x-cos x<0,故sin x-cos x=-.
(2) ====-.
