23.2.2 中心对称图形 课件(共21张PPT)
文档属性
| 名称 | 23.2.2 中心对称图形 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 13:22:49 | ||
图片预览







文档简介
(共21张PPT)
第二十三章 旋 转
23.2.2 中心对称图形
23.2 中心对称
学习目标
1.会识别中心对称图形. (难点)
2.会运用中心对称图形的性质解决实际问题.
(重点)
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
我们上节课学习了中心对称的相关知识,中心对称是指两个图形的关系,而把这两个图形看作一个整体是什么图形呢?是我们这节课所要学习的中心对称图形.
讲授新知
贰
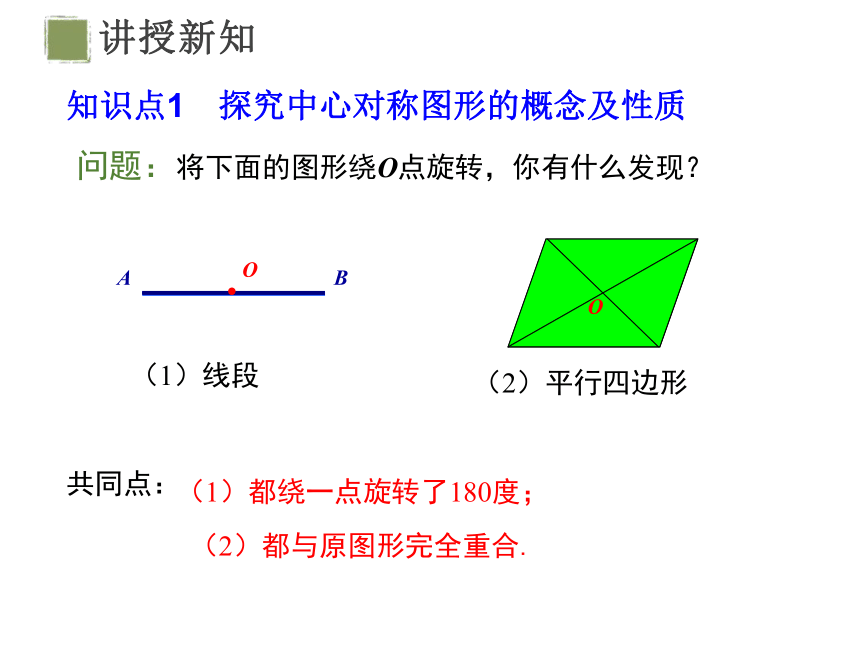
(1)线段
(2)平行四边形
A
B
问题:将下面的图形绕O点旋转,你有什么发现?
O
O
共同点:
(1)都绕一点旋转了180度;
(2)都与原图形完全重合.
知识点1 探究中心对称图形的概念及性质
讲授新知
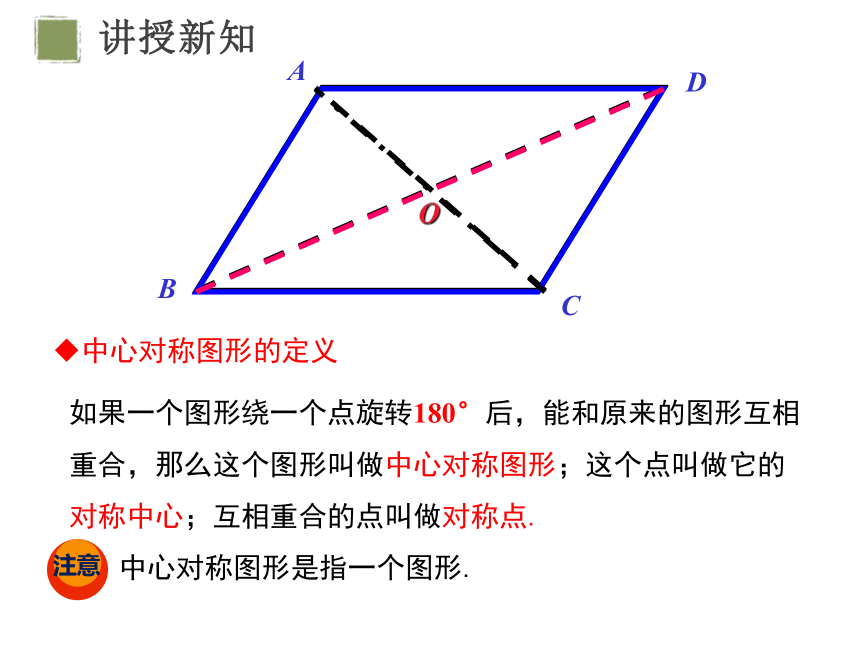
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
O
B
A
C
D
中心对称图形的定义
中心对称图形是指一个图形.
注意
讲授新知
中心对称与中心对称图形的区别与联系
中心对称 中心对称图形
区别 (1) 是针对两个图形而言的 (2) 是指两个图形的(位置)关系 (3) 对称点在两个图形上 (4) 对称中心可能在两个图形的外部,也可能在图形的内部或图形上 (1) 是针对一个图形而言的
(2) 是指具有某种性质的一个图形
(3) 对称点在一个图形上
(4) 对称中心在图形内部
联系 (1) 都是根据把图形旋转180°后能重合定义的. (2) 两者可以相互转化,若把成中心对称的两个图形视为一个整体,则整个图形是中心对称图形;若把一个中心对称图形相互对称的两部分看作两个图形,则这两个图形成中心对称. 讲授新知
例1(1)选取1个涂上阴影,使4个阴影小正
方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取1个涂上阴影,使4个阴影小正方形组成一个既是轴对称图形,又是中心对称图形.
范例应用
知识点2 中心对称图形的性质
讲授新知
(1)中心对称图形上对称点的连线必经过对称中心,且被对称中心平分,即过对称中心的直线与中心对称图形所交的两个对应交点是对称点.
(2)过对称中心的直线把中心对称图形分成全等的两部分(即周长和面积分别相等).
例2 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为_______.
解析:由于矩形是中心对称图形,所以依题意可知△BOF与△DOE关于点O成中心对称,由此图中阴影部分的三个三角形就可以转化到直角△ADC中,易得阴影部分的面积为3.
3
范例应用
例3 请你用无刻度的直尺画一条直线把他们分成面积相等的两部分,你怎样画?
割法1
范例应用
割法2
当堂训练
叁
当堂训练
1.下面图形中,是中心对称图形的是( )
2.下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
3.有4张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转180°后得到的图形如图(2)所示,那么她所旋转的牌从左起是( )
A.第一张或第二张 B.第二张或第三张
C.第三张或第四张 D.第一张或第四张
C
D
A
课堂小结
肆
课堂小结
中心对称图形
定义
性质
应用
绕着内部一点旋转180°能与本身重合的图形
经过对称中心的直线把原图形分成面积相等的两部分
美丽的中心对称图形在建筑物和工艺品等领域非常常见
课后作业
基础题:1.课后练习 P70第 2,8题。
提高题:2.学有余力的学生把练习册的提高题部分做了
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二十三章 旋 转
23.2.2 中心对称图形
23.2 中心对称
学习目标
1.会识别中心对称图形. (难点)
2.会运用中心对称图形的性质解决实际问题.
(重点)
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
我们上节课学习了中心对称的相关知识,中心对称是指两个图形的关系,而把这两个图形看作一个整体是什么图形呢?是我们这节课所要学习的中心对称图形.
讲授新知
贰
(1)线段
(2)平行四边形
A
B
问题:将下面的图形绕O点旋转,你有什么发现?
O
O
共同点:
(1)都绕一点旋转了180度;
(2)都与原图形完全重合.
知识点1 探究中心对称图形的概念及性质
讲授新知
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
O
B
A
C
D
中心对称图形的定义
中心对称图形是指一个图形.
注意
讲授新知
中心对称与中心对称图形的区别与联系
中心对称 中心对称图形
区别 (1) 是针对两个图形而言的 (2) 是指两个图形的(位置)关系 (3) 对称点在两个图形上 (4) 对称中心可能在两个图形的外部,也可能在图形的内部或图形上 (1) 是针对一个图形而言的
(2) 是指具有某种性质的一个图形
(3) 对称点在一个图形上
(4) 对称中心在图形内部
联系 (1) 都是根据把图形旋转180°后能重合定义的. (2) 两者可以相互转化,若把成中心对称的两个图形视为一个整体,则整个图形是中心对称图形;若把一个中心对称图形相互对称的两部分看作两个图形,则这两个图形成中心对称. 讲授新知
例1(1)选取1个涂上阴影,使4个阴影小正
方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取1个涂上阴影,使4个阴影小正方形组成一个既是轴对称图形,又是中心对称图形.
范例应用
知识点2 中心对称图形的性质
讲授新知
(1)中心对称图形上对称点的连线必经过对称中心,且被对称中心平分,即过对称中心的直线与中心对称图形所交的两个对应交点是对称点.
(2)过对称中心的直线把中心对称图形分成全等的两部分(即周长和面积分别相等).
例2 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为_______.
解析:由于矩形是中心对称图形,所以依题意可知△BOF与△DOE关于点O成中心对称,由此图中阴影部分的三个三角形就可以转化到直角△ADC中,易得阴影部分的面积为3.
3
范例应用
例3 请你用无刻度的直尺画一条直线把他们分成面积相等的两部分,你怎样画?
割法1
范例应用
割法2
当堂训练
叁
当堂训练
1.下面图形中,是中心对称图形的是( )
2.下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
3.有4张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转180°后得到的图形如图(2)所示,那么她所旋转的牌从左起是( )
A.第一张或第二张 B.第二张或第三张
C.第三张或第四张 D.第一张或第四张
C
D
A
课堂小结
肆
课堂小结
中心对称图形
定义
性质
应用
绕着内部一点旋转180°能与本身重合的图形
经过对称中心的直线把原图形分成面积相等的两部分
美丽的中心对称图形在建筑物和工艺品等领域非常常见
课后作业
基础题:1.课后练习 P70第 2,8题。
提高题:2.学有余力的学生把练习册的提高题部分做了
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
