23.2.3 关于原点对称的点的坐标 课件(共21张PPT)
文档属性
| 名称 | 23.2.3 关于原点对称的点的坐标 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 13:24:35 | ||
图片预览








文档简介
(共21张PPT)
第二十三章 旋 转
23.2.3 关于原点对称的点的坐标
23.2 中心对称
学习目标
1.掌握两点关于原点对称时,横纵坐标的关系.(难点)
2.会在平面直角坐标系内作关于原点对称的图形.(重点)
3.进一步体会数形结合的思想.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
(1)你能说出点P关于x轴对称点的坐标吗?
(2)你能说出点P关于y轴对称点的坐标吗?
点A与点B的位置关系是怎样的?点P与点C呢
讲授新知
贰
A′
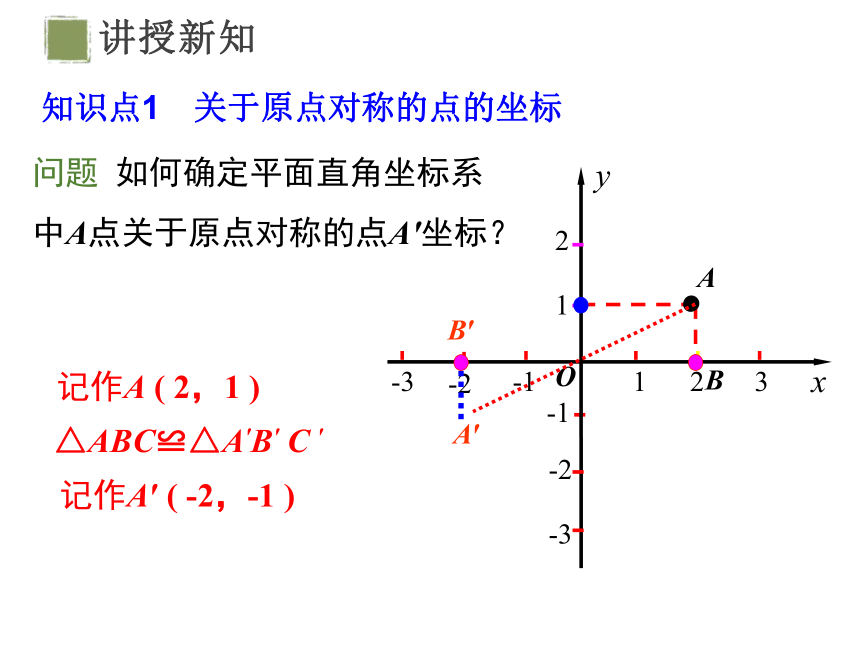
问题 如何确定平面直角坐标系中A点关于原点对称的点A′坐标?
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
A
记作A′ ( -2,-1 )
记作A ( 2,1 )
B
B′
△ABC≌△A′B′ C ′
知识点1 关于原点对称的点的坐标
讲授新知
x
y
O
-4 -3 -2 -1 1 2 3 4
-1
2
3
4
1
-2
-3
A
B
E
练一练:在直角坐标系中,作出点A(4,0) B(0,-3) C(2,1) D(-1,2) E(-3,-2)关于原点的对称点,并写出它们的坐标.
D
C
(-4,0)
(0,3)
(-2,-1)
(1,-2)
(3,2)
思考:关于原点对称的两个点的坐标之间有什么关系?
讲授新知
横坐标、纵坐标的符号都互为相反数,
关于原点对称的点的坐标关系特点
简记为:“关于谁,谁不变,关于原点都改变”.
即:点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
讲授新知
例1 已知点M(1-2m,m-1)关于原点的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )
C
范例应用
知识点2 利用关于原点对称的点的坐标关系作图
讲授新知
作关于原点对称的图形的步骤:
(1) 写出图形各顶点的坐标;
(2) 写出图形各顶点关于原点的对称点的坐标;
(3) 描点;
(4) 顺次连接;
(5) 下结论.
范例应用
例2 如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
关于原点的对称点的坐标分别为
A′(4,-1),B′(1,1),C′(3,-2)
依次连接A′B′ ,B′C′ ,C′ A′ ,
就可得到与△ABC关于原点对称
的△A′B′C′ .
解:△ABC的三个顶点的坐标分别为A(-4,1),B(-1, -1),C(-3,2),
当堂训练
叁
当堂训练
1.将平面直角坐标系内某个图形各个点的横坐标、纵坐标都乘以-1,所得图形与原图形的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.无法确定
2.已知矩形ABCD的对称中心恰为原点O,且点A的坐标为(2, -3),则点C的坐标为( )
A.(-2,3) B.(-2,-3) C.(2,3) D.(-3,2)
3.已知点P(-1,m2+1)与点Q关于原点对称,则点Q一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
C
A
D
当堂训练
4.已知点P(2a+b,-3a)与点P'(8,b+2).
若点P与点P'关于x轴对称,则a=_____ b=_______.
若点P与点P'关于y轴对称,则a=_____ b=_______.
若点P与点P'关于原点对称,则a=_____ b=_______.
5.点P(-3,1)关于原点的对称点P′的坐标是______ .
6.若P(5-2a,6)与Q(3,5b)关于原点对称,则a=___,b=____.
7.在如图所示编号为①、②、③、④的四
个三角形中,关于y轴对称的两个三角形
的编号为 ;关于坐标原点O对
称的两个三角形的编号为________.
y
x
-
1
-
2
-
4
-
3
-
5
-
1
-
2
-
4
-
5
-
3
1
2
4
3
5
1
2
4
3
5
O
①
②
③
④
2
4
6
-20
-1.2
-5.6
(3,-1)
4
①与②
①与③
课堂小结
肆
关于原点对称的点的坐标
特征
P(x,y)关于原点的对称点为P'(-x,-y).
作图
作出关于原点对称的图形,先求出对称点的坐标再描点画图.
课堂小结
课后作业
基础题:1.课后练习 P70第 3,4题。
提高题:2.学有余力的学生把练习册的提高题部分做了
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二十三章 旋 转
23.2.3 关于原点对称的点的坐标
23.2 中心对称
学习目标
1.掌握两点关于原点对称时,横纵坐标的关系.(难点)
2.会在平面直角坐标系内作关于原点对称的图形.(重点)
3.进一步体会数形结合的思想.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
(1)你能说出点P关于x轴对称点的坐标吗?
(2)你能说出点P关于y轴对称点的坐标吗?
点A与点B的位置关系是怎样的?点P与点C呢
讲授新知
贰
A′
问题 如何确定平面直角坐标系中A点关于原点对称的点A′坐标?
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
A
记作A′ ( -2,-1 )
记作A ( 2,1 )
B
B′
△ABC≌△A′B′ C ′
知识点1 关于原点对称的点的坐标
讲授新知
x
y
O
-4 -3 -2 -1 1 2 3 4
-1
2
3
4
1
-2
-3
A
B
E
练一练:在直角坐标系中,作出点A(4,0) B(0,-3) C(2,1) D(-1,2) E(-3,-2)关于原点的对称点,并写出它们的坐标.
D
C
(-4,0)
(0,3)
(-2,-1)
(1,-2)
(3,2)
思考:关于原点对称的两个点的坐标之间有什么关系?
讲授新知
横坐标、纵坐标的符号都互为相反数,
关于原点对称的点的坐标关系特点
简记为:“关于谁,谁不变,关于原点都改变”.
即:点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
讲授新知
例1 已知点M(1-2m,m-1)关于原点的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )
C
范例应用
知识点2 利用关于原点对称的点的坐标关系作图
讲授新知
作关于原点对称的图形的步骤:
(1) 写出图形各顶点的坐标;
(2) 写出图形各顶点关于原点的对称点的坐标;
(3) 描点;
(4) 顺次连接;
(5) 下结论.
范例应用
例2 如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
关于原点的对称点的坐标分别为
A′(4,-1),B′(1,1),C′(3,-2)
依次连接A′B′ ,B′C′ ,C′ A′ ,
就可得到与△ABC关于原点对称
的△A′B′C′ .
解:△ABC的三个顶点的坐标分别为A(-4,1),B(-1, -1),C(-3,2),
当堂训练
叁
当堂训练
1.将平面直角坐标系内某个图形各个点的横坐标、纵坐标都乘以-1,所得图形与原图形的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.无法确定
2.已知矩形ABCD的对称中心恰为原点O,且点A的坐标为(2, -3),则点C的坐标为( )
A.(-2,3) B.(-2,-3) C.(2,3) D.(-3,2)
3.已知点P(-1,m2+1)与点Q关于原点对称,则点Q一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
C
A
D
当堂训练
4.已知点P(2a+b,-3a)与点P'(8,b+2).
若点P与点P'关于x轴对称,则a=_____ b=_______.
若点P与点P'关于y轴对称,则a=_____ b=_______.
若点P与点P'关于原点对称,则a=_____ b=_______.
5.点P(-3,1)关于原点的对称点P′的坐标是______ .
6.若P(5-2a,6)与Q(3,5b)关于原点对称,则a=___,b=____.
7.在如图所示编号为①、②、③、④的四
个三角形中,关于y轴对称的两个三角形
的编号为 ;关于坐标原点O对
称的两个三角形的编号为________.
y
x
-
1
-
2
-
4
-
3
-
5
-
1
-
2
-
4
-
5
-
3
1
2
4
3
5
1
2
4
3
5
O
①
②
③
④
2
4
6
-20
-1.2
-5.6
(3,-1)
4
①与②
①与③
课堂小结
肆
关于原点对称的点的坐标
特征
P(x,y)关于原点的对称点为P'(-x,-y).
作图
作出关于原点对称的图形,先求出对称点的坐标再描点画图.
课堂小结
课后作业
基础题:1.课后练习 P70第 3,4题。
提高题:2.学有余力的学生把练习册的提高题部分做了
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
