北师大版物理八年级下册9_5探究—使用机械是否省功 学案课件(共25张PPT)
文档属性
| 名称 | 北师大版物理八年级下册9_5探究—使用机械是否省功 学案课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-17 10:48:47 | ||
图片预览






文档简介
(共25张PPT)
探究使用机械是否省功
导学设计
学点1 功的原理
阅读教材P112~P113。
问题与猜想:
问题:使用机械是否能省功?
猜想:使用机械不能省功。
理由:________________________________________。
省力的简单机械要费距离,省距离的简单机械要费力
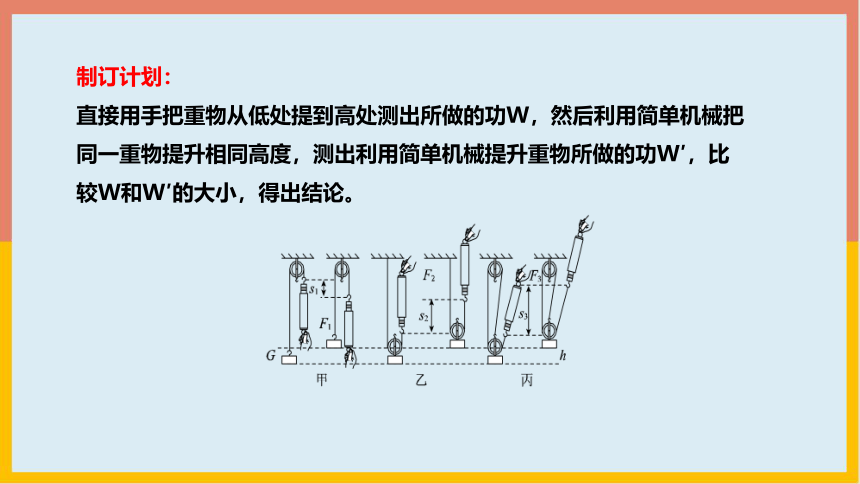
制订计划:
直接用手把重物从低处提到高处测出所做的功W,然后利用简单机械把同一重物提升相同高度,测出利用简单机械提升重物所做的功W′,比较W和W′的大小,得出结论。
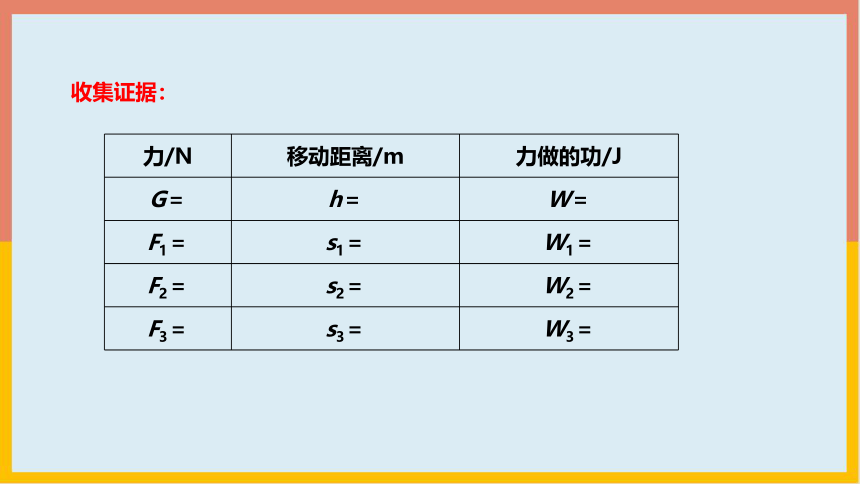
收集证据:
力/N 移动距离/m 力做的功/J
G= h= W=
F1= s1= W1=
F2= s2= W2=
F3= s3= W3=
分析与结论:
分析:利用上述简单机械提升重物所做的功总大于不用机械而直接用手提升重物时所做的功。
结论:_____________________。
理解:理想情况下,不计摩擦和机械自身的重力,W_____W′;
考虑摩擦和机械自身的重力,W_____W′。
使用任何机械都不省功
=
<
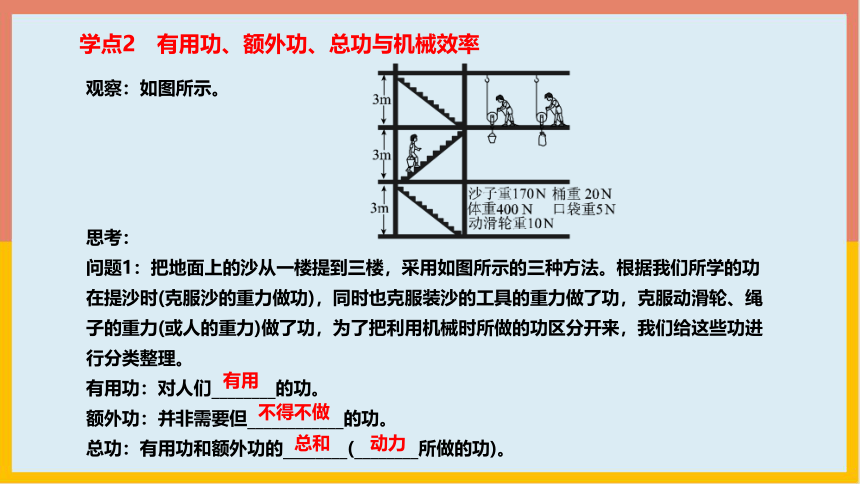
学点2 有用功、额外功、总功与机械效率
观察:如图所示。
思考:
问题1:把地面上的沙从一楼提到三楼,采用如图所示的三种方法。根据我们所学的功在提沙时(克服沙的重力做功),同时也克服装沙的工具的重力做了功,克服动滑轮、绳子的重力(或人的重力)做了功,为了把利用机械时所做的功区分开来,我们给这些功进行分类整理。
有用功:对人们________的功。
额外功:并非需要但____________的功。
总功:有用功和额外功的________(________所做的功)。
有用
不得不做
总和
动力
问题2:有用功、额外功、总功之间的关系:W总_____W有用+W额外。
问题3:为了把质量相同的沙提升相同的高度(有用功相同),利用不同方式提升时,人所做的功不同(总功不同)。有用功的比例大,说明机械的工作效率高。我们用有用功跟总功的比值来描述机械的这种特性,称之为____________。
问题4:机械效率的计算公式:η=________。
=
机械效率
问题5:机械效率一般用百分数表示,由于___________________________________________________________________,所以机械效率总是小于1。
在使用机械做功时,不可避免要做额外功,所以有用功要小于总功
学点3 斜面
观察:如图所示。
思考:
问题1:斜面是与__________成一角度的平面。
问题2:不计摩擦和机械自身的重力,根据功的原理FL=Gh,即F=,在直角三角形中L>h,所以利用斜面提升重物时,推力F________物体的重力G。斜面是一种可以________的简单机械。
问题3:“盘山公路”的目的是在物体的重力和斜面高度不变的情况下增大斜面的长度,可以__________。
水平面
小于
省力
更省力
类型一 使用机械是否省功
应用示例
例1 下列关于机械使用的说法中正确的是( )
A.使用机械的目的是省功
B.使用机械有时是为了省力,但不能省功
C.使用机械有时是为了省距离,也可省功
D.使用机械有时是为了改变力的方向,不能省力
B
[易混辨析]
使用简单机械可以省力,或者可以省距离,但省力必然费距离,
省距离必然费力,无论任何情况下,均不能省功。有时使用机械,既不省力,也不费力,但可以使做功方便,如改变力的方向。
类型二 认识有用功、额外功和机械效率
例2 如图所示,工人师傅用三种方法把重170 N的沙子提到三楼去。请根据图中所提供的信息计算(不考虑摩擦、滑轮重、绳重、桶重以及滑轮和口袋、桶的间距):
(1)三种方法所做的有用功是多少?
(2)第②种方法所做的额外功是多少?
(3)第②种方法的机械效率是多少?
[易混辨析]
区分有用功与额外功的关键是看我们做功的目的。
在同一做功过程中,目的不同,功的性质就不一样。例如用桶将水从水井中提出来,提水是我们的目的,而提桶是不需要的但又不得不做的功,故克服水的重力做的功是有用功,而克服桶的重力做的功是额外功;如果一只桶掉入水井里,我们要将桶从井中捞上来,则克服桶的重力做的功是有用功,而克服桶带出来的水的重力所做的功就是额外功了。
类型三 机械效率的计算
例3 如图所示的滑轮组,将重为350 N的物体竖直向上匀速提起0.2 m,人拉绳的力为250 N,求:
(1)人做的有用功、总功及额外功。
(2)此时滑轮组的机械效率。
(3)不计绳重和摩擦,动滑轮的重力。
[方法指导] 机械效率计算解题技巧:
(1)机械效率计算的要领:抓住四个基本量G、h、F、s,弄清机械中力之间的关系、距离之间的关系、功之间的关系。
(2)当不计绳重和摩擦时,求动滑轮的重力有两种方法。
从功的角度求解:额外功仅为克服动滑轮重做的功,
即W额外=G动h,G动=。
从力的角度求解:同一根绳子上的拉力处处相等,
由受力平衡得nF=G物+G动,则G动=nF-G物。
例4 现有重800 N的木箱A,小李同学想把它搬到高为6 m、长为10 m的斜面上,如图所示,他站在斜面上,沿斜面向上用600 N的拉力使木箱A以0.2 m/s的速度匀速从斜面底端到达斜面顶端。求:
(1)小李同学拉木箱的功率。
(2)该斜面的机械效率。
(3)木箱A在斜面上匀速运动时受到的摩擦力。
[方法指导] 解决其他机械的效率问题:
不论求哪种简单机械的效率,关键都是找出有用功、额外功、总功中的任意两个,然后利用公式η=求解。斜面中的额外功是克服斜面摩擦做的功,杠杆中的额外功是克服杠杆自重和转动时的摩擦做的功。
特别注意,在利用机械效率的相关知识求斜面上物体所受的摩擦力时,一般是先求出额外功,再利用W额外=fL的变形式求出摩擦力,绝对不能被“匀速直线运动”所“欺骗”,而误认为摩擦力和拉力相等。在斜面上的物体,因为重力和摩擦力方向不垂直,所以在平行于斜面的方向上还存在重力的分力,而拉力等于摩擦力和重力的分力之和。
课堂小结
探究—使用机械是否省功
探究实验
使用任何机械都不能省功
机械效率
有用功
额外功
总功
课堂反馈
1.使用简单机械( )
A.既可省力,又可省功
B.既可省距离,又可省功
C.都不省功
D.以上说法都不正确
C
2.如图所示,斜面长6 m,高1 m,工人沿斜面把重2400 N的箱子匀速推到车上(不计摩擦),推力对箱子做的功是______J,工人用的推力是_____N。
2400
400
3.李玲同学值日时用水桶提水从一楼上到三楼,她做的有用功是( ),额外功是( ),总功是( )
A.对人和桶所做的功
B.对水所做的功
C.对水和桶所做的功
D.对水、桶和人所做的功
B
A
D
4.机械效率越高,说明这个机械做功时( )
A.越省力
B.越快
C.越省功
D.有用功占总功的比例越大
D
5.用一个动滑轮将重为4 N的物体匀速提升1 m,拉力大小如图所示,则( )
A.拉力是2.2 N
B.有用功是2.2 J
C.总功是4.8 J
D.机械效率是120%
C
6.一台起重机将重1800 N的货物提高4 m,做的有用功为_______J,如果额外功是4800 J,总功为_______J,机械效率为________。
12000
7200
60%
再见
探究使用机械是否省功
导学设计
学点1 功的原理
阅读教材P112~P113。
问题与猜想:
问题:使用机械是否能省功?
猜想:使用机械不能省功。
理由:________________________________________。
省力的简单机械要费距离,省距离的简单机械要费力
制订计划:
直接用手把重物从低处提到高处测出所做的功W,然后利用简单机械把同一重物提升相同高度,测出利用简单机械提升重物所做的功W′,比较W和W′的大小,得出结论。
收集证据:
力/N 移动距离/m 力做的功/J
G= h= W=
F1= s1= W1=
F2= s2= W2=
F3= s3= W3=
分析与结论:
分析:利用上述简单机械提升重物所做的功总大于不用机械而直接用手提升重物时所做的功。
结论:_____________________。
理解:理想情况下,不计摩擦和机械自身的重力,W_____W′;
考虑摩擦和机械自身的重力,W_____W′。
使用任何机械都不省功
=
<
学点2 有用功、额外功、总功与机械效率
观察:如图所示。
思考:
问题1:把地面上的沙从一楼提到三楼,采用如图所示的三种方法。根据我们所学的功在提沙时(克服沙的重力做功),同时也克服装沙的工具的重力做了功,克服动滑轮、绳子的重力(或人的重力)做了功,为了把利用机械时所做的功区分开来,我们给这些功进行分类整理。
有用功:对人们________的功。
额外功:并非需要但____________的功。
总功:有用功和额外功的________(________所做的功)。
有用
不得不做
总和
动力
问题2:有用功、额外功、总功之间的关系:W总_____W有用+W额外。
问题3:为了把质量相同的沙提升相同的高度(有用功相同),利用不同方式提升时,人所做的功不同(总功不同)。有用功的比例大,说明机械的工作效率高。我们用有用功跟总功的比值来描述机械的这种特性,称之为____________。
问题4:机械效率的计算公式:η=________。
=
机械效率
问题5:机械效率一般用百分数表示,由于___________________________________________________________________,所以机械效率总是小于1。
在使用机械做功时,不可避免要做额外功,所以有用功要小于总功
学点3 斜面
观察:如图所示。
思考:
问题1:斜面是与__________成一角度的平面。
问题2:不计摩擦和机械自身的重力,根据功的原理FL=Gh,即F=,在直角三角形中L>h,所以利用斜面提升重物时,推力F________物体的重力G。斜面是一种可以________的简单机械。
问题3:“盘山公路”的目的是在物体的重力和斜面高度不变的情况下增大斜面的长度,可以__________。
水平面
小于
省力
更省力
类型一 使用机械是否省功
应用示例
例1 下列关于机械使用的说法中正确的是( )
A.使用机械的目的是省功
B.使用机械有时是为了省力,但不能省功
C.使用机械有时是为了省距离,也可省功
D.使用机械有时是为了改变力的方向,不能省力
B
[易混辨析]
使用简单机械可以省力,或者可以省距离,但省力必然费距离,
省距离必然费力,无论任何情况下,均不能省功。有时使用机械,既不省力,也不费力,但可以使做功方便,如改变力的方向。
类型二 认识有用功、额外功和机械效率
例2 如图所示,工人师傅用三种方法把重170 N的沙子提到三楼去。请根据图中所提供的信息计算(不考虑摩擦、滑轮重、绳重、桶重以及滑轮和口袋、桶的间距):
(1)三种方法所做的有用功是多少?
(2)第②种方法所做的额外功是多少?
(3)第②种方法的机械效率是多少?
[易混辨析]
区分有用功与额外功的关键是看我们做功的目的。
在同一做功过程中,目的不同,功的性质就不一样。例如用桶将水从水井中提出来,提水是我们的目的,而提桶是不需要的但又不得不做的功,故克服水的重力做的功是有用功,而克服桶的重力做的功是额外功;如果一只桶掉入水井里,我们要将桶从井中捞上来,则克服桶的重力做的功是有用功,而克服桶带出来的水的重力所做的功就是额外功了。
类型三 机械效率的计算
例3 如图所示的滑轮组,将重为350 N的物体竖直向上匀速提起0.2 m,人拉绳的力为250 N,求:
(1)人做的有用功、总功及额外功。
(2)此时滑轮组的机械效率。
(3)不计绳重和摩擦,动滑轮的重力。
[方法指导] 机械效率计算解题技巧:
(1)机械效率计算的要领:抓住四个基本量G、h、F、s,弄清机械中力之间的关系、距离之间的关系、功之间的关系。
(2)当不计绳重和摩擦时,求动滑轮的重力有两种方法。
从功的角度求解:额外功仅为克服动滑轮重做的功,
即W额外=G动h,G动=。
从力的角度求解:同一根绳子上的拉力处处相等,
由受力平衡得nF=G物+G动,则G动=nF-G物。
例4 现有重800 N的木箱A,小李同学想把它搬到高为6 m、长为10 m的斜面上,如图所示,他站在斜面上,沿斜面向上用600 N的拉力使木箱A以0.2 m/s的速度匀速从斜面底端到达斜面顶端。求:
(1)小李同学拉木箱的功率。
(2)该斜面的机械效率。
(3)木箱A在斜面上匀速运动时受到的摩擦力。
[方法指导] 解决其他机械的效率问题:
不论求哪种简单机械的效率,关键都是找出有用功、额外功、总功中的任意两个,然后利用公式η=求解。斜面中的额外功是克服斜面摩擦做的功,杠杆中的额外功是克服杠杆自重和转动时的摩擦做的功。
特别注意,在利用机械效率的相关知识求斜面上物体所受的摩擦力时,一般是先求出额外功,再利用W额外=fL的变形式求出摩擦力,绝对不能被“匀速直线运动”所“欺骗”,而误认为摩擦力和拉力相等。在斜面上的物体,因为重力和摩擦力方向不垂直,所以在平行于斜面的方向上还存在重力的分力,而拉力等于摩擦力和重力的分力之和。
课堂小结
探究—使用机械是否省功
探究实验
使用任何机械都不能省功
机械效率
有用功
额外功
总功
课堂反馈
1.使用简单机械( )
A.既可省力,又可省功
B.既可省距离,又可省功
C.都不省功
D.以上说法都不正确
C
2.如图所示,斜面长6 m,高1 m,工人沿斜面把重2400 N的箱子匀速推到车上(不计摩擦),推力对箱子做的功是______J,工人用的推力是_____N。
2400
400
3.李玲同学值日时用水桶提水从一楼上到三楼,她做的有用功是( ),额外功是( ),总功是( )
A.对人和桶所做的功
B.对水所做的功
C.对水和桶所做的功
D.对水、桶和人所做的功
B
A
D
4.机械效率越高,说明这个机械做功时( )
A.越省力
B.越快
C.越省功
D.有用功占总功的比例越大
D
5.用一个动滑轮将重为4 N的物体匀速提升1 m,拉力大小如图所示,则( )
A.拉力是2.2 N
B.有用功是2.2 J
C.总功是4.8 J
D.机械效率是120%
C
6.一台起重机将重1800 N的货物提高4 m,做的有用功为_______J,如果额外功是4800 J,总功为_______J,机械效率为________。
12000
7200
60%
再见
