24.1.1圆 课件(共25张PPT)
图片预览







文档简介
(共25张PPT)
第二十四章 圆
24.1.1 圆
24.1. 圆的有关性质
学习目标
1.认识圆,理解圆的本质属性. (重点)
2.理解弦、弧、半圆、优弧、劣弧、同心圆、等圆等弧等与圆有关的概念,并了解它们之间的区别和联系.(难点)
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
车轮、齿轮、水杯等常见物品为什么做成圆形的?从这节课开始就来进一步认识圆,研究圆的有关性质,用圆的知识解决一些实际问题.
讲授新知
贰
讲授新知
知识点1 圆的定义
1.如图,在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.
O
A
·
r
固定的端点 O 叫做圆心;
线段 OA 叫做半径;
以点 O 为圆心的圆,记作⊙O,读作“圆O”.
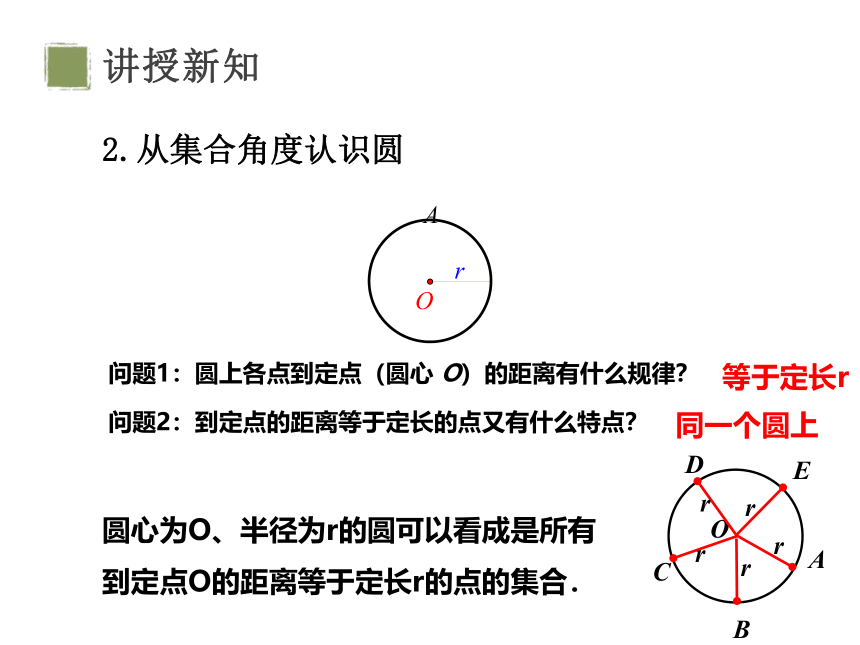
2.从集合角度认识圆
问题1:圆上各点到定点(圆心 O)的距离有什么规律?
问题2:到定点的距离等于定长的点又有什么特点?
·
r
O
A
讲授新知
等于定长r
同一个圆上
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
O
·
A
C
E
r
r
r
r
r
D
B
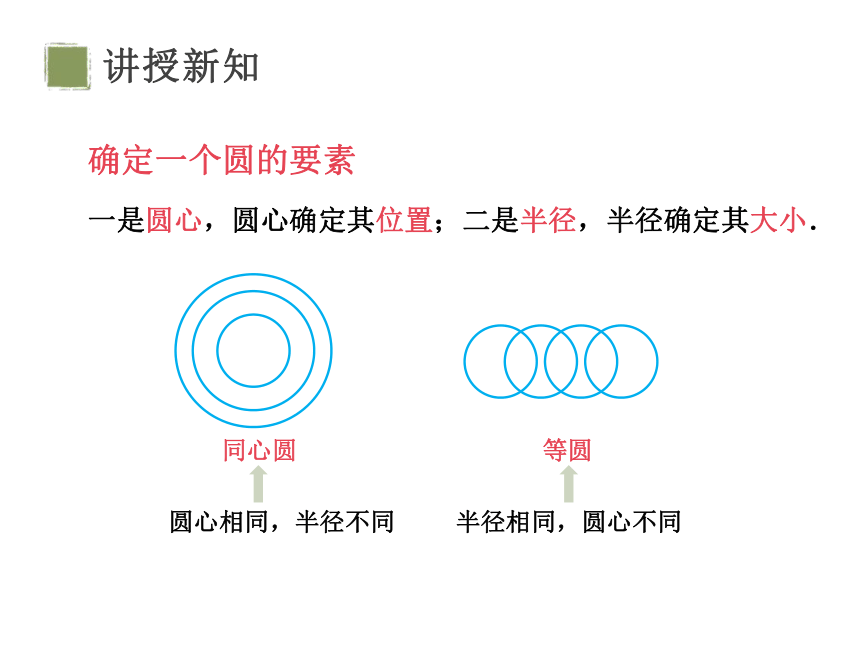
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
讲授新知
例1 矩形ABCD的对角线AC、BD相交于O.求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
范例应用
练一练
下列条件中,可以确定一个圆的是( )
D
A.半径为1 cm
B.圆心在点O处
C.半径是1 cm,且经过点P
D.圆心在点O处,且直径是2 cm
范例应用
·
C
O
A
B
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
讲授新知
知识点2 与圆有关的概念
O
A
B
O
A
B
圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
O
A
B
C
O
A
B
C
D
O
A
B
C
D
直径是最长的弦
讲授新知
知识点
·
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
C
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧.
以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
小于半圆的弧叫做劣弧,如图中的AC ;
(
大于半圆的弧叫做优弧,如图中的ABC.
(
讲授新知
例2 如图.
(1)请写出以点A为端点的优弧及劣弧;
(2)请写出以点A为端点的弦及直径.
弦AF,AB,AC.其中弦AB又是直径.
(3)请任选一条弦,写出这条弦所对的弧.
答案不唯一,如:弦AF,它所对的弧是 .
A
B
C
E
F
D
O
劣弧:
优弧:
AF,
(
AD,
(
AC,
(
AE.
(
AFE,
(
AFC,
(
ADE,
(
ADC.
(
AF
(
范例应用
当堂训练
叁
1.下列说法正确的是( )
A.直径是弦,弦是直径
B.半圆是弧,弧是半圆
C.弦是圆上两点之间的部分
D.半径不是弦,直径是最长的弦
D
2.下列说法中,不正确的是( )
A.过圆心的弦是圆的直径
B.等弧的长度一定相等
C.周长相等的两个圆是等圆
D.长度相等的两条弧是等弧
D
当堂训练
3.一个圆的最大弦长是10cm,则此圆的半径是 cm.
4.在同一平面内与已知点A的距离等于5cm的所有点所组成的图形是 .
5.如图所示,以AB为直径的半圆O上有两点D、E,ED与BA的延长线相交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是 .
5
圆
60°
当堂训练
6.已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.
求证:OC=OD.
证明:∵OA、OB为⊙O的半径,
∴OA=OB. ∴∠A=∠B.
又∵AC=BD,
∴△ACO≌△BDO.
∴OC=OD.
当堂训练
课堂小结
肆
圆
定义
旋转定义
要画一个确定的圆,关键是确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
今天我们学习了哪些知识?
课堂小结
课后作业
基础题:1.课后习题 P81第 1,2,3题。
提高题:2.请学有余力的同学同步训练习题
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二十四章 圆
24.1.1 圆
24.1. 圆的有关性质
学习目标
1.认识圆,理解圆的本质属性. (重点)
2.理解弦、弧、半圆、优弧、劣弧、同心圆、等圆等弧等与圆有关的概念,并了解它们之间的区别和联系.(难点)
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
车轮、齿轮、水杯等常见物品为什么做成圆形的?从这节课开始就来进一步认识圆,研究圆的有关性质,用圆的知识解决一些实际问题.
讲授新知
贰
讲授新知
知识点1 圆的定义
1.如图,在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.
O
A
·
r
固定的端点 O 叫做圆心;
线段 OA 叫做半径;
以点 O 为圆心的圆,记作⊙O,读作“圆O”.
2.从集合角度认识圆
问题1:圆上各点到定点(圆心 O)的距离有什么规律?
问题2:到定点的距离等于定长的点又有什么特点?
·
r
O
A
讲授新知
等于定长r
同一个圆上
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
O
·
A
C
E
r
r
r
r
r
D
B
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
讲授新知
例1 矩形ABCD的对角线AC、BD相交于O.求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
范例应用
练一练
下列条件中,可以确定一个圆的是( )
D
A.半径为1 cm
B.圆心在点O处
C.半径是1 cm,且经过点P
D.圆心在点O处,且直径是2 cm
范例应用
·
C
O
A
B
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
讲授新知
知识点2 与圆有关的概念
O
A
B
O
A
B
圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
O
A
B
C
O
A
B
C
D
O
A
B
C
D
直径是最长的弦
讲授新知
知识点
·
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
C
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧.
以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
小于半圆的弧叫做劣弧,如图中的AC ;
(
大于半圆的弧叫做优弧,如图中的ABC.
(
讲授新知
例2 如图.
(1)请写出以点A为端点的优弧及劣弧;
(2)请写出以点A为端点的弦及直径.
弦AF,AB,AC.其中弦AB又是直径.
(3)请任选一条弦,写出这条弦所对的弧.
答案不唯一,如:弦AF,它所对的弧是 .
A
B
C
E
F
D
O
劣弧:
优弧:
AF,
(
AD,
(
AC,
(
AE.
(
AFE,
(
AFC,
(
ADE,
(
ADC.
(
AF
(
范例应用
当堂训练
叁
1.下列说法正确的是( )
A.直径是弦,弦是直径
B.半圆是弧,弧是半圆
C.弦是圆上两点之间的部分
D.半径不是弦,直径是最长的弦
D
2.下列说法中,不正确的是( )
A.过圆心的弦是圆的直径
B.等弧的长度一定相等
C.周长相等的两个圆是等圆
D.长度相等的两条弧是等弧
D
当堂训练
3.一个圆的最大弦长是10cm,则此圆的半径是 cm.
4.在同一平面内与已知点A的距离等于5cm的所有点所组成的图形是 .
5.如图所示,以AB为直径的半圆O上有两点D、E,ED与BA的延长线相交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是 .
5
圆
60°
当堂训练
6.已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.
求证:OC=OD.
证明:∵OA、OB为⊙O的半径,
∴OA=OB. ∴∠A=∠B.
又∵AC=BD,
∴△ACO≌△BDO.
∴OC=OD.
当堂训练
课堂小结
肆
圆
定义
旋转定义
要画一个确定的圆,关键是确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
今天我们学习了哪些知识?
课堂小结
课后作业
基础题:1.课后习题 P81第 1,2,3题。
提高题:2.请学有余力的同学同步训练习题
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
