24.2.1 点和圆的位置关系 课件(共27张PPT)
文档属性
| 名称 | 24.2.1 点和圆的位置关系 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 13:42:13 | ||
图片预览






文档简介
(共27张PPT)
第二十四章 圆
24.2.1 点与圆的位置关系
24.2 点和圆、直线和圆的位置关系
学习目标
1.理解并掌握点和圆的三种位置关系. (难点)
2.理解不在同一直线上的三个点确定一个圆及其运用. (重点)
3.了解三角形的外接圆和三角形外心的概念.
4.了解反证法的证明思想.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
问题: 观察下列图片.是一个小朋友玩飞镖游戏时在靶子上留下的小孔,这些小孔和这些同心圆是什么关系呢?
新课导入
讲授新知
贰
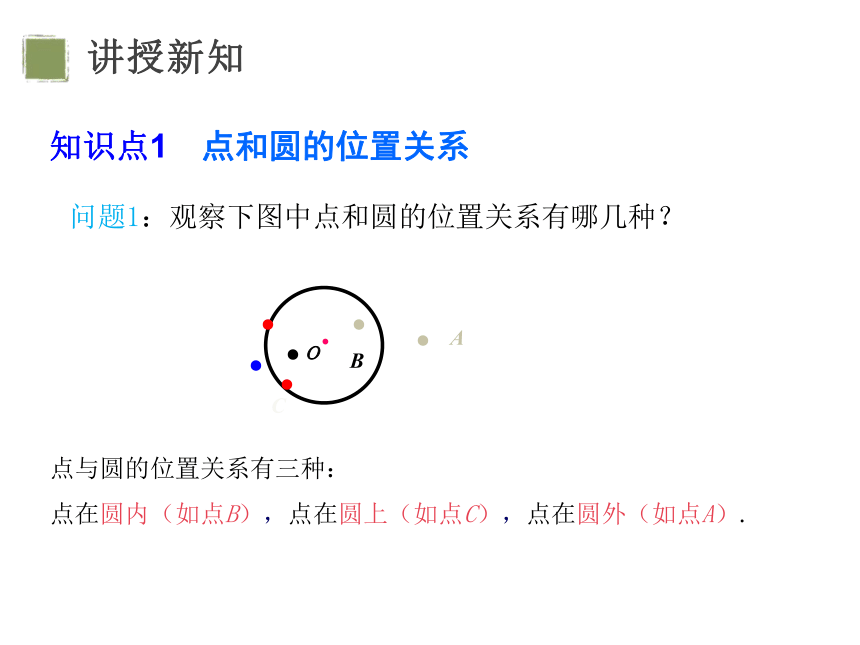
问题1:观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
. B
.A
.
点与圆的位置关系有三种:
点在圆内(如点B),点在圆上(如点C),点在圆外(如点A).
知识点1 点和圆的位置关系
讲授新知
dd=r
d>r
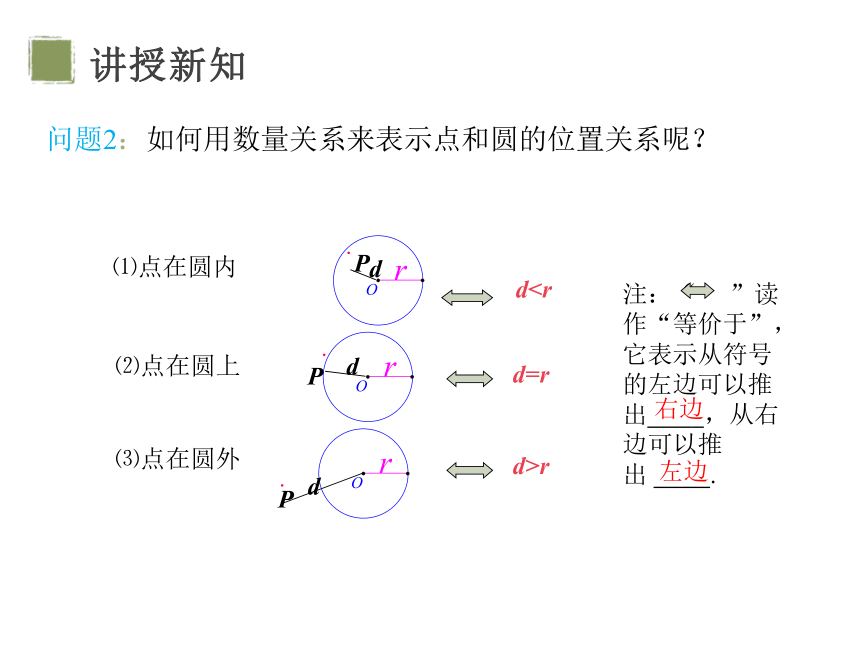
问题2:如何用数量关系来表示点和圆的位置关系呢?
⑴点在圆内
·
P
⑵点在圆上
·
P
⑶点在圆外
·
P
d
d
d
注:“ ”读作“等价于”,它表示从符号的左边可以推出 ,从右边可以推出 .
右边
左边
讲授新知
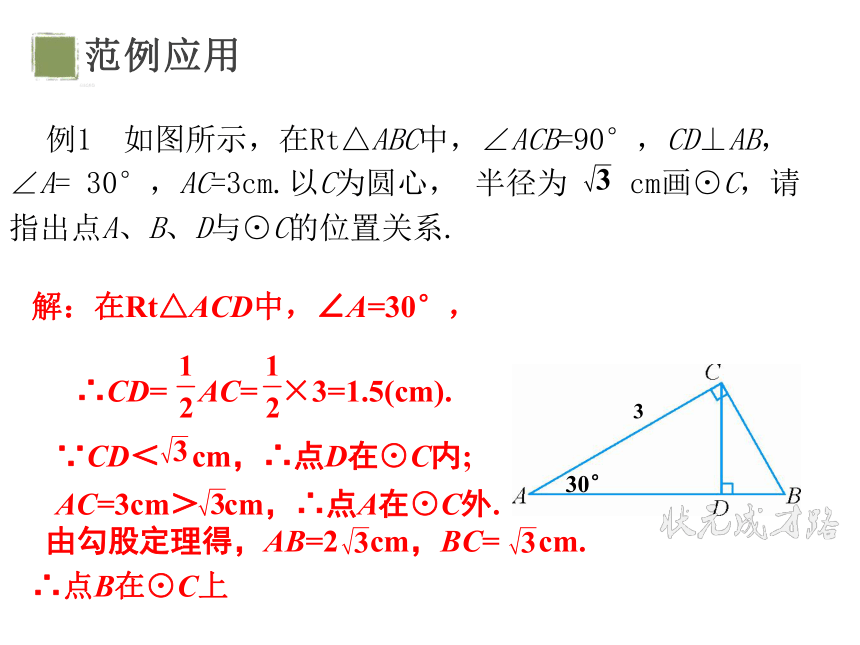
例1 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A= 30°,AC=3cm.以C为圆心, 半径为 cm画⊙C,请指出点A、B、D与⊙C的位置关系.
3
30°
解:在Rt△ACD中,∠A=30°,
∴点B在⊙C上
∴CD= AC= ×3=1.5(cm).
∵CD< cm,∴点D在⊙C内;
AC=3cm> cm,∴点A在⊙C外.
由勾股定理得,AB=2 cm,BC= cm.
范例应用
1. 作经过已知点A的圆,你能作出多少个圆?圆心在哪里?半径多大?
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离.
已知圆心和半径,可以作一个圆.
知识点2 确定圆的条件
讲授新知
2. 作经过已知点A、B的圆,你能作出多少个?圆心在哪里?
●
O
O
●
●
O
●
O
A
B
无数个,它们的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
讲授新知
3. 经过同一平面内三个点作圆,情况会怎样呢?
经过不在同一直线上的三点A、B、C能作出几个圆?圆心在哪里?
不在同一直线上的三个点确定一个圆.
┓
┏
●
B
●C
●A
●O
讲授新知
已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
O
知识点3 三角形的外接圆
1.作三角形任意两边的垂直平分线,确定其交点;
2.以该交点为圆心,交点到三个顶点中任意一点的距离为半径作圆即可.
讲授新知
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
讲授新知
1. 外接圆与内接三角形
⊙O叫做△ABC的外接圆,
△ABC叫做⊙O的内接三角形.
到三角形三个顶点的距离相等.
2.三角形的外心
●O
A
B
C
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三边垂直平分线的交点.
性质:
一个圆可以有无数个内接三角形,但是一个三角形只有一个外接圆.
定义:
讲授新知
例2 如图, ⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4.求AC的长.
范例应用
经过同一条直线上的三个点能作出一个圆吗?
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A,B,C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l 这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
l
知识点4 反证法
讲授新知
反证法的定义
先假设命题的结论不成立,然后经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
反证法的一般步骤
假设命题的结论不成立,
从这个假设出发,经过推理,得出矛盾,
由矛盾判定假设不正确,从而肯定原命题的结论正确.
讲授新知
当堂训练
叁
2.若一个三角形的外心在一边上,则此三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
3.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
B
1.判断下列说法是否正确:
(1) 任意的一个三角形一定有一个外接圆.( )
(2) 任意一个圆有且只有一个内接三角形.( )
(3) 经过三点一定可以确定一个圆.( )
(4) 三角形的外心到三角形各顶点的距离相等.( )
√
×
×
√
当堂训练
4.爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域,已知这个导火索的长度为18cm,点导火索的人以每秒6.5m的速度撤离是否安全?为什么?
解:由题意可知,导火索燃烧完需18÷0.9=20(S).
又点导火索的人以每秒6.5m的速度撤离,
则导火索燃烧完时撤离的最大距离为6.5×20=130(m).
∵130>120,∴安全.
当堂训练
课堂小结
肆
点和圆的位置关系
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
确定圆的条件:
不在同一直线上的三个点确定一个圆.
反证法:
①反设,②推导出矛盾,③下结论
课堂小结
课后作业
基础题:1.课后习题 P101页1、7、8题
提高题:2.请学有余力的同学同步训练习题
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二十四章 圆
24.2.1 点与圆的位置关系
24.2 点和圆、直线和圆的位置关系
学习目标
1.理解并掌握点和圆的三种位置关系. (难点)
2.理解不在同一直线上的三个点确定一个圆及其运用. (重点)
3.了解三角形的外接圆和三角形外心的概念.
4.了解反证法的证明思想.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
问题: 观察下列图片.是一个小朋友玩飞镖游戏时在靶子上留下的小孔,这些小孔和这些同心圆是什么关系呢?
新课导入
讲授新知
贰
问题1:观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
. B
.A
.
点与圆的位置关系有三种:
点在圆内(如点B),点在圆上(如点C),点在圆外(如点A).
知识点1 点和圆的位置关系
讲授新知
d
d>r
问题2:如何用数量关系来表示点和圆的位置关系呢?
⑴点在圆内
·
P
⑵点在圆上
·
P
⑶点在圆外
·
P
d
d
d
注:“ ”读作“等价于”,它表示从符号的左边可以推出 ,从右边可以推出 .
右边
左边
讲授新知
例1 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A= 30°,AC=3cm.以C为圆心, 半径为 cm画⊙C,请指出点A、B、D与⊙C的位置关系.
3
30°
解:在Rt△ACD中,∠A=30°,
∴点B在⊙C上
∴CD= AC= ×3=1.5(cm).
∵CD< cm,∴点D在⊙C内;
AC=3cm> cm,∴点A在⊙C外.
由勾股定理得,AB=2 cm,BC= cm.
范例应用
1. 作经过已知点A的圆,你能作出多少个圆?圆心在哪里?半径多大?
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离.
已知圆心和半径,可以作一个圆.
知识点2 确定圆的条件
讲授新知
2. 作经过已知点A、B的圆,你能作出多少个?圆心在哪里?
●
O
O
●
●
O
●
O
A
B
无数个,它们的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
讲授新知
3. 经过同一平面内三个点作圆,情况会怎样呢?
经过不在同一直线上的三点A、B、C能作出几个圆?圆心在哪里?
不在同一直线上的三个点确定一个圆.
┓
┏
●
B
●C
●A
●O
讲授新知
已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
O
知识点3 三角形的外接圆
1.作三角形任意两边的垂直平分线,确定其交点;
2.以该交点为圆心,交点到三个顶点中任意一点的距离为半径作圆即可.
讲授新知
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
讲授新知
1. 外接圆与内接三角形
⊙O叫做△ABC的外接圆,
△ABC叫做⊙O的内接三角形.
到三角形三个顶点的距离相等.
2.三角形的外心
●O
A
B
C
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三边垂直平分线的交点.
性质:
一个圆可以有无数个内接三角形,但是一个三角形只有一个外接圆.
定义:
讲授新知
例2 如图, ⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4.求AC的长.
范例应用
经过同一条直线上的三个点能作出一个圆吗?
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A,B,C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l 这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
l
知识点4 反证法
讲授新知
反证法的定义
先假设命题的结论不成立,然后经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
反证法的一般步骤
假设命题的结论不成立,
从这个假设出发,经过推理,得出矛盾,
由矛盾判定假设不正确,从而肯定原命题的结论正确.
讲授新知
当堂训练
叁
2.若一个三角形的外心在一边上,则此三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
3.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
B
1.判断下列说法是否正确:
(1) 任意的一个三角形一定有一个外接圆.( )
(2) 任意一个圆有且只有一个内接三角形.( )
(3) 经过三点一定可以确定一个圆.( )
(4) 三角形的外心到三角形各顶点的距离相等.( )
√
×
×
√
当堂训练
4.爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域,已知这个导火索的长度为18cm,点导火索的人以每秒6.5m的速度撤离是否安全?为什么?
解:由题意可知,导火索燃烧完需18÷0.9=20(S).
又点导火索的人以每秒6.5m的速度撤离,
则导火索燃烧完时撤离的最大距离为6.5×20=130(m).
∵130>120,∴安全.
当堂训练
课堂小结
肆
点和圆的位置关系
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
确定圆的条件:
不在同一直线上的三个点确定一个圆.
反证法:
①反设,②推导出矛盾,③下结论
课堂小结
课后作业
基础题:1.课后习题 P101页1、7、8题
提高题:2.请学有余力的同学同步训练习题
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
