24.3 正多边形和圆 课件(共24张PPT)
文档属性
| 名称 | 24.3 正多边形和圆 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 17:22:12 | ||
图片预览







文档简介
(共24张PPT)
第二十四章 圆
24.3 正多边形和圆
学习目标
1.理解并掌握正多边形的半径和边长、边心距、
中心角之间的关系. (重点)
2.会进行特殊的与正多边形有关的计算,会画
某些正多边形. (难点)
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
情景:欣赏下面图片.
问题:什么叫正多边形?图中有哪些正多边形?正多边形与圆有哪些关系?
新课导入
讲授新知
贰
什么叫做正多边形?
各边相等、各角也相等的多边形叫做正多边形.
矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
正多边形
各边相等
各角相等
缺一不可
讲授新知
知识点1 圆内接正多边形
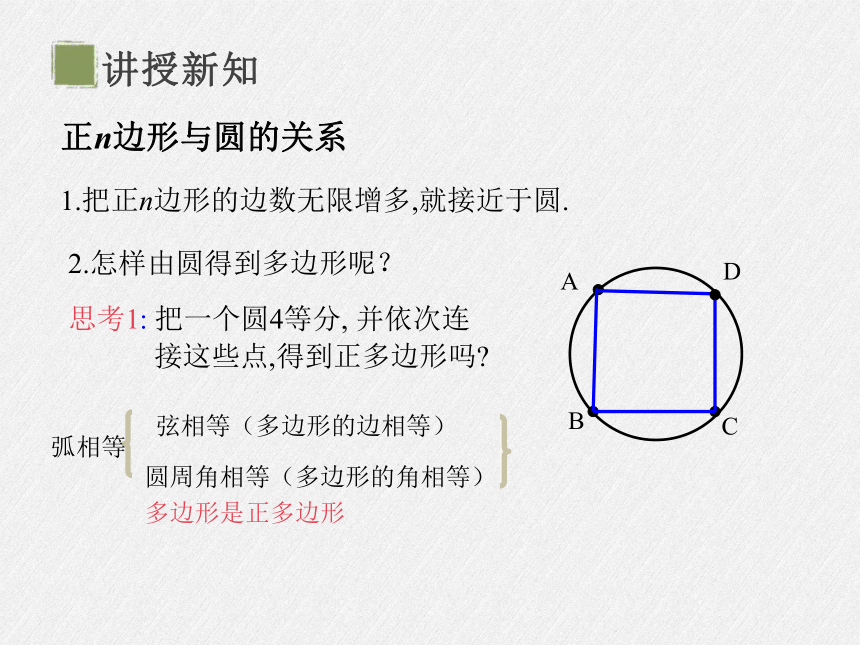
正n边形与圆的关系
1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢?
A
B
C
D
思考1: 把一个圆4等分, 并依次连
接这些点,得到正多边形吗
弧相等
弦相等(多边形的边相等)
圆周角相等(多边形的角相等)
多边形是正多边形
讲授新知
③ ∠A ∠E
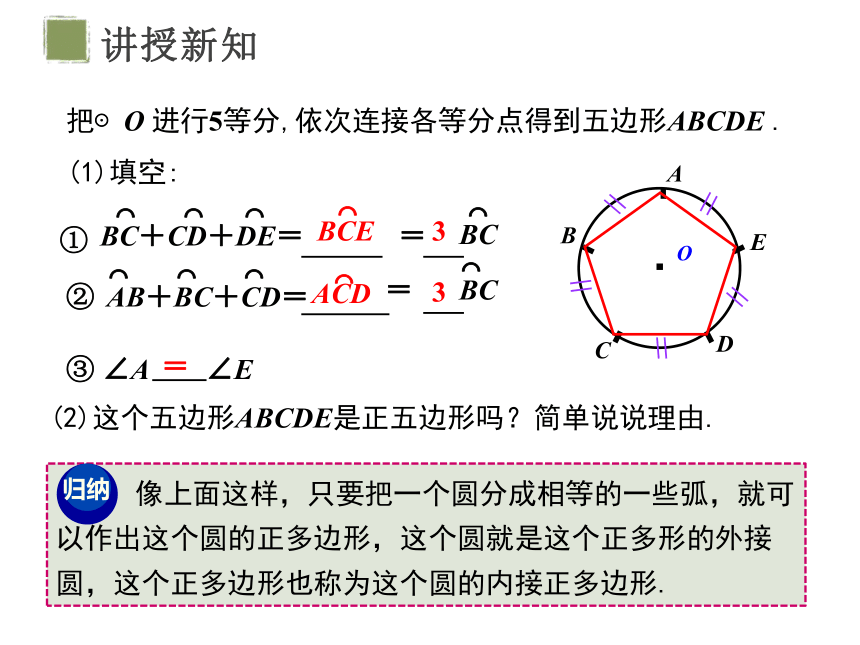
把⊙O 进行5等分,依次连接各等分点得到五边形ABCDE .
(1)填空:
·
A
O
E
D
C
B
⌒
BCE
⌒
BC
AB+BC+CD=
⌒
⌒
⌒
②
=
⌒
BC
BC+CD+DE=
⌒
⌒
⌒
①
=
3
3
=
ACD
⌒
(2)这个五边形ABCDE是正五边形吗?简单说说理由.
像上面这样,只要把一个圆分成相等的一些弧,就可以作出这个圆的正多边形,这个圆就是这个正多形的外接圆,这个正多边形也称为这个圆的内接正多边形.
归纳
讲授新知
例1 下列说法中,不正确的是( )
A.正多边形一定有一个外接圆和一个内切圆
B.各边相等且各角相等的多边形是正多边形
C.正多边形的内切圆和外接圆是同心圆
D.正多边形既是轴对称图形,又是中心对称图形
D
范例应用
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:
一个正多边形的外接圆的圆心.
正多边形的半径: 外接圆的半径
正多边形的中心角:
正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
知识点2 圆内接正多边形的有关概念
讲授新知
2.作边心距,构造直角三角形.
1.连半径,得中心角;
O
A
B
C
D
E
F
R
M
r
·
圆内接正多边形的辅助线
O
边心距r
边长一半
半径R
C
M
中心角一半
讲授新知
例2 如图,已知半径为4的圆内接正六边形ABCDEF:
①它的中心角等于 度 ;
② OC BC (填>、<或=);
③△OBC是 三角形;
④圆内接正六边形的面积是
△OBC面积的 倍.
⑤圆内接正n边形面积公式:________________________.
C
D
O
B
E
F
A
P
60
=
等边
6
知识点3 正多边形的有关计算
讲授新知
例3 有一个亭子,它的地基半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).
因此,亭子地基的周长
l =4×6=24(m).
解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.
范例应用
利用勾股定理,可得边心距
亭子地基的面积
在Rt△OPC中,OC=4,PC=
范例应用
当堂训练
叁
1.下列说法中正确的是( )
A.各边都相等的多边形是正多边形
B.正多边形既是轴对称图形,又是中心对称图形
C.各边都相等的圆内接多边形是正多边形
D.各角都相等的圆内接多边形是正多边形
C
2.如果一个正多边形的每个外角都等于36°,则这个多边形的中心角等于( )
A.36° B.18° C.72° D.54°
3.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使直角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能
取值的个数是( )
A.4 B.5 C.6 D.7
A
B
当堂训练
4.如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为多少?
解:如图,∠ABC=120°. AB=BC=a, AC=b.
过B作BD⊥AC于点D,
则AD=DC= b.
在Rt△ABD中,∠BAC=30°,
∴BD= AB=3mm.
∴b=2AD=6 mm.
即扳手张开的开口b至少要6 mm.
A
C
B D
当堂训练
课堂小结
肆
正多边形
正多边形的定义与对称性
正多边形的有
关概念及性质
①正多边形的内角和=
②中心角=
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
课堂小结
课后作业
基础题:1.课后习题 24.3的复习巩固
提高题:2.请学有余力的同学做P108”综合运用”
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二十四章 圆
24.3 正多边形和圆
学习目标
1.理解并掌握正多边形的半径和边长、边心距、
中心角之间的关系. (重点)
2.会进行特殊的与正多边形有关的计算,会画
某些正多边形. (难点)
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
情景:欣赏下面图片.
问题:什么叫正多边形?图中有哪些正多边形?正多边形与圆有哪些关系?
新课导入
讲授新知
贰
什么叫做正多边形?
各边相等、各角也相等的多边形叫做正多边形.
矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
正多边形
各边相等
各角相等
缺一不可
讲授新知
知识点1 圆内接正多边形
正n边形与圆的关系
1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢?
A
B
C
D
思考1: 把一个圆4等分, 并依次连
接这些点,得到正多边形吗
弧相等
弦相等(多边形的边相等)
圆周角相等(多边形的角相等)
多边形是正多边形
讲授新知
③ ∠A ∠E
把⊙O 进行5等分,依次连接各等分点得到五边形ABCDE .
(1)填空:
·
A
O
E
D
C
B
⌒
BCE
⌒
BC
AB+BC+CD=
⌒
⌒
⌒
②
=
⌒
BC
BC+CD+DE=
⌒
⌒
⌒
①
=
3
3
=
ACD
⌒
(2)这个五边形ABCDE是正五边形吗?简单说说理由.
像上面这样,只要把一个圆分成相等的一些弧,就可以作出这个圆的正多边形,这个圆就是这个正多形的外接圆,这个正多边形也称为这个圆的内接正多边形.
归纳
讲授新知
例1 下列说法中,不正确的是( )
A.正多边形一定有一个外接圆和一个内切圆
B.各边相等且各角相等的多边形是正多边形
C.正多边形的内切圆和外接圆是同心圆
D.正多边形既是轴对称图形,又是中心对称图形
D
范例应用
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:
一个正多边形的外接圆的圆心.
正多边形的半径: 外接圆的半径
正多边形的中心角:
正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
知识点2 圆内接正多边形的有关概念
讲授新知
2.作边心距,构造直角三角形.
1.连半径,得中心角;
O
A
B
C
D
E
F
R
M
r
·
圆内接正多边形的辅助线
O
边心距r
边长一半
半径R
C
M
中心角一半
讲授新知
例2 如图,已知半径为4的圆内接正六边形ABCDEF:
①它的中心角等于 度 ;
② OC BC (填>、<或=);
③△OBC是 三角形;
④圆内接正六边形的面积是
△OBC面积的 倍.
⑤圆内接正n边形面积公式:________________________.
C
D
O
B
E
F
A
P
60
=
等边
6
知识点3 正多边形的有关计算
讲授新知
例3 有一个亭子,它的地基半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).
因此,亭子地基的周长
l =4×6=24(m).
解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.
范例应用
利用勾股定理,可得边心距
亭子地基的面积
在Rt△OPC中,OC=4,PC=
范例应用
当堂训练
叁
1.下列说法中正确的是( )
A.各边都相等的多边形是正多边形
B.正多边形既是轴对称图形,又是中心对称图形
C.各边都相等的圆内接多边形是正多边形
D.各角都相等的圆内接多边形是正多边形
C
2.如果一个正多边形的每个外角都等于36°,则这个多边形的中心角等于( )
A.36° B.18° C.72° D.54°
3.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使直角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能
取值的个数是( )
A.4 B.5 C.6 D.7
A
B
当堂训练
4.如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为多少?
解:如图,∠ABC=120°. AB=BC=a, AC=b.
过B作BD⊥AC于点D,
则AD=DC= b.
在Rt△ABD中,∠BAC=30°,
∴BD= AB=3mm.
∴b=2AD=6 mm.
即扳手张开的开口b至少要6 mm.
A
C
B D
当堂训练
课堂小结
肆
正多边形
正多边形的定义与对称性
正多边形的有
关概念及性质
①正多边形的内角和=
②中心角=
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
课堂小结
课后作业
基础题:1.课后习题 24.3的复习巩固
提高题:2.请学有余力的同学做P108”综合运用”
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
