25.2 用列举法求概率 第2课时 画树状图求概率 课件(共24张PPT)
文档属性
| 名称 | 25.2 用列举法求概率 第2课时 画树状图求概率 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 17:35:41 | ||
图片预览







文档简介
(共24张PPT)
第二十五章 概率初步
第2课时 画树状图求概率
25.2 用列举法求概率
学习目标
1.进一步理解等可能事件概率的意义.
2.学习运用树形图计算事件的概率.
3.进一步学习分类思想方法,掌握有关数学技能.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
抛掷一枚均匀的硬币,出现正面向上的概率是多少?
P(正面向上) =
同时抛掷两枚均匀的硬币,出现同时正面向上的概率是多少?
可能出现的结果有(正,正)(正,反)(反,正)(反,反),
P(同时正面向上)=
还有别的方法求此问的概率吗?
新课导入
讲授新知
贰
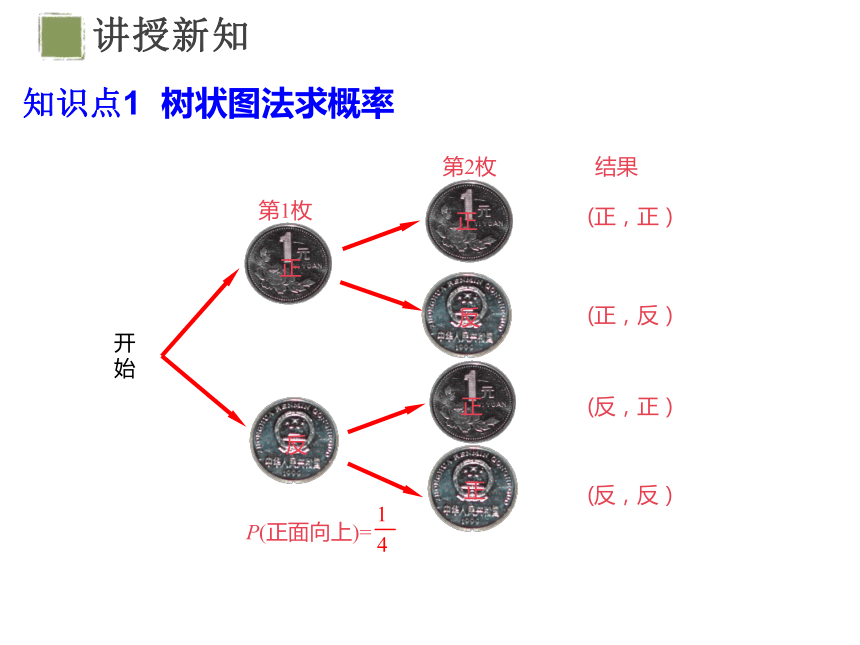
开始
第2枚
第1枚
正
反
正
反
正
正
结果
(反,反)
(正,正)
(正,反)
(反,正)
P(正面向上)=
知识点1 树状图法求概率
讲授新知
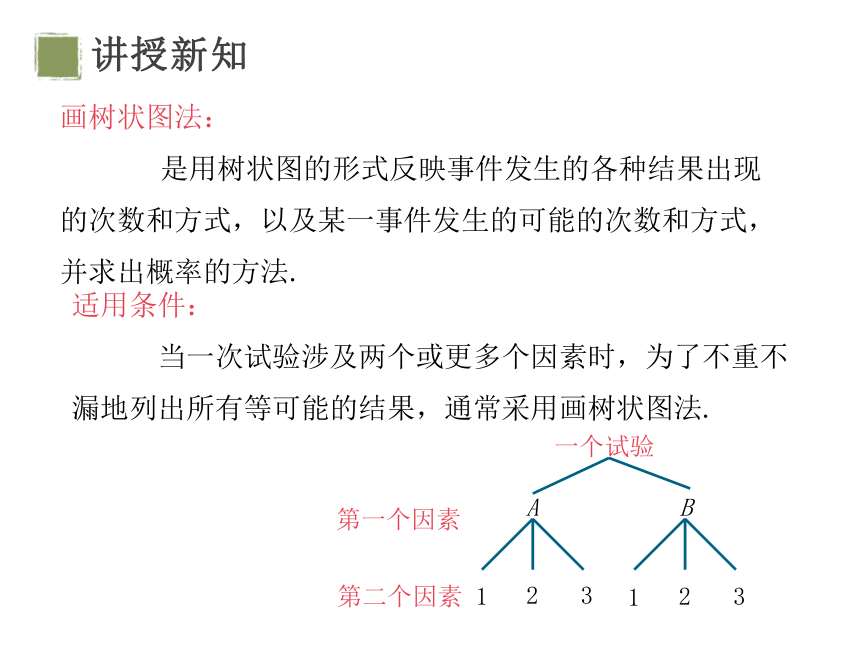
适用条件:
当一次试验涉及两个或更多个因素时,为了不重不漏地列出所有等可能的结果,通常采用画树状图法.
一个试验
第一个因素
第二个因素
A
B
1
2
3
1
2
3
画树状图法:
是用树状图的形式反映事件发生的各种结果出现的次数和方式,以及某一事件发生的可能的次数和方式,并求出概率的方法.
讲授新知
画树状图求概率的基本步骤:
(1) 将第一步可能出现的 a 种等可能的结果写在第一层;
(2) 若第二步有 b 种等可能的结果,则在第一层的每个结果下画出 b 个分支,将这 b 种结果写在第二层,以此类推,画出第三层;
(3) 根据树状图求出所关注事件包含的结果数及所有等可能的结果数,再利用概率公式求解.
讲授新知
例 甲口袋中有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(1) 取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2) 取出的3个小球上全是辅音字母的概率是多少?
分析:当一次试验是从三个口袋中取球时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
范例应用
解:根据题意,可以画出如下的树状图:
由树状图可以看出,所有可能出现的结果共有12种,即ACH,ACI,ADH,ADI,AEH,AEI,BCH,BCI,BDH,BDI,BEH,BEI,
这些结果出现的可能性相等.
范例应用
范例应用
总结归纳
1.用列举法求事件的概率包括直接列举法、列表法和画树状图法,用列举法求概率时,各种结果出现的可能性必须相同,必须列举出所有可能的结果,不能重复也不能遗漏.
2.当试验包含两步时,用列表法比较方便,当然此时也可以用画树状图法;当试验包含三步或三步以上时,不能用列表法,用画树状图法比较方便.
3.树状图中,从左到右(或从上往下),每一条路径都表示一种可能的结果,并且每种结果出现的可能性相同.
练一练
经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两车向右,一车向左;
(3)至少两车向左.
范例应用
第一辆
左
右
左
右
左直右
第二辆
第三辆
直
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
共有27种行驶方向
(2)P(两车向右,一车向左)= ;
(3) P(至少两车向左)=
范例应用
当堂训练
叁
2.有一箱子装有3张分别标示4、5、6的号码牌,已知小武以每次取一张且取后不放回的方式,先后取出2张牌,组成一个二位数,取出第1张牌的号码为十位数,第2张牌的号码为个位数,若先后取出2张牌组成二位数的每一种结果发生的机会都相同,则组成的二位数为6的倍数的概率为( )
1.学校新开设了航模、彩绘、泥塑三个社团,如果征征、舟舟两名同学每人随机选择参加其中一个社团,那么征征和舟舟选到同一社团的概率是( )
B
D
A. B. C. D.
当堂训练
3.从1、2、-3三个数中,随机抽取两个数相乘,积是负数的概率是 .
当堂训练
4.a、b、c、d四本不同的书放入一个书包,至少放一本,最多放2本,共有 种不同的放法.
10
5.在一个不透明的布袋中装有2个白球和n个黄球,它们除颜色外,其余均相同,若从中随机摸出一个球,摸到黄球的概率为 ,则n= .
8
课堂小结
肆
课堂小结
树状图
步骤
用法
是一种解决试验有多步(或涉及多个因素)的好方法.
注意
弄清试验涉及试验因素个数或试验步骤分几步;
在摸球试验一定要弄清“放回”还是“不放回”.
关键要弄清楚每一步有几种结果;
在树状图下面对应写着所有可能的结果;
利用概率公式进行计算.
课后作业
基础题:1.课后习题P140T 4--6 。
提高题:2.请学有余力的同学做拓广探索T7、T8.
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二十五章 概率初步
第2课时 画树状图求概率
25.2 用列举法求概率
学习目标
1.进一步理解等可能事件概率的意义.
2.学习运用树形图计算事件的概率.
3.进一步学习分类思想方法,掌握有关数学技能.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
抛掷一枚均匀的硬币,出现正面向上的概率是多少?
P(正面向上) =
同时抛掷两枚均匀的硬币,出现同时正面向上的概率是多少?
可能出现的结果有(正,正)(正,反)(反,正)(反,反),
P(同时正面向上)=
还有别的方法求此问的概率吗?
新课导入
讲授新知
贰
开始
第2枚
第1枚
正
反
正
反
正
正
结果
(反,反)
(正,正)
(正,反)
(反,正)
P(正面向上)=
知识点1 树状图法求概率
讲授新知
适用条件:
当一次试验涉及两个或更多个因素时,为了不重不漏地列出所有等可能的结果,通常采用画树状图法.
一个试验
第一个因素
第二个因素
A
B
1
2
3
1
2
3
画树状图法:
是用树状图的形式反映事件发生的各种结果出现的次数和方式,以及某一事件发生的可能的次数和方式,并求出概率的方法.
讲授新知
画树状图求概率的基本步骤:
(1) 将第一步可能出现的 a 种等可能的结果写在第一层;
(2) 若第二步有 b 种等可能的结果,则在第一层的每个结果下画出 b 个分支,将这 b 种结果写在第二层,以此类推,画出第三层;
(3) 根据树状图求出所关注事件包含的结果数及所有等可能的结果数,再利用概率公式求解.
讲授新知
例 甲口袋中有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(1) 取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2) 取出的3个小球上全是辅音字母的概率是多少?
分析:当一次试验是从三个口袋中取球时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
范例应用
解:根据题意,可以画出如下的树状图:
由树状图可以看出,所有可能出现的结果共有12种,即ACH,ACI,ADH,ADI,AEH,AEI,BCH,BCI,BDH,BDI,BEH,BEI,
这些结果出现的可能性相等.
范例应用
范例应用
总结归纳
1.用列举法求事件的概率包括直接列举法、列表法和画树状图法,用列举法求概率时,各种结果出现的可能性必须相同,必须列举出所有可能的结果,不能重复也不能遗漏.
2.当试验包含两步时,用列表法比较方便,当然此时也可以用画树状图法;当试验包含三步或三步以上时,不能用列表法,用画树状图法比较方便.
3.树状图中,从左到右(或从上往下),每一条路径都表示一种可能的结果,并且每种结果出现的可能性相同.
练一练
经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两车向右,一车向左;
(3)至少两车向左.
范例应用
第一辆
左
右
左
右
左直右
第二辆
第三辆
直
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
共有27种行驶方向
(2)P(两车向右,一车向左)= ;
(3) P(至少两车向左)=
范例应用
当堂训练
叁
2.有一箱子装有3张分别标示4、5、6的号码牌,已知小武以每次取一张且取后不放回的方式,先后取出2张牌,组成一个二位数,取出第1张牌的号码为十位数,第2张牌的号码为个位数,若先后取出2张牌组成二位数的每一种结果发生的机会都相同,则组成的二位数为6的倍数的概率为( )
1.学校新开设了航模、彩绘、泥塑三个社团,如果征征、舟舟两名同学每人随机选择参加其中一个社团,那么征征和舟舟选到同一社团的概率是( )
B
D
A. B. C. D.
当堂训练
3.从1、2、-3三个数中,随机抽取两个数相乘,积是负数的概率是 .
当堂训练
4.a、b、c、d四本不同的书放入一个书包,至少放一本,最多放2本,共有 种不同的放法.
10
5.在一个不透明的布袋中装有2个白球和n个黄球,它们除颜色外,其余均相同,若从中随机摸出一个球,摸到黄球的概率为 ,则n= .
8
课堂小结
肆
课堂小结
树状图
步骤
用法
是一种解决试验有多步(或涉及多个因素)的好方法.
注意
弄清试验涉及试验因素个数或试验步骤分几步;
在摸球试验一定要弄清“放回”还是“不放回”.
关键要弄清楚每一步有几种结果;
在树状图下面对应写着所有可能的结果;
利用概率公式进行计算.
课后作业
基础题:1.课后习题P140T 4--6 。
提高题:2.请学有余力的同学做拓广探索T7、T8.
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
