25.3 用频率估计概率 课件(共23张PPT)
文档属性
| 名称 | 25.3 用频率估计概率 课件(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
第二十五章 概率初步
25.3 用频率估计概率
学习目标
1.用频率估计概率并解决实际问题. (难点)
2.通过概率计算进一步比较概率与频率之间的关系.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
在学完用列举法求随机事件发生的概率这节内容后,小明同学提出一个问题.他抛掷一枚硬币10次,其正面朝上的次数为5次,是否可以说明“正面向上”这一事件发生的概率为0.5?
用列举法可以求一些事件的概率.实际上,我们还可以利用多次重复试验,通过统计试验结果估计概率.
新课导入
讲授新知
贰
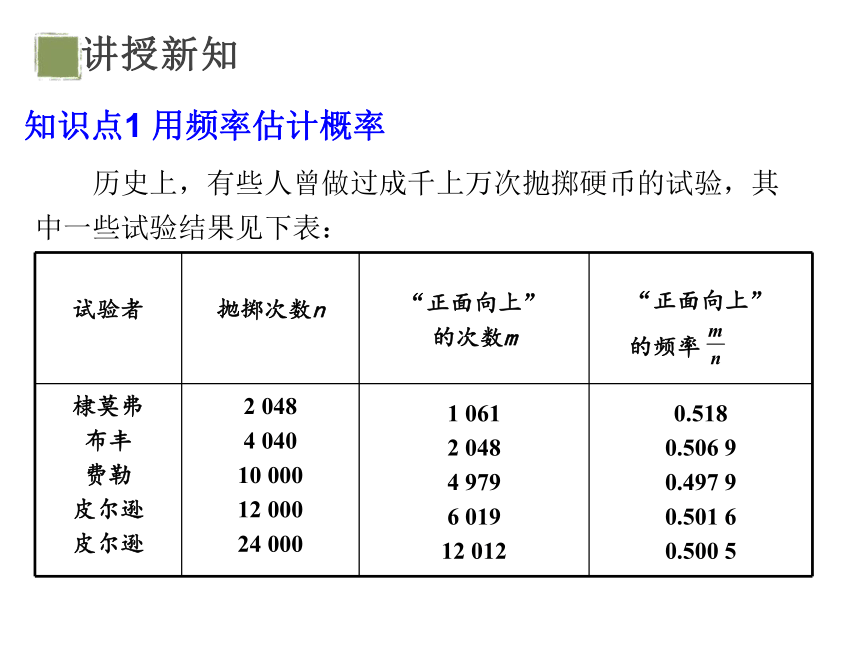
历史上,有些人曾做过成千上万次抛掷硬币的试验,其中一些试验结果见下表:
试验者 抛掷次数n “正面向上”
的次数m “正面向上”
的频率
棣莫弗 布丰 费勒 皮尔逊 皮尔逊 2 048 4 040 10 000 12 000 24 000 1 061 2 048 4 979 6 019 12 012 0.518
0.506 9
0.497 9
0.501 6
0.500 5
知识点1 用频率估计概率
讲授新知
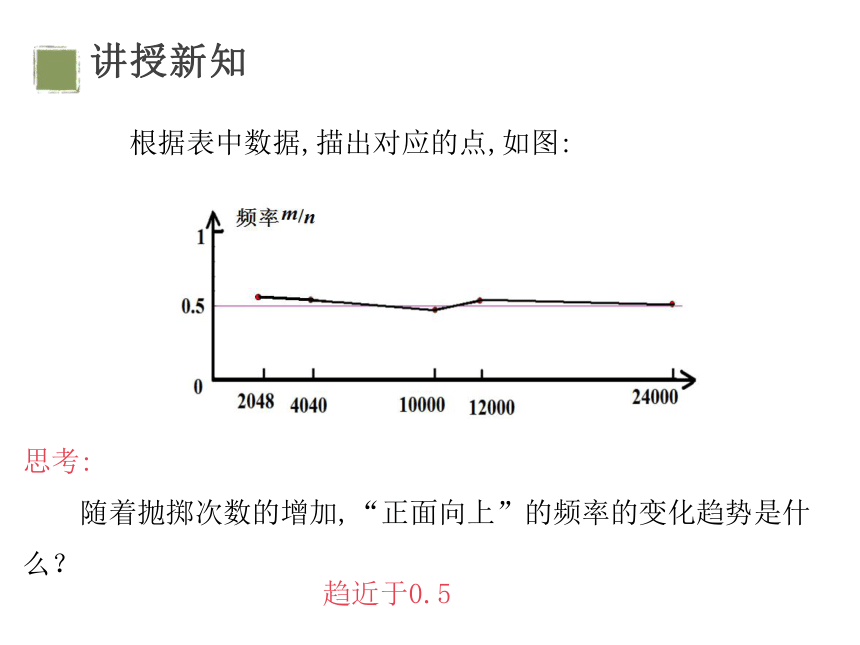
根据表中数据,描出对应的点,如图:
思考:
随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么?
趋近于0.5
讲授新知
对一般的随机事件在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性,因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
为什么要用频率估计概率?虽然之前我们学过用列举法确切地计算出随机事件的概率,但由于列举法受各种结果出现的可能性相等的限制,有些事件的概率并不能用列举法求出.例如:抛掷一枚图钉,估计“钉尖朝上”的概率,这时我们就可以通过大量重复试验估计它们的概率.
讲授新知
例1 某林业部门要考察某种幼树在一定条件下的
移植成活率,应采用什么具体做法
是实际问题中的一种概率,可理解为成活的概率.
观察在各次试验中得到的幼树成活的频率,谈谈你的看法.
范例应用
移植总数(n) 成活数(m) 成活的频率
10 8 0.8
50 47
270 235 0.870
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
0.94
0.923
0.883
0.905
0.897
由上表可以发现,幼树移植成活的频率在 左右摆动,并且随着移植棵数越来越大,这种规律愈加明显.
所以估计幼树移植成活的概率为 .
0.9
0.9
1 林业部门种植了该幼树1000棵,估计能成活_____棵.
2 我们学校需种植这样的树苗500棵来绿化校园,则 至少向林业部门购买约_______棵.
900
560
范例应用
1.频率与概率的关系:在大量重复试验中,如果事件A发生的频率 稳定于某个常数b,则该事件发生的概率P(A)= ____.
b
频率 概率
区别 试验值或使用时的统计值 理论值
与试验次数的 变化有关 与试验次数的
变化无关
与试验人、试验时间、 试验地点有关 与试验人、试验时间、试验地点无关
联系 试验次数越多,频率越趋向于概率 知识点2 频率与概率的关系
讲授新知
例2 某水果公司以2元/千克的成本新进了10000千克柑橘,如果公司希望这些柑橘能够获得利润5000元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
分析 根据上表估计柑橘损坏的概率为0.1,则柑橘完好的概率为0.9.
范例应用
解:根据估计的概率可以知道,在10000千克柑橘中完好柑橘的质量为10000×0.9=9000千克,完好柑橘的实际成本为
设每千克柑橘的销价为x元,则应有
(x-2.22)×9000=5000,
解得 x≈2.8.
因此,出售柑橘时每千克大约定价为2.8元可获利润5000元.
范例应用
当堂训练
叁
1.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
2.在一个不透明的口袋里,装有仅颜色不同的黑球、白球若干个,某小组做摸球试验:将球搅匀后从中随机摸出一个,记下颜色,再放入袋中,不断重复,下表是活动中的一组数据,则摸到白球的概率约是( )
A.0.4 B.0.5 C.0.6 D.0.7
C
当堂训练
4.某射击运动员在同一条件下的射击成绩记录如下:
(1)计算表中相应的“射中9环以上”的频率(精确到0.01);
(2)这些频率具有什么样的稳定性?
(3)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1)
射击次数 20 40 100 200 400 1000
“射中九环以上”的次数 15 33 78 158 321 801
“射中九环以上”的频率
稳定在0.8附近
0.8
0.75
0.83
0.78
0.79
0.80
0.80
3.一个口袋中放有20个球,其中红球6个,白球和黑球若干个,每个球除了颜色外没有任何区别,小王通过大量重复试验(每次取一个球,放回搅匀后再取)发现,取出黑球的频率稳定在0.25左右,请你估计袋中黑球的个数为 .
5
当堂训练
课堂小结
肆
频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概率
但概率与频率无关
课堂小结
课后作业
基础题:1.课后习题P147T 3--4--5 。
提高题:2.请学有余力的同学做拓广探索T6.
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二十五章 概率初步
25.3 用频率估计概率
学习目标
1.用频率估计概率并解决实际问题. (难点)
2.通过概率计算进一步比较概率与频率之间的关系.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
在学完用列举法求随机事件发生的概率这节内容后,小明同学提出一个问题.他抛掷一枚硬币10次,其正面朝上的次数为5次,是否可以说明“正面向上”这一事件发生的概率为0.5?
用列举法可以求一些事件的概率.实际上,我们还可以利用多次重复试验,通过统计试验结果估计概率.
新课导入
讲授新知
贰
历史上,有些人曾做过成千上万次抛掷硬币的试验,其中一些试验结果见下表:
试验者 抛掷次数n “正面向上”
的次数m “正面向上”
的频率
棣莫弗 布丰 费勒 皮尔逊 皮尔逊 2 048 4 040 10 000 12 000 24 000 1 061 2 048 4 979 6 019 12 012 0.518
0.506 9
0.497 9
0.501 6
0.500 5
知识点1 用频率估计概率
讲授新知
根据表中数据,描出对应的点,如图:
思考:
随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么?
趋近于0.5
讲授新知
对一般的随机事件在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性,因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
为什么要用频率估计概率?虽然之前我们学过用列举法确切地计算出随机事件的概率,但由于列举法受各种结果出现的可能性相等的限制,有些事件的概率并不能用列举法求出.例如:抛掷一枚图钉,估计“钉尖朝上”的概率,这时我们就可以通过大量重复试验估计它们的概率.
讲授新知
例1 某林业部门要考察某种幼树在一定条件下的
移植成活率,应采用什么具体做法
是实际问题中的一种概率,可理解为成活的概率.
观察在各次试验中得到的幼树成活的频率,谈谈你的看法.
范例应用
移植总数(n) 成活数(m) 成活的频率
10 8 0.8
50 47
270 235 0.870
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
0.94
0.923
0.883
0.905
0.897
由上表可以发现,幼树移植成活的频率在 左右摆动,并且随着移植棵数越来越大,这种规律愈加明显.
所以估计幼树移植成活的概率为 .
0.9
0.9
1 林业部门种植了该幼树1000棵,估计能成活_____棵.
2 我们学校需种植这样的树苗500棵来绿化校园,则 至少向林业部门购买约_______棵.
900
560
范例应用
1.频率与概率的关系:在大量重复试验中,如果事件A发生的频率 稳定于某个常数b,则该事件发生的概率P(A)= ____.
b
频率 概率
区别 试验值或使用时的统计值 理论值
与试验次数的 变化有关 与试验次数的
变化无关
与试验人、试验时间、 试验地点有关 与试验人、试验时间、试验地点无关
联系 试验次数越多,频率越趋向于概率 知识点2 频率与概率的关系
讲授新知
例2 某水果公司以2元/千克的成本新进了10000千克柑橘,如果公司希望这些柑橘能够获得利润5000元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
分析 根据上表估计柑橘损坏的概率为0.1,则柑橘完好的概率为0.9.
范例应用
解:根据估计的概率可以知道,在10000千克柑橘中完好柑橘的质量为10000×0.9=9000千克,完好柑橘的实际成本为
设每千克柑橘的销价为x元,则应有
(x-2.22)×9000=5000,
解得 x≈2.8.
因此,出售柑橘时每千克大约定价为2.8元可获利润5000元.
范例应用
当堂训练
叁
1.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
2.在一个不透明的口袋里,装有仅颜色不同的黑球、白球若干个,某小组做摸球试验:将球搅匀后从中随机摸出一个,记下颜色,再放入袋中,不断重复,下表是活动中的一组数据,则摸到白球的概率约是( )
A.0.4 B.0.5 C.0.6 D.0.7
C
当堂训练
4.某射击运动员在同一条件下的射击成绩记录如下:
(1)计算表中相应的“射中9环以上”的频率(精确到0.01);
(2)这些频率具有什么样的稳定性?
(3)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1)
射击次数 20 40 100 200 400 1000
“射中九环以上”的次数 15 33 78 158 321 801
“射中九环以上”的频率
稳定在0.8附近
0.8
0.75
0.83
0.78
0.79
0.80
0.80
3.一个口袋中放有20个球,其中红球6个,白球和黑球若干个,每个球除了颜色外没有任何区别,小王通过大量重复试验(每次取一个球,放回搅匀后再取)发现,取出黑球的频率稳定在0.25左右,请你估计袋中黑球的个数为 .
5
当堂训练
课堂小结
肆
频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概率
但概率与频率无关
课堂小结
课后作业
基础题:1.课后习题P147T 3--4--5 。
提高题:2.请学有余力的同学做拓广探索T6.
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
