3.4 第3课时 收费及其他问题 课件(共30张PPT)
文档属性
| 名称 | 3.4 第3课时 收费及其他问题 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 17:37:38 | ||
图片预览








文档简介
(共30张PPT)
第三章 一元一次方程
第3课时 收费及其他问题
3.4 实际问题与一元一次方程
学习目标
学习目标
1.体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点对“电话计费问题”进行整体分析,从而得出整体选择方案.
2.进一步深化对数学建模方法的体验,增强应用方程模型解决问题的意识和能力.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
在科技迅猛发展的今天,移动电话成为了人们生活中非常普及的通讯工具,选择经济实惠的资费方式成为了我们所关心而且具有实际意义的问题,你知道你的家人都选择了哪种资费吗?
讲授新知
贰
讲授新知
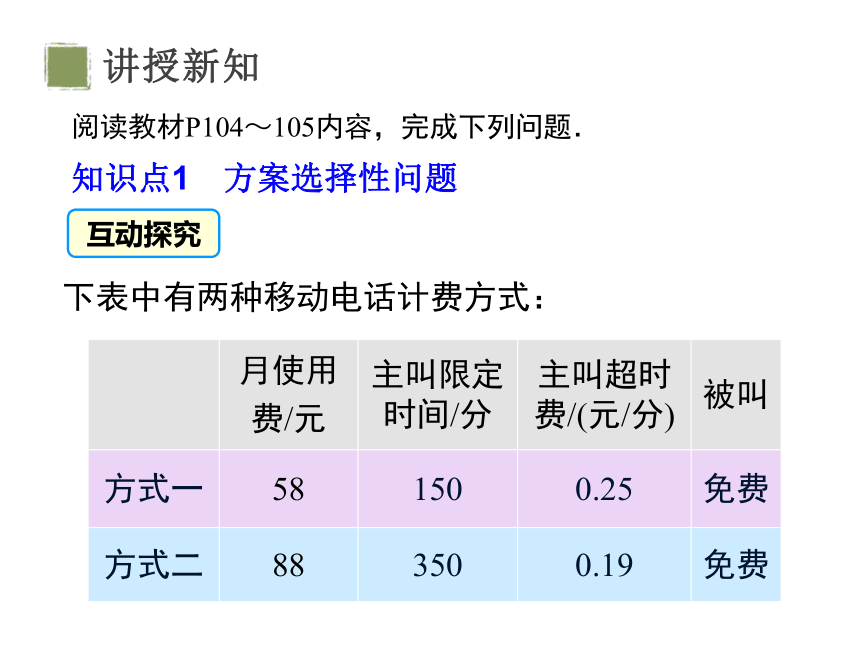
阅读教材P104~105内容,完成下列问题.
知识点1 方案选择性问题
互动探究
下表中有两种移动电话计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
讲授新知
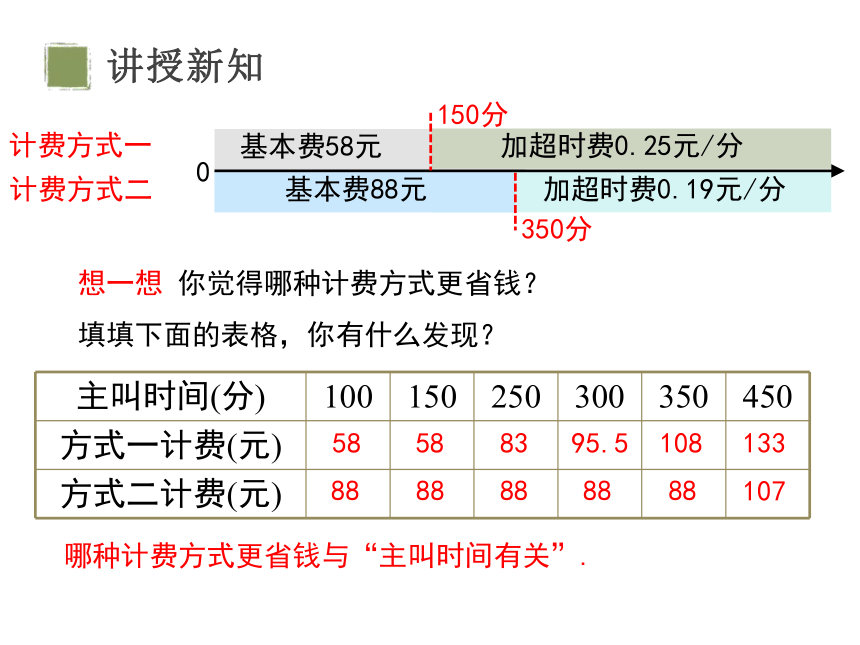
想一想 你觉得哪种计费方式更省钱?
填填下面的表格,你有什么发现?
主叫时间(分) 100 150 250 300 350 450
方式一计费(元)
方式二计费(元)
58
58
83
95.5
108
133
88
88
88
88
88
107
计费方式一
0
加超时费0.19元/分
基本费88元
基本费58元
加超时费0.25元/分
150分
350分
计费方式二
哪种计费方式更省钱与“主叫时间有关”.
讲授新知
考虑 t 的取值时,两个主叫限定时间 150 min和 350 min是不同时间范围的划分点.
计费时首先要看主叫是否超过限定时间,主叫不超过限定时间,月使用费一定;
主叫超过限定时间,超时部分加收超时费.
问题1 设一个月内移动电话主叫为 t min (t是正整数),列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
讲授新知
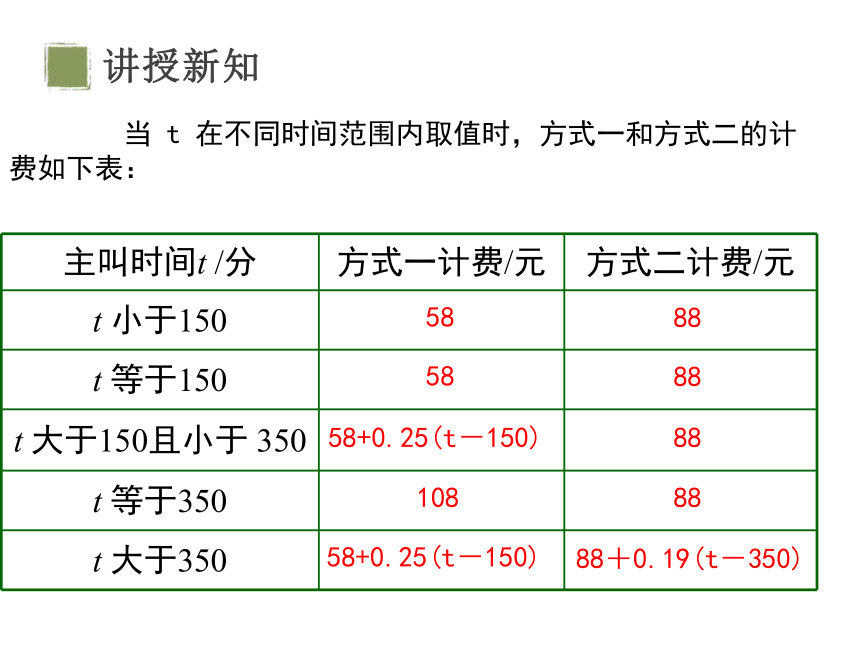
当 t 在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
58
88
58
88
58+0.25(t-150)
88
88
108
58+0.25(t-150)
88+0.19(t-350)
讲授新知
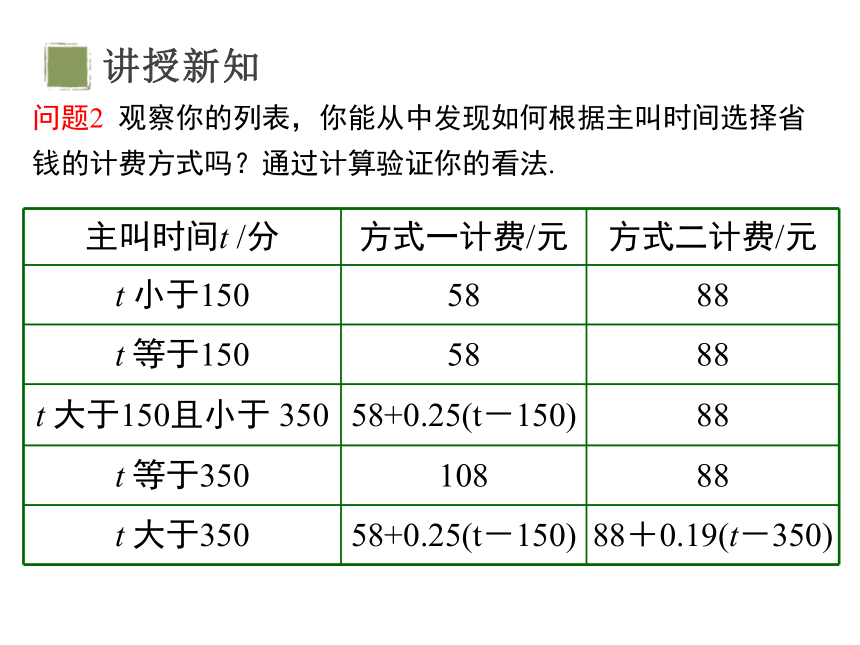
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
问题2 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
讲授新知
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
①当t ≤150时,方式一计费少(58元);
(1) 比较下列表格的第2、3行,你能得出什么结论?
<
<
讲授新知
主叫时间t /分 方式一计费/元 方式二计费/元
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
(2) 比较下列表格的第2、4行,你能得出什么结论?
>
<
当t 大于150且小于 350时,存在某一个值,使得两种方式计费相等.
依题意 ,得58+0.25(t-150) = 88,
解得 t =270.
讲授新知
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于350 58+0.25(t-150) 88+0.19(t-350)
解析:当t>350分时,方式一的计费其实就是在108元的基础上,加上超过350分部分的超时费[0.25(t-350)].
(3) 当t >350分时,两种计费方式哪种更合算呢?
当t >350时,
方式一: 58+0.25(t-150)= 108+0.25(t-350),
方式二: 88+0.19(t-350),
所以,当t >350分时,方式二计费少.
讲授新知
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
108
88
58
88
( t 是正整数)
t /分
88
88
270
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱;
时,方式一、方式二均可.
t 小于 270
t 大于 270
t 等于 270
讲授新课
知识点2 分段计费问题
互动探究
为了鼓励居民节约用水,某市自来水公司按如下方式对每户月用水量进行计费:当用水量不超过10吨时,每吨的收费标准相同;当用水量超过10吨时,超出10吨的部分每吨收费标准也相同.下表是小明家1-4月份用水量和交费情况:
月份 1 2 3 4
用水量(吨) 8 10 12 15
费用(元) 16 20 26 35
讲授新课
请根据表格中提供的信息,回答以下问题:
(1)若小明家5月份用水量为20吨,则应缴水费多少元?
(2)若小明家6月份交纳水费29元,则小明家6月份用水多少吨?
【分析】
(1)根据1月份的条件,当用水量不超过10吨时,每吨的收费2元.根据3月份的条件,用水12吨,其中10吨应交20元,则超过的2吨收费6元,则超出10吨的部分每吨收费3元.则用水20吨应缴水费就可以算出;
(2)中存在的相等关系是:10吨的费用20元+超过部分的费用=29元.
讲授新课
解:(1)从表中可以看出规定吨数位不超过10吨,10吨以内,每吨2元,超过10吨的部分每吨3元,
小明家5月份的水费是:10×2+(20-10)×3=50元;
(2)设小明家6月份用水x吨,29>10×2,所以x>10.
所以,10×2+(x-10)×3=29,
解得:x=13.
小明家6月份用水13吨.
讲授新课
【练习】
参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:
住院医疗费(元) 报销率(%)
不超过500元的部分 0
500~1000元的部分 60
1000~3000元的部分 80
… …
某人住院治疗得到保险公司的报销金额是1100元,则此人住院的医疗费是( )
A.1000元 B.1500元 C.1625元 D.2000元
D
当堂训练
叁
当堂训练
1.下表为某市居民每月用水收费标准.(单位:元/m3).
用水量 单价
x≤22 a
剩余部分 a+1.1
(1)某用户用水10立方米,共交水费23元,求a的值;
(2)在(1)的前提下,该用户5月份交水费71元,请问该用户用水多少立方米?
当堂训练
解:(1)由题意可得:10a=23,
解得:a=2.3,
答:a的值为2.3;
(2)设用户水量为x立方米,
∵用水22立方米时,水费为:22×2.3=50.6<71,
∴x>22,
∴22×2.3+(x-22)×(2.3+1.1)=71,
解得:x=28,
答:该用户用水28立方米.
当堂训练
2.某班打算买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)当购买乒乓球15盒时,去哪家店购买比较优惠?
(2)当购买乒乓球多少盒时,两家店的付款一样多?
当堂训练
解:(1)甲:30×5+5×(15-5)=200(元)
乙:(30×5+5×15)×0.9=202.5(元)
因为200<202.5,
所以当购买乒乓球15盒时,去甲商店购买比较优惠,
答:当购买乒乓球15盒时,去甲商店购买比较优惠.
(2)设购买x 盒乒乓球时,两家店的付款一样多,
根据题意得:
30×5+5(x-5)=(30×5+5x)×0.9,
解得:x=20,
答:当购买乒乓球20盒时,两家店的付款一样多.
课堂小结
肆
课堂小结
1. 解决电话计费问题需要明确“哪种计费方式更省
钱”与“主叫时间”有关.
2. 此类问题的关键是能够根据已知条件找到合适
的分段点,然后建立方程模型分类讨论,从而
得出整体选择方案.
课后作业
基础题:1.课后练习题 第2,3题。
提高题:2.课后练习题 第10题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第三章 一元一次方程
第3课时 收费及其他问题
3.4 实际问题与一元一次方程
学习目标
学习目标
1.体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点对“电话计费问题”进行整体分析,从而得出整体选择方案.
2.进一步深化对数学建模方法的体验,增强应用方程模型解决问题的意识和能力.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
在科技迅猛发展的今天,移动电话成为了人们生活中非常普及的通讯工具,选择经济实惠的资费方式成为了我们所关心而且具有实际意义的问题,你知道你的家人都选择了哪种资费吗?
讲授新知
贰
讲授新知
阅读教材P104~105内容,完成下列问题.
知识点1 方案选择性问题
互动探究
下表中有两种移动电话计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
讲授新知
想一想 你觉得哪种计费方式更省钱?
填填下面的表格,你有什么发现?
主叫时间(分) 100 150 250 300 350 450
方式一计费(元)
方式二计费(元)
58
58
83
95.5
108
133
88
88
88
88
88
107
计费方式一
0
加超时费0.19元/分
基本费88元
基本费58元
加超时费0.25元/分
150分
350分
计费方式二
哪种计费方式更省钱与“主叫时间有关”.
讲授新知
考虑 t 的取值时,两个主叫限定时间 150 min和 350 min是不同时间范围的划分点.
计费时首先要看主叫是否超过限定时间,主叫不超过限定时间,月使用费一定;
主叫超过限定时间,超时部分加收超时费.
问题1 设一个月内移动电话主叫为 t min (t是正整数),列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
讲授新知
当 t 在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
58
88
58
88
58+0.25(t-150)
88
88
108
58+0.25(t-150)
88+0.19(t-350)
讲授新知
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
问题2 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
讲授新知
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
①当t ≤150时,方式一计费少(58元);
(1) 比较下列表格的第2、3行,你能得出什么结论?
<
<
讲授新知
主叫时间t /分 方式一计费/元 方式二计费/元
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
(2) 比较下列表格的第2、4行,你能得出什么结论?
>
<
当t 大于150且小于 350时,存在某一个值,使得两种方式计费相等.
依题意 ,得58+0.25(t-150) = 88,
解得 t =270.
讲授新知
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于350 58+0.25(t-150) 88+0.19(t-350)
解析:当t>350分时,方式一的计费其实就是在108元的基础上,加上超过350分部分的超时费[0.25(t-350)].
(3) 当t >350分时,两种计费方式哪种更合算呢?
当t >350时,
方式一: 58+0.25(t-150)= 108+0.25(t-350),
方式二: 88+0.19(t-350),
所以,当t >350分时,方式二计费少.
讲授新知
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
108
88
58
88
( t 是正整数)
t /分
88
88
270
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱;
时,方式一、方式二均可.
t 小于 270
t 大于 270
t 等于 270
讲授新课
知识点2 分段计费问题
互动探究
为了鼓励居民节约用水,某市自来水公司按如下方式对每户月用水量进行计费:当用水量不超过10吨时,每吨的收费标准相同;当用水量超过10吨时,超出10吨的部分每吨收费标准也相同.下表是小明家1-4月份用水量和交费情况:
月份 1 2 3 4
用水量(吨) 8 10 12 15
费用(元) 16 20 26 35
讲授新课
请根据表格中提供的信息,回答以下问题:
(1)若小明家5月份用水量为20吨,则应缴水费多少元?
(2)若小明家6月份交纳水费29元,则小明家6月份用水多少吨?
【分析】
(1)根据1月份的条件,当用水量不超过10吨时,每吨的收费2元.根据3月份的条件,用水12吨,其中10吨应交20元,则超过的2吨收费6元,则超出10吨的部分每吨收费3元.则用水20吨应缴水费就可以算出;
(2)中存在的相等关系是:10吨的费用20元+超过部分的费用=29元.
讲授新课
解:(1)从表中可以看出规定吨数位不超过10吨,10吨以内,每吨2元,超过10吨的部分每吨3元,
小明家5月份的水费是:10×2+(20-10)×3=50元;
(2)设小明家6月份用水x吨,29>10×2,所以x>10.
所以,10×2+(x-10)×3=29,
解得:x=13.
小明家6月份用水13吨.
讲授新课
【练习】
参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:
住院医疗费(元) 报销率(%)
不超过500元的部分 0
500~1000元的部分 60
1000~3000元的部分 80
… …
某人住院治疗得到保险公司的报销金额是1100元,则此人住院的医疗费是( )
A.1000元 B.1500元 C.1625元 D.2000元
D
当堂训练
叁
当堂训练
1.下表为某市居民每月用水收费标准.(单位:元/m3).
用水量 单价
x≤22 a
剩余部分 a+1.1
(1)某用户用水10立方米,共交水费23元,求a的值;
(2)在(1)的前提下,该用户5月份交水费71元,请问该用户用水多少立方米?
当堂训练
解:(1)由题意可得:10a=23,
解得:a=2.3,
答:a的值为2.3;
(2)设用户水量为x立方米,
∵用水22立方米时,水费为:22×2.3=50.6<71,
∴x>22,
∴22×2.3+(x-22)×(2.3+1.1)=71,
解得:x=28,
答:该用户用水28立方米.
当堂训练
2.某班打算买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)当购买乒乓球15盒时,去哪家店购买比较优惠?
(2)当购买乒乓球多少盒时,两家店的付款一样多?
当堂训练
解:(1)甲:30×5+5×(15-5)=200(元)
乙:(30×5+5×15)×0.9=202.5(元)
因为200<202.5,
所以当购买乒乓球15盒时,去甲商店购买比较优惠,
答:当购买乒乓球15盒时,去甲商店购买比较优惠.
(2)设购买x 盒乒乓球时,两家店的付款一样多,
根据题意得:
30×5+5(x-5)=(30×5+5x)×0.9,
解得:x=20,
答:当购买乒乓球20盒时,两家店的付款一样多.
课堂小结
肆
课堂小结
1. 解决电话计费问题需要明确“哪种计费方式更省
钱”与“主叫时间”有关.
2. 此类问题的关键是能够根据已知条件找到合适
的分段点,然后建立方程模型分类讨论,从而
得出整体选择方案.
课后作业
基础题:1.课后练习题 第2,3题。
提高题:2.课后练习题 第10题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
