第8单元数学广角-数与形常考易错练习卷(单元测试)-小学数学六年级上册人教版(含解析)
文档属性
| 名称 | 第8单元数学广角-数与形常考易错练习卷(单元测试)-小学数学六年级上册人教版(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 09:21:18 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第8单元数学广角-数与形练习卷-小学数学六年级上册人教版
一、选择题
1.下图能够大概描述汽车由静止开始发动,加速到一定速度匀速行驶一段距离后减速上坡,再加速下坡,然后逐渐减速到匀速行驶的过程是( )。www-2-1-cnjy-com
A. B.
C. D.
2.如图,观察下列正三角形的三个顶点所标的数字规律,那么2008这个数在第( )个三角形的( )顶点处。( )
A.669;上 B.669;左下 C.670;右下 D.670;上
3.像这样摆下去,n个梯形需要的小棒根数是( )根。
A. B. C.
4.按规律摆六边形,如果摆n个六边形,需要( )根小棒。
A.6n B. C.
5.如图所示,用黑白两种颜色的正五边形地砖按下图所示的规律,拼成若干个蝴蝶图案,则第7个蝴蝶图案中白色地砖有( )。
A.35块 B.27块 C.22块 D.7块
6.下列图形都是由同样大小的黑色圆点按照一定规律所组成的,其中第1个图形中一共有5个黑色圆点,第2个图形中一共有14个黑色圆点,第3个图形中一共有27个黑色圆点……按此规律排列下去,第6个图形中有( )个黑色圆点。
A.65 B.91 C.78 D.90
7.如图是“杨辉三角”,根据各数之间的关系,第6行中所有数的和是( )。
A.32 B.22 C.20
8.观察下边图形,按此规律,第⑩个图中○的个数有( )个。
A.55 B.40 C.36 D.10
二、填空题
9.+++++1+2+4+8=( )。
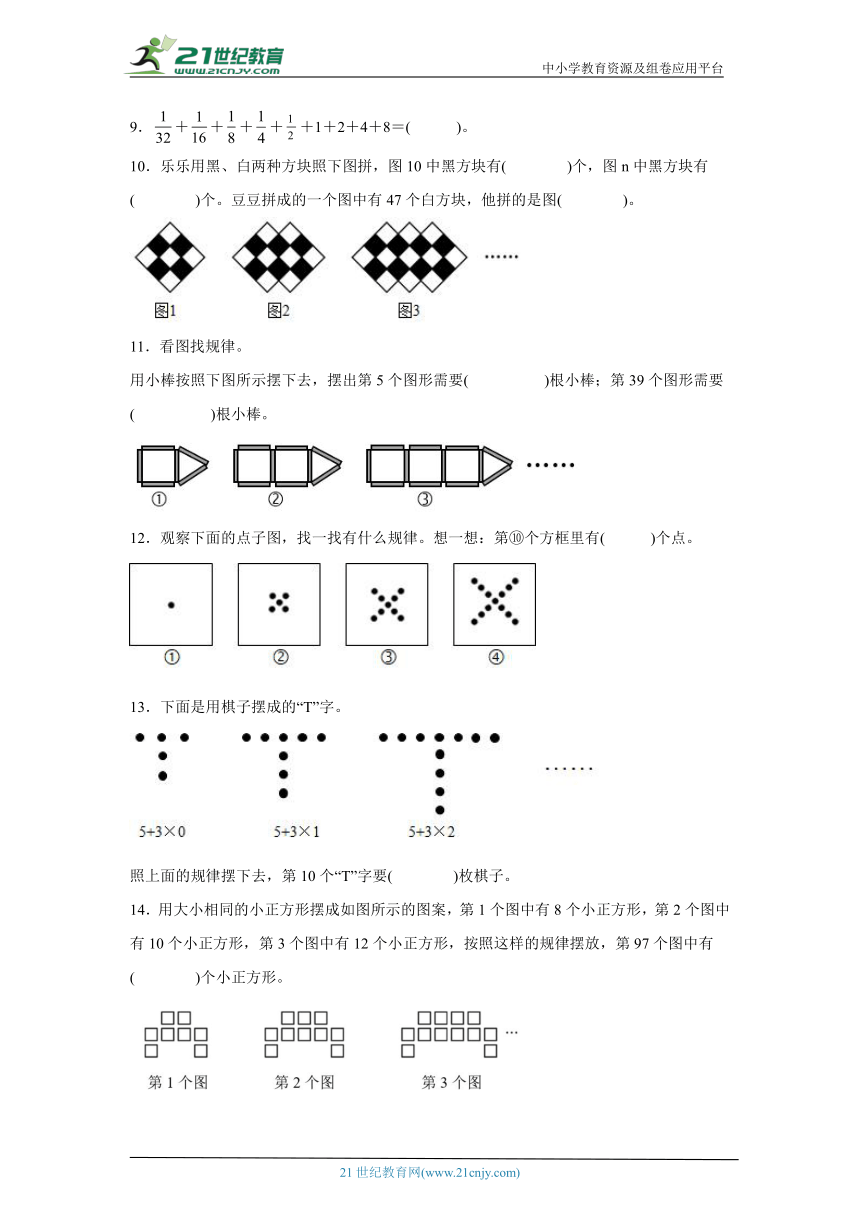
10.乐乐用黑、白两种方块照下图拼,图10中黑方块有( )个,图n中黑方块有( )个。豆豆拼成的一个图中有47个白方块,他拼的是图( )。
11.看图找规律。
用小棒按照下图所示摆下去,摆出第5个图形需要( )根小棒;第39个图形需要( )根小棒。2-1-c-n-j-y
12.观察下面的点子图,找一找有什么规律。想一想:第⑩个方框里有( )个点。
13.下面是用棋子摆成的“T”字。
照上面的规律摆下去,第10个“T”字要( )枚棋子。
14.用大小相同的小正方形摆成如图所示的图案,第1个图中有8个小正方形,第2个图中有10个小正方形,第3个图中有12个小正方形,按照这样的规律摆放,第97个图中有( )个小正方形。
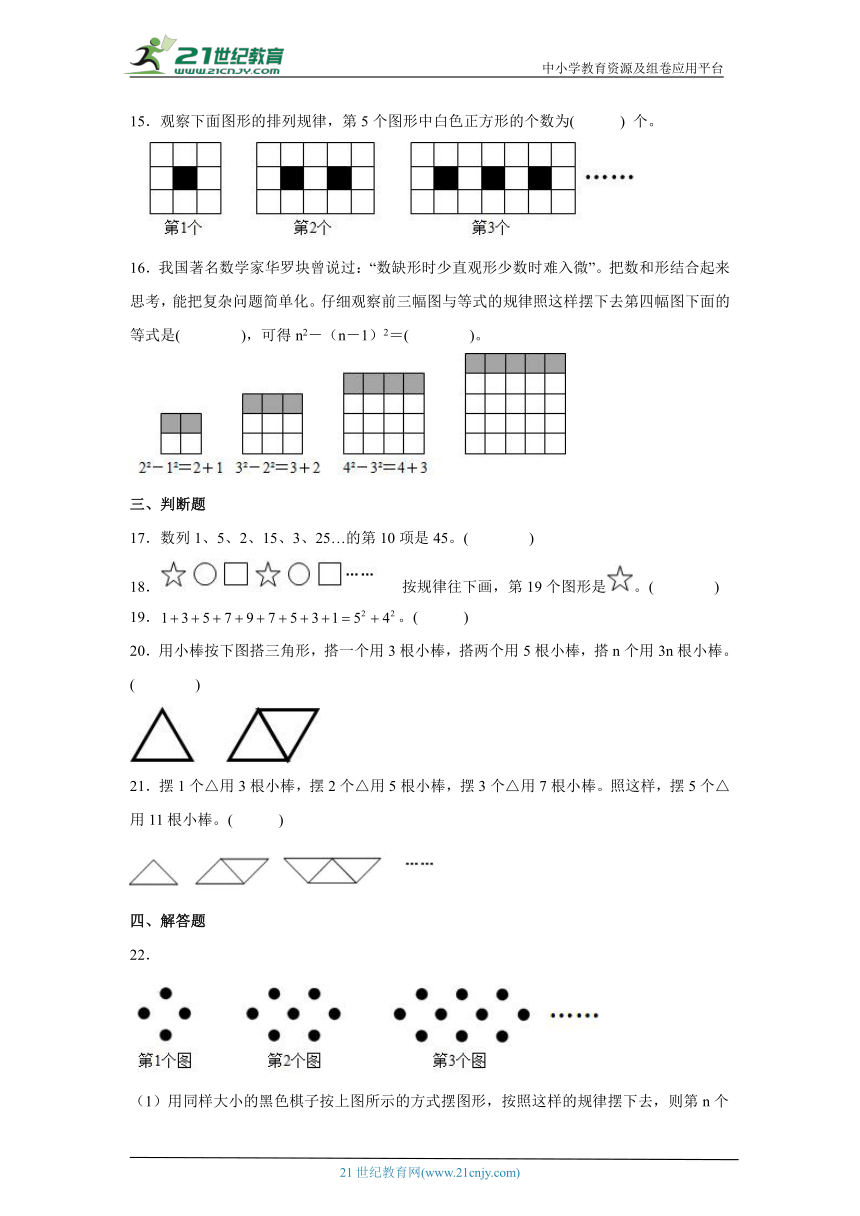
15.观察下面图形的排列规律,第5个图形中白色正方形的个数为( ) 个。
16.我国著名数学家华罗块曾说过:“数缺形时少直观形少数时难入微”。把数和形结合起来思考,能把复杂问题简单化。仔细观察前三幅图与等式的规律照这样摆下去第四幅图下面的等式是( ),可得n2-(n-1)2=( )。
三、判断题
17.数列1、5、2、15、3、25…的第10项是45。( )
18.按规律往下画,第19个图形是。( )
19.。( )
20.用小棒按下图搭三角形,搭一个用3根小棒,搭两个用5根小棒,搭n个用3n根小棒。( )
21.摆1个△用3根小棒,摆2个△用5根小棒,摆3个△用7根小棒。照这样,摆5个△用11根小棒。( )21世纪教育网版权所有
四、解答题
22.
(1)用同样大小的黑色棋子按上图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需要黑色棋子( )枚。(用含n的代数式表示)
(2)用第(1)题中的式子计算第22个图形中有多少枚黑色棋子。
23.下边球体上画出了三个圆,在图中的六个□里分别填入1,2,3,4,5,6,使得每个圆周上四个数相加的和都相等。
(1)这个相等的和等于______;
(2)在图中将所有的□填完整。
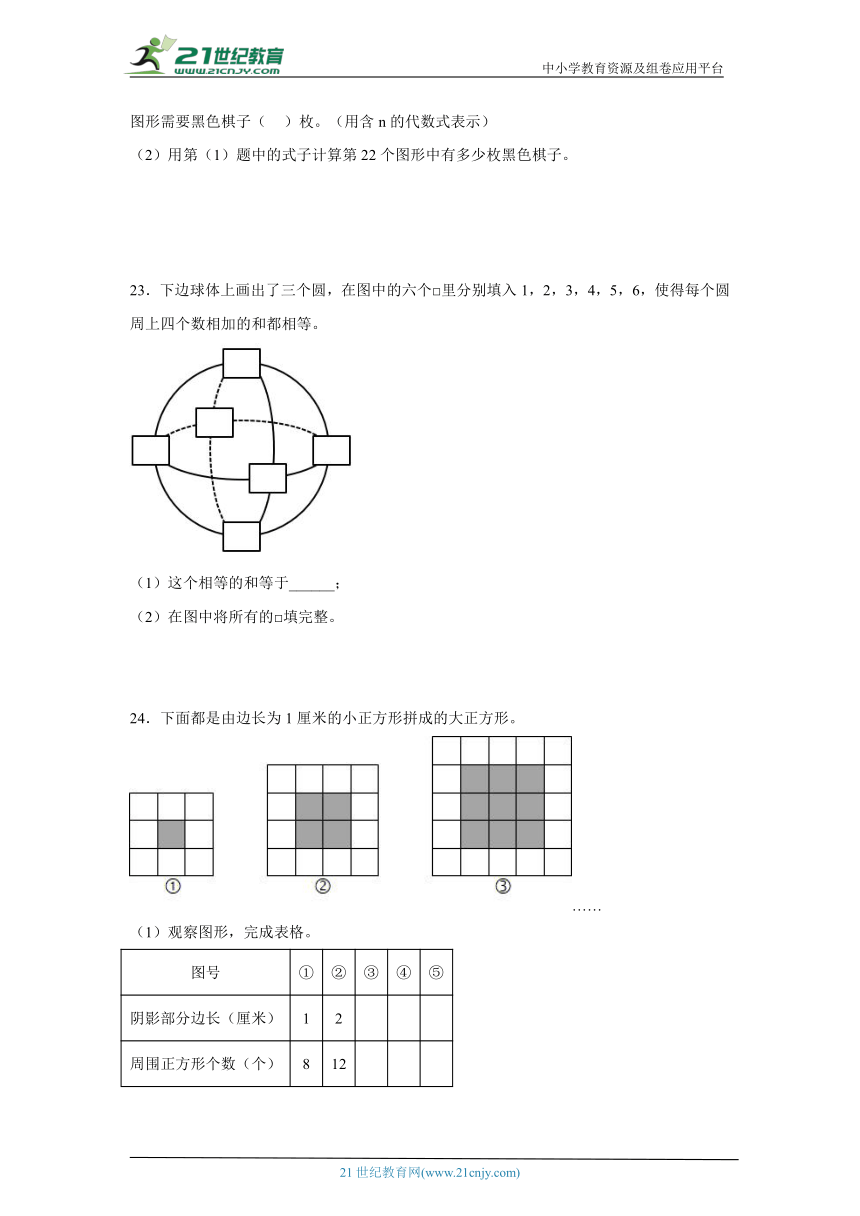
24.下面都是由边长为1厘米的小正方形拼成的大正方形。
……
(1)观察图形,完成表格。
图号 ① ② ③ ④ ⑤
阴影部分边长(厘米) 1 2
周围正方形个数(个) 8 12
(2)以此类推,你知道图⑨中涂色部分的周围共有多少个小正方形吗?
25.找规律,并计算。
观察下列两组等式:
第一组:;;。
第二组:;;;。
回答下列问题:
(1)我发现的规律:两个分数的( )相同,并且等于分母之( ),则这两个分数的和就等于它们的积。21·世纪*教育网
(2)根据这个规律计算:
①;
②若,则正整数m等于( )。
26.某机器有依次排列的5盏灯,每盏灯可发出红色的光(用■表示),不同位置上的灯光表示一个具体的数,下面是四种情况所表示的数。
■□□□□→1;□■□□□→2;■■■□□→7=1+2+4;■□■□■→21=1+4+16
(1)通过观察比较发现:5盏灯中最中间的一盏灯为红色时表示的数是( )。
(2)根据上面的规律,算出下面两种情况所表示的数。(直接填结果)
□□■■■→( )■■□■□→( )
(3)根据下面数的大小,涂出相应红灯的位置。
□□□□□→6 □□□□□→13
27.“贝尔数”是以美国数学家的名字命名的一组整数数列。它的排列形状像个三角形,又称“贝尔三角形”。请认真观察下面数列,并完成问题。21*cnjy*com
(1)第5行第一个数“15”是怎么得到的?
(2)填出第5行两个括号中的数。
参考答案:
1.D
【分析】由图可知,横轴表示时间,纵轴表示速度,折线向上表示加速,折线向下表示减速,折线与横轴平行表示汽车匀速行驶,据此逐项分析。【来源:21cnj*y.co*m】
【详解】A.汽车先静止,再开始发动,加速之后再减速,接着匀速行驶一段距离后加速下坡,最后减速行驶;
B.汽车先静止,再开始发动,加速之后匀速行驶一段距离,再加速下坡,接着减速上坡,最后匀速行驶;
C.汽车一直在行驶,先加速,再匀速行驶一段距离,接着减速,然后加速下坡,再减速上坡,最后匀速行驶;
D.汽车先静止,再开始发动,加速到一定速度匀速行驶一段距离后减速上坡,再加速下坡,接着逐渐减速,最后匀速行驶。
故答案为:D
【点睛】理解折线统计图中每段折线表示的意义是解答题目的关键。
2.D
【分析】由图可知,每个正三角形按上、左下、右下的顺序,三个顶点处是三个连续的自然数,把三个连续自然数看作一个周期,用2008除以3得到三角形的个数,如果商是整数且没有余数,那么商是三角形的个数,第2008个数在三角形的右下顶点处;如果商是整数并且有余数,那么(商+1)是三角形的个数,余数是几,就按照上、左下、右下的顺序数出对应的顶点,据此解答。
【详解】2008÷3=669……1
669+1=670(个)
所以,2008是第670个三角形的上顶点处。
故答案为:D
【点睛】本题主要考查利用数形结合的思想解决问题,根据图形找出数字变化的规律是解答题目的关键。
3.A
【分析】摆1个梯形需要4根小棒,摆2个梯形需要(4+3)根小棒,摆3个梯形需要(4+3×2)根小棒,摆4个梯形需要(4+3×3)根小棒……每增加一个梯形增加3根小棒,摆n个梯形需要[4+3×(n-1)]根小棒,据此解答。
【详解】分析可知,摆n个梯形需要小棒的数量为:4+3×(n-1)
=4+3n-3
=(3n+1)根
所以,摆n个梯形需要(3n+1)根小棒。
故答案为:A
【点睛】分析图形找出梯形个数与小棒根数的变化规律是解答题目的关键。
4.B
【分析】观察可知,小棒数量=六边形数量×5+1,据此分析。
【详解】n×5+1=5n+1=1+5n
故答案为:B
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
5.C
【分析】观察图形,第1个图形白色砖的数量是:4=3+1;
第2个图形白色砖的数量是:7=3×2+1;
第3个图形白色砖的数量是:10=3×3+1;
可以得出规律:第n个蝴蝶图案中白色地砖有块;据此解答。
【详解】由分析可知,第n个蝴蝶图案中白色地砖有块,
当时,白色地砖数量为3×7+1=22(块)。
【点睛】此题考查了数与形的规律问题,关键是结合图形数量之间的运算关系,找出规律即可。
6.D
【分析】观察图形可知:
第一个图形中有5个黑色圆点,即(3+1×2)个;
第二个图形中有14个黑色圆点,即(3+5+2×3)个;
第三个图形中有27个黑色圆点,即(3+5+7+3×4)个;
……
以此类推,第n个图形中黑色圆点的个数为:3+5+7+……+(2n+1)+n(n+1),据此解答即可。www.21-cn-jy.com
【详解】由分析可知,第6个图形中黑色圆点的个数为:
3+5+7+9+11+13+6×7
=48+42
=90(个)
故答案为:D
【点睛】本题主要考查图形的变化规律,关键是根据所给图示,找出规律,并利用规律解答。
7.A
【分析】由题意可知,第几行有几个数,每行第一个数和最后一个数都是1,中间的数等于上面一行对应两个数的和,据此找出第6行的6个数,最后求出所有数的和。
【详解】分析可知,第6行的数为:1、5、10、10、5、1。
1+5+10+10+5+1
=(1+1)+(5+5)+(10+10)
=2+10+20
=32
故答案为:A
【点睛】根据每行数的变化规律准确找出第6行的所有数是解答题目的关键。
8.A
【分析】第几个图中就有几层,且每层圆的个数与层数相同,据此把各层圆的个数进行求和解答。
【详解】图①中圆的个数:1=1
图②中圆的个数:3=1+2
图③中圆的个数:6=1+2+3
图④中圆的个数:10=1+2+3+4
……
图⑩中圆的个数:55=1+2+3+4+……+10
故答案为:A
【点睛】本题考查运用数形结合的方法探究数学规律,注意要把图形和数一一对应。
9.
【分析】根据规律: 的和等于1减去最后一个分数,来计算;再计算1+2+4+8;最后把两次计算的和加起来。
【详解】==
1+2+4+8=15
=
所以原式=
【点睛】在分数和整数混合的加法算式中,可采用“同形结合法”,即整数和整数相加,分数和分数相加。
10. 22 2n+2 15
【分析】图1中黑方块的个数4个,可以写作:2×(1+1)个,图2中黑方块个数有6个,可以写作:2×(2+1)个;图3中黑方块个数有8个,可以写作:2×(3+1)个,……,图n中有黑方块个数为2×(n+1)=2n+2个;由此求出图10中,黑方块的个数;
图1中白方块的个数5个,可写作:5+3×(1-1)个,图2中白方块的个数8个,可写作:5+3×(2-1)个;图3中有白方块个数11个,可写作:5+3×(3-1)个,……,图n中有白方块个数为5+3×(n-1)个,计算出白方块是47个是图几。【来源:21·世纪·教育·网】
【详解】根据分析可知,图10中有黑方块个数:
2×(10+1)
=2×11
=22(个)
图n中有黑方块个数:
2×(n+1)
=(2n+1)个
(47-5)÷3+1
=42÷3+1
=14+1
=15
乐乐用黑、白两种方块照下图拼,图10中黑方块有22个,图n中黑方块有(2n+2)个。豆豆拼成的一个图中有47个白方块,他拼的是图15。2·1·c·n·j·y
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
11. 18 120
【分析】摆出第1个图形需要6根小棒,即3×1+3;
摆出第2个图形需要9根小棒,即3×2+3;
摆出第3个图形需要13根小棒,即3×3+3;
……
摆出第n个图形需要的小棒数为:3n+3。
【详解】由分析可知,摆出第n个图形需要的小棒数为:3n+3。
当n=5时,
3×5+3
=15+3
=18(根)
当n=39时,
3×39+3
=117+3
=120(根)
摆出第5个图形需要18根小棒;第39个图形需要120根小棒。
【点睛】本题主要考查数与形结合的规律,发现每多摆1个图形就多3根小棒是解答本题的关键。
12.37
【分析】第①个方框里有1个点,1=1×4-3;
第②个方框里有5个点,5=2×4-3;
第③个方框里有9个点,9=3×4-3;
第④个方框里有13个点,13=4×4-3;
……
第n个方框里有点的个数:(4n-3)个;
据此规律解答。
【详解】第⑩个方框里有点的个数:
4×10-3
=40-3
=37(个)
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
13.32
【分析】由图可知:第1图有5枚棋子,即(5+3×0)枚;第2图有8枚棋子,即(5+3×1)枚;第3图有11枚棋子,即(5+3×2)枚……第n个图有棋子5+3×(n-1)枚;则第10个图有5+3×(10-1)枚;据此解答即可。21·cn·jy·com
【详解】由分析得:
第10个“T”字有棋子:
5+3×(10-1)
=5+3×9
=5+27
=32(枚)
照上面的规律摆下去,第10个“T”字要32枚棋子。
【点睛】本题主要考查学生通过图形排列的方式,探索规律及归纳总结的能力。
14.200
【分析】第1个图中有8个小正方形,8=2×1+6;
第2个图中有10个小正方形,10=2×2+6;
第3个图中有12个小正方形,12=2×3+6;
……
第n个图中的小正方形有(2n+6)个;
据此规律解答。
【详解】根据分析可知,第n个图中的小正方形有(2n+6)个;
当n=97时
2×97+6
=194+6
=200(个)
用大小相同的小正方形摆成如图所示的图案,第1个图中有8个小正方形,第2个图中有10个小正方形,第3个图中有12个小正方形,按照这样的规律摆放,第97个图中有200个。【出处:21教育名师】
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
15.28
【分析】第1个图有白色正方形8个,8=5×1+3;
第2个图有白色正方形13个,13=5×2+3;
第3个图有白色正方形18个,18=5×3+3;
……
第n个图有白色正方形(5n+3)个;
据此规律求解。
【详解】第5个图形中白色正方形的个数为:
5×5+3
=25+3
=28(个)
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
16. 52-42=5+4 2n-1
【分析】由图可得:图一的算式为22-12=2+1,图二的算式为32-22=3+2,图三的算式为42-32=4+3,由此可得:两个相邻数的平方差等于这两个数的和,且第几幅图,减数就是几,由此列出第四幅图的等式即可,再根据规律算出n2-(n-1)2的结果即可。
【详解】图一:22-12=2+1
图二:32-22=3+2
图三:42-32=4+3
根据规律可得图四:52-42=5+4
n2-(n-1)2
=n+n-1
=2n-1
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
17.√
【分析】观察数列,奇数项是1、2、3…,从1开始依次递增,所以第7项是4,第9项是5,偶数是5、15、25…,15-5=10,25-15=10,后一项比前一项多10,所以第8项=25+10=35,第10项=35+10=45。据此解答。【版权所有:21教育】
【详解】根据分析得,第10项=25+10+10=45。
故答案为:√
【点睛】此题的解题关键是找到数列中数的变化规律。
18.√
【分析】观察这组图形可得3个图形是一个周期,求第n个图形是什么,则用n÷3,得出的余数是1时则与第一个图形相同;得出的余数是2时则与第二个图形相同;没有余数时即与第三个图形相同。21教育名师原创作品
【详解】19÷3=6……1,
所以第19个图形与第一个图形相同,是,即正确。
故答案为:√
【点睛】此题考查是的找规律,正确找出规律并用规律解决问题是解题关键。
19.√
【分析】从1开始的连续奇数相加,和等于奇数个数的平方,据此解答即可。
【详解】
故答案为:√。
【点睛】本题考查数与形,解答本题的关键是掌握题中相加数字的和的规律。
20.×
【分析】根据题图可知,每增加1个三角形小棒就增加2根,当搭n个三角形时,需要的小棒个数为3+2(n-1)=(2n+1)根,据此解答即可。21*cnjy*com
【详解】用小棒搭三角形,搭一个用3根小棒,搭两个用5根小棒,搭n个用(2n+1)根小棒,原题说法错误;
故答案为:×
【点睛】明确每增加1个三角形就增加2根小棒是解答本题的关键,进而总结出规律。
21.√
【分析】根据小棒数量=三角形数量×2+1,计算即可。
【详解】5×2+1
=10+1
=11(根)
故答案为:√
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
22.(1)3n+1
(2)67枚
【分析】(1)观察图形可知,第一幅图需要4枚黑色棋子,第二幅图需要7枚黑色棋子,第三幅图需要10枚黑色棋子,则第n个图形需要黑色棋子(3n+1)枚;
(2)把22代入到式子3n+1中进行计算即可。
【详解】(1)第n个图形需要黑色棋子(3n+1)枚。
(2)当n=22时,代入到式子中得:
3n+1=3×22+1
=66+1
=67
答:第22个图形中有67枚黑色棋子。
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
23.(1)14
(2)见详解
【分析】(1)观察图形可知,1,2,3,4,5,6,在三个圆中各用到2次,先求出它们的和的2倍,再除以3即为所求;21cnjy.com
(2)让每个圆的相对的2个数字的和为7,进行填写即可。
【详解】(1)(1+2+3+4+5+6)×2÷3
=21×2÷3
=14
(2)如图所示:
【点睛】考查了发现规律,求出相等的和是解题的关键。
24.(1)3;4;5
16;20;24
(2)40个
【分析】通过观察图可知:阴影部分边长×4,可求出阴影部分四边的正方形个数,再加上4个角上的4个小正方形,就是周围正方形个数。
【详解】(1)观察图形,完成表格。
图号 ① ② ③ ④ ⑤
阴影部分边长(厘米) 1 2 3 4 5
周围正方形个数(个) 8 12 16 20 24
(2)9×4+4
=36+4
=40(个)
以此类推,你知道图⑨中涂色部分的周围共有40个小正方形。
【点睛】通过观察图得出规律是解答此题的关键。
25.(1)分子,和
(2)①
②19
【分析】(1)观察算式可知,若两个分数的分子相同,且分母之和等于分子,所以这两个分数的和等于它们的积;21教育网
(2)①根据(1)中发现的规律进行计算即可;
②根据规律可知=,然后根据发现的规律求出m的值即可。
【详解】(1)我发现的规律:两个分数的分子相同,并且等于分母之和,则这两个分数的和就等于它们的积。
(2)①
②
=
=
所以6+m=25
m=19
【点睛】本题考查算式的变化规律,发现规律,利用规律是解题的关键。
26.(1)4;(2)28;11;(3)见详解
【分析】(1)由已知的四种情况可知有以下规律:左起第一盏发出红光表示1,后面每一盏灯发出红光时表示的数是前一盏灯的2倍,当几盏灯同时发出红光时表示的数是这几盏灯分别表示的数的和;
(2)根据第(1)题的规律,第1个涂色表示1,第2个涂色表示2,第3个涂色表示4,第4个涂色表示8,第5个涂色表示16,根据此规律按题目要求把已经涂色的红灯表示的数相加即可得解;
(3)根据6=2+4,把第2个和第3个涂色,根据13=1+4+8,把第1个、第3个和第4个方框涂色,据此解答即可。
【详解】(1)1×2=2
2×2=4
4×2=8
8×2=16
所以5盏灯中最中间的一盏灯为红色时表示的数是4。
(2)4+8+16=28
1+2+8=11
所以□□■■■→28,■■□■□→11。
(3)6=2+4
13=1+4+8
所以发红光的灯的位置如下:
□■■□□→6
■□■■□→13
【点睛】解答此题的关键在于通过已知的例子找出每盏灯发红光时表示的数,再根据规律解答。
27.(1)第5行第一个数“15”是通过第四行的最后一个数得来的;
(2)27;52
【分析】(1)仔细观察得知,每排的最后一个数都等于下一排的第一个数;
(2)其他任何一个数等于它左边相邻数加左边相邻数上面的一个数。
【详解】(1)通过分析可知,第5行第一个数“15”是通过第四行的最后一个数得来的;
(2)20+7=27;37+15=52
【点睛】本题是一道探究规律的题目,根据已知数字确定数形中的规律是解答的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第8单元数学广角-数与形练习卷-小学数学六年级上册人教版
一、选择题
1.下图能够大概描述汽车由静止开始发动,加速到一定速度匀速行驶一段距离后减速上坡,再加速下坡,然后逐渐减速到匀速行驶的过程是( )。www-2-1-cnjy-com
A. B.
C. D.
2.如图,观察下列正三角形的三个顶点所标的数字规律,那么2008这个数在第( )个三角形的( )顶点处。( )
A.669;上 B.669;左下 C.670;右下 D.670;上
3.像这样摆下去,n个梯形需要的小棒根数是( )根。
A. B. C.
4.按规律摆六边形,如果摆n个六边形,需要( )根小棒。
A.6n B. C.
5.如图所示,用黑白两种颜色的正五边形地砖按下图所示的规律,拼成若干个蝴蝶图案,则第7个蝴蝶图案中白色地砖有( )。
A.35块 B.27块 C.22块 D.7块
6.下列图形都是由同样大小的黑色圆点按照一定规律所组成的,其中第1个图形中一共有5个黑色圆点,第2个图形中一共有14个黑色圆点,第3个图形中一共有27个黑色圆点……按此规律排列下去,第6个图形中有( )个黑色圆点。
A.65 B.91 C.78 D.90
7.如图是“杨辉三角”,根据各数之间的关系,第6行中所有数的和是( )。
A.32 B.22 C.20
8.观察下边图形,按此规律,第⑩个图中○的个数有( )个。
A.55 B.40 C.36 D.10
二、填空题
9.+++++1+2+4+8=( )。
10.乐乐用黑、白两种方块照下图拼,图10中黑方块有( )个,图n中黑方块有( )个。豆豆拼成的一个图中有47个白方块,他拼的是图( )。
11.看图找规律。
用小棒按照下图所示摆下去,摆出第5个图形需要( )根小棒;第39个图形需要( )根小棒。2-1-c-n-j-y
12.观察下面的点子图,找一找有什么规律。想一想:第⑩个方框里有( )个点。
13.下面是用棋子摆成的“T”字。
照上面的规律摆下去,第10个“T”字要( )枚棋子。
14.用大小相同的小正方形摆成如图所示的图案,第1个图中有8个小正方形,第2个图中有10个小正方形,第3个图中有12个小正方形,按照这样的规律摆放,第97个图中有( )个小正方形。
15.观察下面图形的排列规律,第5个图形中白色正方形的个数为( ) 个。
16.我国著名数学家华罗块曾说过:“数缺形时少直观形少数时难入微”。把数和形结合起来思考,能把复杂问题简单化。仔细观察前三幅图与等式的规律照这样摆下去第四幅图下面的等式是( ),可得n2-(n-1)2=( )。
三、判断题
17.数列1、5、2、15、3、25…的第10项是45。( )
18.按规律往下画,第19个图形是。( )
19.。( )
20.用小棒按下图搭三角形,搭一个用3根小棒,搭两个用5根小棒,搭n个用3n根小棒。( )
21.摆1个△用3根小棒,摆2个△用5根小棒,摆3个△用7根小棒。照这样,摆5个△用11根小棒。( )21世纪教育网版权所有
四、解答题
22.
(1)用同样大小的黑色棋子按上图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需要黑色棋子( )枚。(用含n的代数式表示)
(2)用第(1)题中的式子计算第22个图形中有多少枚黑色棋子。
23.下边球体上画出了三个圆,在图中的六个□里分别填入1,2,3,4,5,6,使得每个圆周上四个数相加的和都相等。
(1)这个相等的和等于______;
(2)在图中将所有的□填完整。
24.下面都是由边长为1厘米的小正方形拼成的大正方形。
……
(1)观察图形,完成表格。
图号 ① ② ③ ④ ⑤
阴影部分边长(厘米) 1 2
周围正方形个数(个) 8 12
(2)以此类推,你知道图⑨中涂色部分的周围共有多少个小正方形吗?
25.找规律,并计算。
观察下列两组等式:
第一组:;;。
第二组:;;;。
回答下列问题:
(1)我发现的规律:两个分数的( )相同,并且等于分母之( ),则这两个分数的和就等于它们的积。21·世纪*教育网
(2)根据这个规律计算:
①;
②若,则正整数m等于( )。
26.某机器有依次排列的5盏灯,每盏灯可发出红色的光(用■表示),不同位置上的灯光表示一个具体的数,下面是四种情况所表示的数。
■□□□□→1;□■□□□→2;■■■□□→7=1+2+4;■□■□■→21=1+4+16
(1)通过观察比较发现:5盏灯中最中间的一盏灯为红色时表示的数是( )。
(2)根据上面的规律,算出下面两种情况所表示的数。(直接填结果)
□□■■■→( )■■□■□→( )
(3)根据下面数的大小,涂出相应红灯的位置。
□□□□□→6 □□□□□→13
27.“贝尔数”是以美国数学家的名字命名的一组整数数列。它的排列形状像个三角形,又称“贝尔三角形”。请认真观察下面数列,并完成问题。21*cnjy*com
(1)第5行第一个数“15”是怎么得到的?
(2)填出第5行两个括号中的数。
参考答案:
1.D
【分析】由图可知,横轴表示时间,纵轴表示速度,折线向上表示加速,折线向下表示减速,折线与横轴平行表示汽车匀速行驶,据此逐项分析。【来源:21cnj*y.co*m】
【详解】A.汽车先静止,再开始发动,加速之后再减速,接着匀速行驶一段距离后加速下坡,最后减速行驶;
B.汽车先静止,再开始发动,加速之后匀速行驶一段距离,再加速下坡,接着减速上坡,最后匀速行驶;
C.汽车一直在行驶,先加速,再匀速行驶一段距离,接着减速,然后加速下坡,再减速上坡,最后匀速行驶;
D.汽车先静止,再开始发动,加速到一定速度匀速行驶一段距离后减速上坡,再加速下坡,接着逐渐减速,最后匀速行驶。
故答案为:D
【点睛】理解折线统计图中每段折线表示的意义是解答题目的关键。
2.D
【分析】由图可知,每个正三角形按上、左下、右下的顺序,三个顶点处是三个连续的自然数,把三个连续自然数看作一个周期,用2008除以3得到三角形的个数,如果商是整数且没有余数,那么商是三角形的个数,第2008个数在三角形的右下顶点处;如果商是整数并且有余数,那么(商+1)是三角形的个数,余数是几,就按照上、左下、右下的顺序数出对应的顶点,据此解答。
【详解】2008÷3=669……1
669+1=670(个)
所以,2008是第670个三角形的上顶点处。
故答案为:D
【点睛】本题主要考查利用数形结合的思想解决问题,根据图形找出数字变化的规律是解答题目的关键。
3.A
【分析】摆1个梯形需要4根小棒,摆2个梯形需要(4+3)根小棒,摆3个梯形需要(4+3×2)根小棒,摆4个梯形需要(4+3×3)根小棒……每增加一个梯形增加3根小棒,摆n个梯形需要[4+3×(n-1)]根小棒,据此解答。
【详解】分析可知,摆n个梯形需要小棒的数量为:4+3×(n-1)
=4+3n-3
=(3n+1)根
所以,摆n个梯形需要(3n+1)根小棒。
故答案为:A
【点睛】分析图形找出梯形个数与小棒根数的变化规律是解答题目的关键。
4.B
【分析】观察可知,小棒数量=六边形数量×5+1,据此分析。
【详解】n×5+1=5n+1=1+5n
故答案为:B
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
5.C
【分析】观察图形,第1个图形白色砖的数量是:4=3+1;
第2个图形白色砖的数量是:7=3×2+1;
第3个图形白色砖的数量是:10=3×3+1;
可以得出规律:第n个蝴蝶图案中白色地砖有块;据此解答。
【详解】由分析可知,第n个蝴蝶图案中白色地砖有块,
当时,白色地砖数量为3×7+1=22(块)。
【点睛】此题考查了数与形的规律问题,关键是结合图形数量之间的运算关系,找出规律即可。
6.D
【分析】观察图形可知:
第一个图形中有5个黑色圆点,即(3+1×2)个;
第二个图形中有14个黑色圆点,即(3+5+2×3)个;
第三个图形中有27个黑色圆点,即(3+5+7+3×4)个;
……
以此类推,第n个图形中黑色圆点的个数为:3+5+7+……+(2n+1)+n(n+1),据此解答即可。www.21-cn-jy.com
【详解】由分析可知,第6个图形中黑色圆点的个数为:
3+5+7+9+11+13+6×7
=48+42
=90(个)
故答案为:D
【点睛】本题主要考查图形的变化规律,关键是根据所给图示,找出规律,并利用规律解答。
7.A
【分析】由题意可知,第几行有几个数,每行第一个数和最后一个数都是1,中间的数等于上面一行对应两个数的和,据此找出第6行的6个数,最后求出所有数的和。
【详解】分析可知,第6行的数为:1、5、10、10、5、1。
1+5+10+10+5+1
=(1+1)+(5+5)+(10+10)
=2+10+20
=32
故答案为:A
【点睛】根据每行数的变化规律准确找出第6行的所有数是解答题目的关键。
8.A
【分析】第几个图中就有几层,且每层圆的个数与层数相同,据此把各层圆的个数进行求和解答。
【详解】图①中圆的个数:1=1
图②中圆的个数:3=1+2
图③中圆的个数:6=1+2+3
图④中圆的个数:10=1+2+3+4
……
图⑩中圆的个数:55=1+2+3+4+……+10
故答案为:A
【点睛】本题考查运用数形结合的方法探究数学规律,注意要把图形和数一一对应。
9.
【分析】根据规律: 的和等于1减去最后一个分数,来计算;再计算1+2+4+8;最后把两次计算的和加起来。
【详解】==
1+2+4+8=15
=
所以原式=
【点睛】在分数和整数混合的加法算式中,可采用“同形结合法”,即整数和整数相加,分数和分数相加。
10. 22 2n+2 15
【分析】图1中黑方块的个数4个,可以写作:2×(1+1)个,图2中黑方块个数有6个,可以写作:2×(2+1)个;图3中黑方块个数有8个,可以写作:2×(3+1)个,……,图n中有黑方块个数为2×(n+1)=2n+2个;由此求出图10中,黑方块的个数;
图1中白方块的个数5个,可写作:5+3×(1-1)个,图2中白方块的个数8个,可写作:5+3×(2-1)个;图3中有白方块个数11个,可写作:5+3×(3-1)个,……,图n中有白方块个数为5+3×(n-1)个,计算出白方块是47个是图几。【来源:21·世纪·教育·网】
【详解】根据分析可知,图10中有黑方块个数:
2×(10+1)
=2×11
=22(个)
图n中有黑方块个数:
2×(n+1)
=(2n+1)个
(47-5)÷3+1
=42÷3+1
=14+1
=15
乐乐用黑、白两种方块照下图拼,图10中黑方块有22个,图n中黑方块有(2n+2)个。豆豆拼成的一个图中有47个白方块,他拼的是图15。2·1·c·n·j·y
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
11. 18 120
【分析】摆出第1个图形需要6根小棒,即3×1+3;
摆出第2个图形需要9根小棒,即3×2+3;
摆出第3个图形需要13根小棒,即3×3+3;
……
摆出第n个图形需要的小棒数为:3n+3。
【详解】由分析可知,摆出第n个图形需要的小棒数为:3n+3。
当n=5时,
3×5+3
=15+3
=18(根)
当n=39时,
3×39+3
=117+3
=120(根)
摆出第5个图形需要18根小棒;第39个图形需要120根小棒。
【点睛】本题主要考查数与形结合的规律,发现每多摆1个图形就多3根小棒是解答本题的关键。
12.37
【分析】第①个方框里有1个点,1=1×4-3;
第②个方框里有5个点,5=2×4-3;
第③个方框里有9个点,9=3×4-3;
第④个方框里有13个点,13=4×4-3;
……
第n个方框里有点的个数:(4n-3)个;
据此规律解答。
【详解】第⑩个方框里有点的个数:
4×10-3
=40-3
=37(个)
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
13.32
【分析】由图可知:第1图有5枚棋子,即(5+3×0)枚;第2图有8枚棋子,即(5+3×1)枚;第3图有11枚棋子,即(5+3×2)枚……第n个图有棋子5+3×(n-1)枚;则第10个图有5+3×(10-1)枚;据此解答即可。21·cn·jy·com
【详解】由分析得:
第10个“T”字有棋子:
5+3×(10-1)
=5+3×9
=5+27
=32(枚)
照上面的规律摆下去,第10个“T”字要32枚棋子。
【点睛】本题主要考查学生通过图形排列的方式,探索规律及归纳总结的能力。
14.200
【分析】第1个图中有8个小正方形,8=2×1+6;
第2个图中有10个小正方形,10=2×2+6;
第3个图中有12个小正方形,12=2×3+6;
……
第n个图中的小正方形有(2n+6)个;
据此规律解答。
【详解】根据分析可知,第n个图中的小正方形有(2n+6)个;
当n=97时
2×97+6
=194+6
=200(个)
用大小相同的小正方形摆成如图所示的图案,第1个图中有8个小正方形,第2个图中有10个小正方形,第3个图中有12个小正方形,按照这样的规律摆放,第97个图中有200个。【出处:21教育名师】
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
15.28
【分析】第1个图有白色正方形8个,8=5×1+3;
第2个图有白色正方形13个,13=5×2+3;
第3个图有白色正方形18个,18=5×3+3;
……
第n个图有白色正方形(5n+3)个;
据此规律求解。
【详解】第5个图形中白色正方形的个数为:
5×5+3
=25+3
=28(个)
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
16. 52-42=5+4 2n-1
【分析】由图可得:图一的算式为22-12=2+1,图二的算式为32-22=3+2,图三的算式为42-32=4+3,由此可得:两个相邻数的平方差等于这两个数的和,且第几幅图,减数就是几,由此列出第四幅图的等式即可,再根据规律算出n2-(n-1)2的结果即可。
【详解】图一:22-12=2+1
图二:32-22=3+2
图三:42-32=4+3
根据规律可得图四:52-42=5+4
n2-(n-1)2
=n+n-1
=2n-1
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
17.√
【分析】观察数列,奇数项是1、2、3…,从1开始依次递增,所以第7项是4,第9项是5,偶数是5、15、25…,15-5=10,25-15=10,后一项比前一项多10,所以第8项=25+10=35,第10项=35+10=45。据此解答。【版权所有:21教育】
【详解】根据分析得,第10项=25+10+10=45。
故答案为:√
【点睛】此题的解题关键是找到数列中数的变化规律。
18.√
【分析】观察这组图形可得3个图形是一个周期,求第n个图形是什么,则用n÷3,得出的余数是1时则与第一个图形相同;得出的余数是2时则与第二个图形相同;没有余数时即与第三个图形相同。21教育名师原创作品
【详解】19÷3=6……1,
所以第19个图形与第一个图形相同,是,即正确。
故答案为:√
【点睛】此题考查是的找规律,正确找出规律并用规律解决问题是解题关键。
19.√
【分析】从1开始的连续奇数相加,和等于奇数个数的平方,据此解答即可。
【详解】
故答案为:√。
【点睛】本题考查数与形,解答本题的关键是掌握题中相加数字的和的规律。
20.×
【分析】根据题图可知,每增加1个三角形小棒就增加2根,当搭n个三角形时,需要的小棒个数为3+2(n-1)=(2n+1)根,据此解答即可。21*cnjy*com
【详解】用小棒搭三角形,搭一个用3根小棒,搭两个用5根小棒,搭n个用(2n+1)根小棒,原题说法错误;
故答案为:×
【点睛】明确每增加1个三角形就增加2根小棒是解答本题的关键,进而总结出规律。
21.√
【分析】根据小棒数量=三角形数量×2+1,计算即可。
【详解】5×2+1
=10+1
=11(根)
故答案为:√
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
22.(1)3n+1
(2)67枚
【分析】(1)观察图形可知,第一幅图需要4枚黑色棋子,第二幅图需要7枚黑色棋子,第三幅图需要10枚黑色棋子,则第n个图形需要黑色棋子(3n+1)枚;
(2)把22代入到式子3n+1中进行计算即可。
【详解】(1)第n个图形需要黑色棋子(3n+1)枚。
(2)当n=22时,代入到式子中得:
3n+1=3×22+1
=66+1
=67
答:第22个图形中有67枚黑色棋子。
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
23.(1)14
(2)见详解
【分析】(1)观察图形可知,1,2,3,4,5,6,在三个圆中各用到2次,先求出它们的和的2倍,再除以3即为所求;21cnjy.com
(2)让每个圆的相对的2个数字的和为7,进行填写即可。
【详解】(1)(1+2+3+4+5+6)×2÷3
=21×2÷3
=14
(2)如图所示:
【点睛】考查了发现规律,求出相等的和是解题的关键。
24.(1)3;4;5
16;20;24
(2)40个
【分析】通过观察图可知:阴影部分边长×4,可求出阴影部分四边的正方形个数,再加上4个角上的4个小正方形,就是周围正方形个数。
【详解】(1)观察图形,完成表格。
图号 ① ② ③ ④ ⑤
阴影部分边长(厘米) 1 2 3 4 5
周围正方形个数(个) 8 12 16 20 24
(2)9×4+4
=36+4
=40(个)
以此类推,你知道图⑨中涂色部分的周围共有40个小正方形。
【点睛】通过观察图得出规律是解答此题的关键。
25.(1)分子,和
(2)①
②19
【分析】(1)观察算式可知,若两个分数的分子相同,且分母之和等于分子,所以这两个分数的和等于它们的积;21教育网
(2)①根据(1)中发现的规律进行计算即可;
②根据规律可知=,然后根据发现的规律求出m的值即可。
【详解】(1)我发现的规律:两个分数的分子相同,并且等于分母之和,则这两个分数的和就等于它们的积。
(2)①
②
=
=
所以6+m=25
m=19
【点睛】本题考查算式的变化规律,发现规律,利用规律是解题的关键。
26.(1)4;(2)28;11;(3)见详解
【分析】(1)由已知的四种情况可知有以下规律:左起第一盏发出红光表示1,后面每一盏灯发出红光时表示的数是前一盏灯的2倍,当几盏灯同时发出红光时表示的数是这几盏灯分别表示的数的和;
(2)根据第(1)题的规律,第1个涂色表示1,第2个涂色表示2,第3个涂色表示4,第4个涂色表示8,第5个涂色表示16,根据此规律按题目要求把已经涂色的红灯表示的数相加即可得解;
(3)根据6=2+4,把第2个和第3个涂色,根据13=1+4+8,把第1个、第3个和第4个方框涂色,据此解答即可。
【详解】(1)1×2=2
2×2=4
4×2=8
8×2=16
所以5盏灯中最中间的一盏灯为红色时表示的数是4。
(2)4+8+16=28
1+2+8=11
所以□□■■■→28,■■□■□→11。
(3)6=2+4
13=1+4+8
所以发红光的灯的位置如下:
□■■□□→6
■□■■□→13
【点睛】解答此题的关键在于通过已知的例子找出每盏灯发红光时表示的数,再根据规律解答。
27.(1)第5行第一个数“15”是通过第四行的最后一个数得来的;
(2)27;52
【分析】(1)仔细观察得知,每排的最后一个数都等于下一排的第一个数;
(2)其他任何一个数等于它左边相邻数加左边相邻数上面的一个数。
【详解】(1)通过分析可知,第5行第一个数“15”是通过第四行的最后一个数得来的;
(2)20+7=27;37+15=52
【点睛】本题是一道探究规律的题目,根据已知数字确定数形中的规律是解答的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
