数学人教A版(2019)必修第一册4.1.1 n次方根与分数指数幂(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.1.1 n次方根与分数指数幂(共25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 851.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 21:37:19 | ||
图片预览








文档简介
(共25张PPT)
良渚遗址位于浙江省杭州市余杭区良渚和瓶窑镇,1936年首次发现. 这里的巨型城址,面积近360万平方米,包括古城、水坝和多处高等级建筑. 考古学家利用遗址中遗存的碳14的残留量测定,古城存在的时期为公元前3300年~2500年,你知道考古学家测定遗址年代用的是什么数学知识吗?
指数函数在解决实际问题中有着广泛的应用.
指数函数
第4章 指数函数与对数函数
4.1 指数
4.1.1 n次方根与分数指数幂
1.理解n次方根、根式的概念.
2.能正确运用根式的性质化简或求值,能进行根式与分数指数幂之间的相互转化.
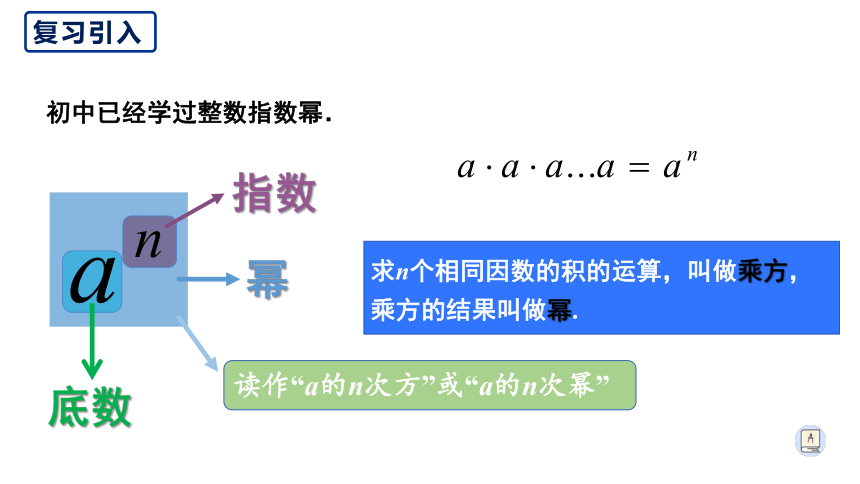
初中已经学过整数指数幂.
幂
指数
底数
读作“a的n次方”或“a的n次幂”
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.
复习引入
2.整数指数幂的运算性质:
1.整数指数幂:
复习引入
积的乘方
同底数幂乘法
幂的乘方
整数指数幂 零指数幂 负指数幂
复习引入
学习幂函数时,我们把正方形场地的边长 c关于面积S的函数
问题:初中阶段我们学过平方根、立方根的概念,你能回想出这些概念吗?能举例说明吗?
因为(±2)2 =4,所以±2叫做4的平方根;
因为(±3)2 =9,所以±3叫做9的平方根;
因为23=8,所以2叫做8的立方根;
因为(-2)3=-8,所以-2叫做-8的立方根;
如果x2=a,那么x叫做a的平方根;
如果x3=a,那么x叫做a的立方根;
xn=a
探究新知
当n是奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,0的n次方根为0,这时,a的n次方根用符号 表示.
例如:
n次方根定义:
一般地,如果xn=a,则x叫做a的n次方根,其中n>1,且n∈N*.
奇次方根
探究新知
(a∈R)
当n是偶数时:正数的n次方根是有两个,这两个数互为相反数
正数a的正的n次方根用符号 表示,负的n次方根用符号 表示.正的n次方根和负的n次方根合并写成 ;
n次方根定义:
一般地,如果xn=a,则x叫做a的n次方根,其中n>1,且n∈N*.
偶次方根
探究新知
(a>0)
负数有没有偶次方根,因为任何实数的偶次方都是非负数.
负数有没有偶次方根?为什么?
?
偶次方根
探究新知
偶次方根
2.负数没有偶次方根;
1.正数的偶次方根有两个且互为相反数;
3.0的偶次方根为0.
0的任何次方根都是0,记作 .
根式:
式子 叫做根式,这里n叫做根指数,a叫做被开方数.
根式
探究新知
(n为奇数,且a R)
(当n是偶数,且a>0)
n次根式性质
一定成立吗?
探究
探究新知
n次根式的性质一:
①当n为奇数时,
②当n为偶数时,
n次根式的性质二:
探究新知
(n为奇数)
(当n是偶数,且a>0)
0的任何次方根都是0,记作 .
根式: 式子 叫做根式,这里n叫做根指数,a叫做被开方数.
n次方根定义: 一般地,如果xn=a,则x叫做a的n次方根,其中n>1,且n∈N*
小结1
性质一:
②当n为偶数时,
性质二:
①当n为奇数时,
例1 求下列各式的值:
(1) ;(2) ;(3) ;(4) .
解:
探究根据n次方根的定义和运算,我们知道
___________________(a>0)
___________________(a>0)
思考 当根式的被开方数的指数不能被根指数整除时,根式是否也能表示为分数指数幂的形式呢?
任何一个根式都可以表示为分数指数幂的形式,例如:
探究新知
当根式的被开方数的指数能被根指数整除时,根式可以表示为分数指数幂的形式。
正数的正分数指数幂:
正数的负分数指数幂:
规定:0的正分数指数幂等于0,0的负分数指数幂没意义.
分数指数幂
探究新知
数学中引进一个新的概念与法则,总希望它与已有的概念或法则相容。
负指数幂
同底数幂相乘,底数不变,指数相加
幂的乘方,底数不变,指数相乘
积的乘方,等于积的每一个因式分别乘方,再把所得的幂相乘
同底数幂相除,底数不变,指数相减
指数运算性质
探究新知
正数的正分数指数幂:
正数的负分数指数幂:
规定:0的正分数指数幂等于0,0的负分数指数幂没意义.
指数运算性质:
小结2
例2 求值:(1);(2).
解:
例3 用分数指数幂的形式表示并计算下列各式( 其中a>0).
; .
例4 计算下式各式(式中字母均是正数).
解:
方法:1.用分数指数幂表示根式,往往会简化运算。
2.运算时尽量化为同底数幂。
(n为奇数)
(当n是偶数,且a>0)
0的任何次方根都是0,记作 .
根式: 式子 叫做根式,这里n叫做根指数,a叫做被开方数.
n次方根定义: 一般地,如果xn=a,则x叫做a的n次方根,其中n>1,且n∈N*
小结
性质一:
②当n为偶数时,
性质二:
①当n为奇数时,
正数的正分数指数幂:
正数的负分数指数幂:
规定:0的正分数指数幂等于0,0的负分数指数幂没意义.
指数运算性质:
小结
良渚遗址位于浙江省杭州市余杭区良渚和瓶窑镇,1936年首次发现. 这里的巨型城址,面积近360万平方米,包括古城、水坝和多处高等级建筑. 考古学家利用遗址中遗存的碳14的残留量测定,古城存在的时期为公元前3300年~2500年,你知道考古学家测定遗址年代用的是什么数学知识吗?
指数函数在解决实际问题中有着广泛的应用.
指数函数
第4章 指数函数与对数函数
4.1 指数
4.1.1 n次方根与分数指数幂
1.理解n次方根、根式的概念.
2.能正确运用根式的性质化简或求值,能进行根式与分数指数幂之间的相互转化.
初中已经学过整数指数幂.
幂
指数
底数
读作“a的n次方”或“a的n次幂”
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.
复习引入
2.整数指数幂的运算性质:
1.整数指数幂:
复习引入
积的乘方
同底数幂乘法
幂的乘方
整数指数幂 零指数幂 负指数幂
复习引入
学习幂函数时,我们把正方形场地的边长 c关于面积S的函数
问题:初中阶段我们学过平方根、立方根的概念,你能回想出这些概念吗?能举例说明吗?
因为(±2)2 =4,所以±2叫做4的平方根;
因为(±3)2 =9,所以±3叫做9的平方根;
因为23=8,所以2叫做8的立方根;
因为(-2)3=-8,所以-2叫做-8的立方根;
如果x2=a,那么x叫做a的平方根;
如果x3=a,那么x叫做a的立方根;
xn=a
探究新知
当n是奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,0的n次方根为0,这时,a的n次方根用符号 表示.
例如:
n次方根定义:
一般地,如果xn=a,则x叫做a的n次方根,其中n>1,且n∈N*.
奇次方根
探究新知
(a∈R)
当n是偶数时:正数的n次方根是有两个,这两个数互为相反数
正数a的正的n次方根用符号 表示,负的n次方根用符号 表示.正的n次方根和负的n次方根合并写成 ;
n次方根定义:
一般地,如果xn=a,则x叫做a的n次方根,其中n>1,且n∈N*.
偶次方根
探究新知
(a>0)
负数有没有偶次方根,因为任何实数的偶次方都是非负数.
负数有没有偶次方根?为什么?
?
偶次方根
探究新知
偶次方根
2.负数没有偶次方根;
1.正数的偶次方根有两个且互为相反数;
3.0的偶次方根为0.
0的任何次方根都是0,记作 .
根式:
式子 叫做根式,这里n叫做根指数,a叫做被开方数.
根式
探究新知
(n为奇数,且a R)
(当n是偶数,且a>0)
n次根式性质
一定成立吗?
探究
探究新知
n次根式的性质一:
①当n为奇数时,
②当n为偶数时,
n次根式的性质二:
探究新知
(n为奇数)
(当n是偶数,且a>0)
0的任何次方根都是0,记作 .
根式: 式子 叫做根式,这里n叫做根指数,a叫做被开方数.
n次方根定义: 一般地,如果xn=a,则x叫做a的n次方根,其中n>1,且n∈N*
小结1
性质一:
②当n为偶数时,
性质二:
①当n为奇数时,
例1 求下列各式的值:
(1) ;(2) ;(3) ;(4) .
解:
探究根据n次方根的定义和运算,我们知道
___________________(a>0)
___________________(a>0)
思考 当根式的被开方数的指数不能被根指数整除时,根式是否也能表示为分数指数幂的形式呢?
任何一个根式都可以表示为分数指数幂的形式,例如:
探究新知
当根式的被开方数的指数能被根指数整除时,根式可以表示为分数指数幂的形式。
正数的正分数指数幂:
正数的负分数指数幂:
规定:0的正分数指数幂等于0,0的负分数指数幂没意义.
分数指数幂
探究新知
数学中引进一个新的概念与法则,总希望它与已有的概念或法则相容。
负指数幂
同底数幂相乘,底数不变,指数相加
幂的乘方,底数不变,指数相乘
积的乘方,等于积的每一个因式分别乘方,再把所得的幂相乘
同底数幂相除,底数不变,指数相减
指数运算性质
探究新知
正数的正分数指数幂:
正数的负分数指数幂:
规定:0的正分数指数幂等于0,0的负分数指数幂没意义.
指数运算性质:
小结2
例2 求值:(1);(2).
解:
例3 用分数指数幂的形式表示并计算下列各式( 其中a>0).
; .
例4 计算下式各式(式中字母均是正数).
解:
方法:1.用分数指数幂表示根式,往往会简化运算。
2.运算时尽量化为同底数幂。
(n为奇数)
(当n是偶数,且a>0)
0的任何次方根都是0,记作 .
根式: 式子 叫做根式,这里n叫做根指数,a叫做被开方数.
n次方根定义: 一般地,如果xn=a,则x叫做a的n次方根,其中n>1,且n∈N*
小结
性质一:
②当n为偶数时,
性质二:
①当n为奇数时,
正数的正分数指数幂:
正数的负分数指数幂:
规定:0的正分数指数幂等于0,0的负分数指数幂没意义.
指数运算性质:
小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
