数学人教A版（2019）必修第一册1.4 充分条件与必要条件（共33张ppt）

(共33张PPT)
第一章 集合与常用逻辑用语
1.4 充分条件与必要条件
学习目标
1.理解充分条件、必要条件、充要条件的概念.（数学抽象）
2.了解充分条件与判定定理，必要条件与性质定理，充要条件与性质定理的关系.（逻辑推理）
3.能通过充分性、必要性解决简单的问题.（逻辑推理）
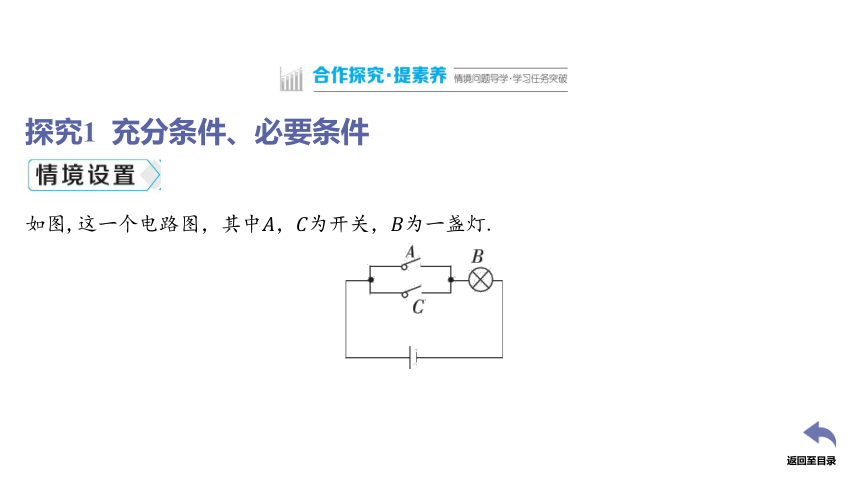
探究1 充分条件、必要条件
如图,这一个电路图，其中，为开关，为一盏灯.
问题1：.开关闭合时，灯一定亮吗？
[答案] 一定.
问题2：.灯亮时开关一定闭合吗？
[答案] 不一定.
问题3：.开关闭合是灯亮的什么条件？
[答案] 充分条件.
目录
CONTENT
（一）复习回顾，创设情景，揭示课题
目录
CONTENT
（一）复习回顾，创设情景，揭示课题
目录
CONTENT
（二）研讨新知，典型示例
目录
CONTENT
充分条件是唯一的吗？
一、充分条件
（1）所谓充分，就是说条件是充分的，也就是说条件是充足的，条件是足够的，只要有p一定有结论q，条件是足以保证的.“有之必成立，无之未必不成立”．
（2）充分条件不是唯一的，如果我是长沙人，那么我也是湖南人
对充分条件的理解
我是益阳人
我是湖南人
特别提醒：
1.的含义
（1）“若，则”形式的命题为真命题．
（2）由条件可以得到结论．
（3）是的充分条件或的充分条件是；
是的必要条件或的必要条件是．
（4）只要有条件，就一定有结论，即对于是充分的，对于的成立是必要的．
（5）为得到结论，具备条件即可．
显然，是的充分条件与是的必要条件表述的是同一个逻辑关系，即，只是说法不同而已．
二、必要条件
例1下列“若，则”形式的命题中，哪些命题中的是的必要条件？
（1）若一个四边形是等腰梯形，则这个四边形的两条对角线相等；
（2）若是直角三角形，则是等腰三角形；
（3）若，则；
（4）若关于的方程有唯一解，则．
[解析]（1）等腰梯形的两条对角线相等,因此，所以是的必要条件．
（2）直角三角形不一定是等腰三角形,因此，所以不是的必要条件．
（3）命题“若，则”是真命题，因此，所以是的必要条件．
（4）命题“若关于的方程有唯一解，则”为假命题，因此，所以不是的必要条件．
（1）所谓必要，如果q不成立，则p一定不成立，q对于p而言是必要的，没有q则p一定不成立，我是湖南人不成立，那么我一定不是益阳人
对必要条件的理解
我是益阳人
我是湖南人
（2）必要条件不是唯一的，如X>3，可以推出X>2，也可以推出X>1
例2下列“若，则”形式的命题中，哪些命题中的是的充分条件？
（1）若，则；
（2）若，则；
（3）若，，，则；
（4）若，则；
（5）在中，若，则；
（6）若四边形是正方形，则四边形是菱形.
方法总结 充分条件与必要条件的两种判断方法
（1）定义法：
（2）命题判断法：
若命题“若，则”是真命题，则p是q的充分条件，是的必要条件；若命题“若，则”是假命题，则p不是q的充分条件，不是的必要条件.
确定谁是p，谁是q
尝试由p推出q
若能推出，则p是q的充分条件，q是p的必要条件
记笔记
[解析]（1）因为，所以，所以是的充分条件．
（2）因为，所以.因此，所以是的充分条件．
（3）若，，则，但，所以，所以不是的充分条件．
（4）由可以推出或，不一定有，因此，所以不是的充分条件．
（5）由三角形中大角对大边可知，若，则，因此，所以是的充分条件．
（6）由菱形和正方形的定义可知，所有的正方形都是菱形，所以，所以是的充分条件．
方法总结 充分条件的两种判断方法
（1）定义法：
（2）命题判断法：
若命题“若，则”是真命题，则是的充分条件；若命题“若，则”是假命题，则不是的充分条件.
1.判断下列结论是否正确.（正确的打“√”，错误的打“×”）
（1）如果是的必要条件，那么是唯一的.()
×
（2）是的必要条件的含义是：如果不成立，那么一定不成立.()
√
（3）“”是“，都大于0”成立的充分条件.()
×
（4）若是的充分条件，则是的必要条件.()
√
1.设集合，，则“”是“”的_______条件.（填“充分”或“必要”）
必要
[解析]因为集合，，当时，.因为“”“”，但“”“”，所以“”是“”的必要条件．
2.设集合，，那么“”是“”的_______条件.（填“充分”或“必要”）
充分
[解析]由题意得，所以“”“”，所以“”是“”的充分条件.
已知 p：关于x的不等式 q：01.若p是q的充分条件，求实数m的取值范围，
2.p是q的必要条件求实数m的取值范围．
探究2 充要条件
若，则称是的充分条件，是的必要条件
若，则称p不是q的充分条件，q不是p的必要条件


且
呢？
新知生成
充要条件
（1）如果“若，则”和“若，则”均是真命题，即既有________，又有________，就记作_________.此时，既是的充分条件，也是的必要条件，我们说是的充分必要条件，简称为___________．



充要条件
（2）当是的充要条件时，也是的_______条件．
充要
（3）是的充要条件也常常说成“成立___________成立”或“与_______”．
当且仅当
等价
特别提醒：从概念的角度去理解充分条件、必要条件、充要条件
（1）若，则称是的充分条件，是的必要条件．
（2）若，则是的充要条件．
（3）若，且，则称是的充分不必要条件．
（4）若，且，则称是的必要不充分条件．
（5）若，且，则称是的既不充分也不必要条件．
新知运用
例3指出下列各题中，是的什么条件.（在“充分不必要条件”“必要不充分条件”“充要条件” “既不充分也不必要条件”中选出一种作答）
（1）在中，，.
（2）或，：方程有两个不同的实根.
（3）已知,,,.
[解析]（1）在中，显然有，是的充要条件.
（2）方程有两个不同的实根，且，且,
是的既不充分也不必要条件.
（3）,是的充要条件.
，中至少有一个不为零的充要条件是(@47@).
A.B.C.D.
D
[解析]若，则，不同时为零；若，中至少有一个不为零，则．故选D.
探究3 充要条件的证明
已知关于的方程有两个负实根的充要条件是.
问题1：.由得到方程有两个负实根，这个过程是“充分性”还是“必要性”？
[答案]充分性；是条件，方程有两个负实根是结论.
问题2：.由方程有两个负实根直接求解得到的取值范围，则的取值范围是方程有两个负实根的什么条件？
[答案] 必要条件.
问题3：.互为充要条件是指条件和结论是相对的，在充要条件问题的证明中，条件是确定的吗？
[答案] 互为充要条件中，条件和结论是相对的，在充要条件问题的证明中，条件是确定的.
新知生成
充要条件的证明一般分为两个步骤，即分别证明“充分性”和“必要性”这两个方面．解题时要避免将充分性当作必要性来证明，这就需要分清条件与结论，若“条件”“结论”，则是证明充分性，若“结论”“条件”，则是证明必要性．
新知运用
例4证明：一元二次方程有一个正实数根和一个负实数根的充要条件是.
结论q
条件p
求证：关于的方程有一个根是1的充要条件是．
1.若，则“”是“”的(@54@).
A.充分不必要条件B.必要不充分条件
C.既不充分也不必要条件D.充要条件
A
[解析]因为“”“”，而“”“”，所以“”是“”的充分不必要条件，故选．
2.“”是“”的(@56@).
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
B
[解析]，∴“”是“”的必要不充分条件.故选B.
3.函数的图象关于直线对称的充要条件是__________．

[解析]若函数的图象关于直线对称，则，即；反之，若，则函数的图象关于直线对称．
4.已知实数满足，其中；实数满足.若是的充分条件，求实数的取值范围．
3、充分条件、必要条件及充要条件之间有什么关系？
课堂小结