物理人教版(2019)必修第三册10.5 带电粒子在电场中的运动(共36张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第三册10.5 带电粒子在电场中的运动(共36张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-16 21:00:51 | ||
图片预览






文档简介
(共36张PPT)
10.5 带电粒子在电场中的运动
复习回顾:
1、高一我们重点研究过哪些运动形式?
(1)直线运动——匀速直线运动和匀变速直线运动
(2)曲线运动——平抛运动和匀速圆周运动
2、对这些运动形式的研究主要采用的哪些方法?
(1)动力学方法——牛顿定律和运动学公式
(2)能量方法——动能定理和能量守恒定律
3、不管用那种方法研究物体的运动必须做的是什么?
对研究对象做好受力分析
研究带电粒子运动的主要工具:
电场力
加速度
电场力的功
动能定理
F=qE
W=qU
一、研究对象与受力特征
1、研究对象
微观粒子:如电子、质子、各类离子等……
宏观粒子:液滴、小球、小物块、小环等……
2、受力特征
一般说来微观粒子及题目中强调不计重力的不必考虑重力,宏观粒子需要考虑重力。
当条件不明时,比较qE与mg大小,若qE>>mg,则不计重力。
注意:不计重力,不是不要考虑质量,求加速度要用a=F合/m。
带电粒子处于电场中
受电场力
产生加速度
改变运动状态
二、 带电粒子在电场中的加速
例题1:炽热的金属丝可以发射电子。在金属丝和金属板间加以电压U=2500V,发射出的电子在真空中加速后,从金属板的小孔穿出。电子穿出时的速度有多大?设电子刚离开金属丝时的速度为零,电子质量m=9×10-31kg。
E
问题1:电子受到几个力的作用?方向向哪?
问题2:电子哪个方向做什么运动?
问题3:可以用几种办法求解电子穿出时的速度?
3、方法:(1)动力学方法——牛顿定律和运动学公式
(2)能量方法——动能定理和能量守恒定律
1、受力分析:
水平向右的电场力 F=Eq=qU/d
2、运动分析:
初速度为零,加速度为a=qU/md的向右匀加速直线运动。
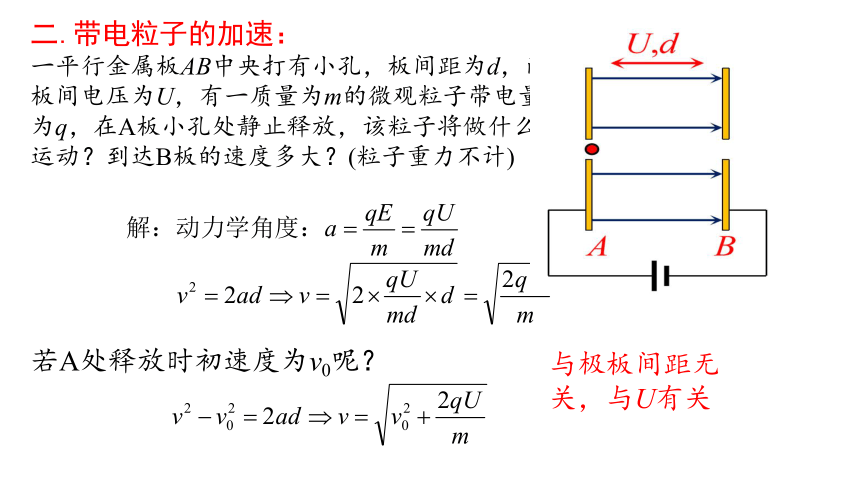
二.带电粒子的加速:
一平行金属板AB中央打有小孔,板间距为d,两板间电压为U,有一质量为m的微观粒子带电量为q,在A板小孔处静止释放,该粒子将做什么运动?到达B板的速度多大?(粒子重力不计)
若A处释放时初速度为v0呢?
v
与极板间距无关,与U有关
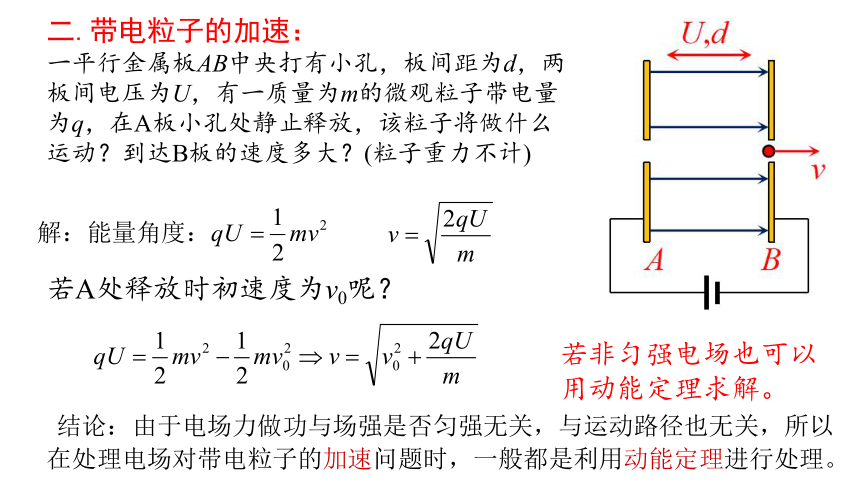
二.带电粒子的加速:
一平行金属板AB中央打有小孔,板间距为d,两板间电压为U,有一质量为m的微观粒子带电量为q,在A板小孔处静止释放,该粒子将做什么运动?到达B板的速度多大?(粒子重力不计)
若A处释放时初速度为v0呢?
若非匀强电场也可以用动能定理求解。
结论:由于电场力做功与场强是否匀强无关,与运动路径也无关,所以在处理电场对带电粒子的加速问题时,一般都是利用动能定理进行处理。
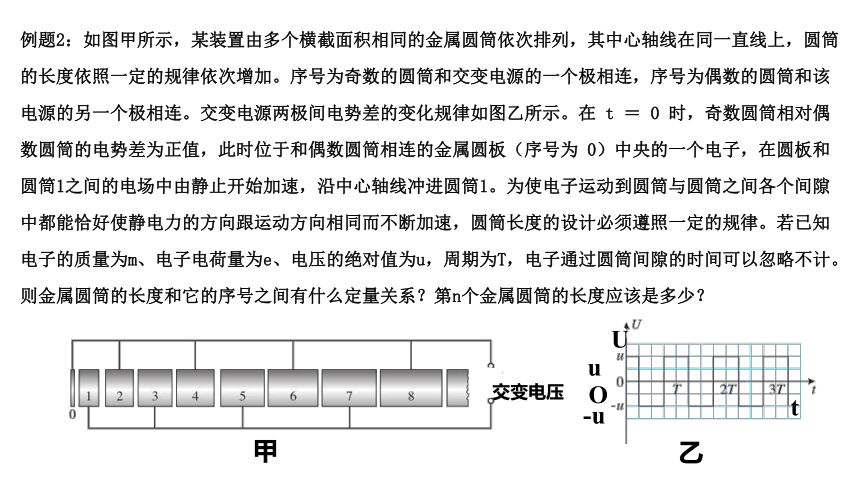
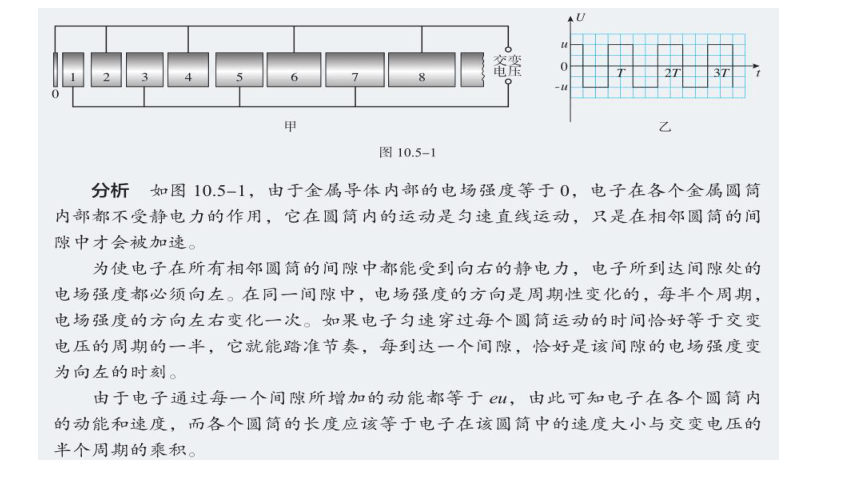
例题2:如图甲所示,某装置由多个横截面积相同的金属圆筒依次排列,其中心轴线在同一直线上,圆筒的长度依照一定的规律依次增加。序号为奇数的圆筒和交变电源的一个极相连,序号为偶数的圆筒和该电源的另一个极相连。交变电源两极间电势差的变化规律如图乙所示。在 t = 0 时,奇数圆筒相对偶数圆筒的电势差为正值,此时位于和偶数圆筒相连的金属圆板(序号为 0)中央的一个电子,在圆板和圆筒1之间的电场中由静止开始加速,沿中心轴线冲进圆筒1。为使电子运动到圆筒与圆筒之间各个间隙中都能恰好使静电力的方向跟运动方向相同而不断加速,圆筒长度的设计必须遵照一定的规律。若已知电子的质量为m、电子电荷量为e、电压的绝对值为u,周期为T,电子通过圆筒间隙的时间可以忽略不计。则金属圆筒的长度和它的序号之间有什么定量关系?第n个金属圆筒的长度应该是多少?
交变电压
U
t
u
O
-u
甲
乙
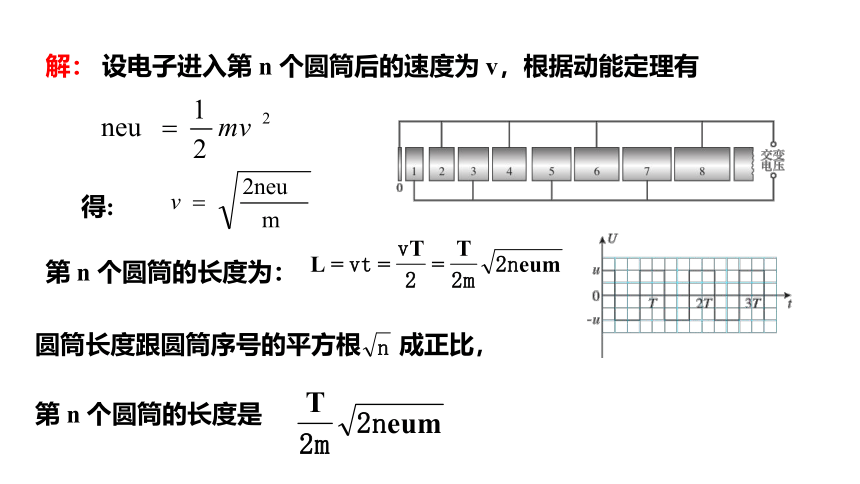
解: 设电子进入第 n 个圆筒后的速度为 v,根据动能定理有
圆筒长度跟圆筒序号的平方根 成正比,
第 n 个圆筒的长度是
得:
第 n 个圆筒的长度为:
三、 带电粒子在电场中的偏转
复习回顾:
1、平抛运动的特点:
只受重力,初速度方向水平,初速度方向与重力方向垂直,轨迹是一条抛物线,水平方向做匀速直线运动,竖直方向做自由落体运动
2、平抛运动速度规律公式:
O
x
y
v0
P (x,y)
α
vx = v0
vy
v
3、平抛运动位移规律公式:
O
x
y
P (x,y)
B
A
v0
4、平抛运动推论:
(1)位移偏向角θ与速度偏向角α的关系:
(2)速度方向的反向延长线与x轴的交点为水平位移的中点。
l
θ
m
+q
+
_
v0
你能画出带电微粒的运动轨迹吗?
探究:带电粒子的偏转规律
问题:
带电粒子的偏转:(不计重力)
+ + + + + + + + +
- - - - - - - - -
v0
+
q.m
d
l
F
+
θ
y
v
v0
vy
侧移
偏转角
1.运动状态分析:
带电粒子以速度v0垂直于电场线方向飞入两带电平行板产生的匀强电场时,若只受电场力作用,则带电粒子做匀变速曲线运动。
2.偏转问题的分析处理方法:(类似平抛运动分析方法)
(1)沿初速度方向是速度为v0的匀速直线运动;
(2)沿电场力方向是初速度为零的匀加速直线运动。
类平抛运动
与粒子比荷 成正比
与粒子初速度v0的平方成反比
与电场的属性U、l、d有关
与粒子比荷 成正比
与粒子初速度v0 的平方成反比
与电场的属性U、l、d有关
例2:如图一所示,一电荷量q,质量m的带正电的粒子以速度v0,沿中线垂直进入平行板间的匀强电场,上极板带正电,下极板带负电,若上下两板间电势差为U2,间距为d,极板长度为L1,求当粒子能从平行板间飞出时粒子的沿电场方向偏移距离y为多少?速度的偏转角θ为多少?
问题1:带电粒子在垂直电场方向和沿电场方向各受到怎样的力?带电粒子在这两个方向各做什么运动?
问题2:带电粒子的运动方式是否与平抛运动类似?
解:
垂直电场方向:
平行电场方向:
所以:
〖2020.1〗
第7题图
7.如图所示,电子以某一初速度沿两块平行板的中线方向射入偏转电场中,已知极板长度l,间距d,电子质量m,电荷量e。若电子恰好从极板边缘射出电场,由以上条件可以求出的是( )
A.偏转电压
B.偏转的角度
C.射出电场速度
D.电场中运动的时间
浙江高考真题练
B
【解析】根据推论,粒子速度方向的反向延长线交于其水平位移的中点,即
,因此粒子射出电场的偏转角度可求,选项B正确。
该式子中,初速度、电场强度都不知道,因此无法求出射出电场的速度,在电场中的运动时间,偏转电压,所以选项ACD均错误。
〖2020.7选〗 6.如图所示,一质量为m、电荷量为 q(q>0 )的粒子以速度 v0从 连线上的P点水平向右射入大小为E、方向竖直向下的匀强电场中。已知 与水平方向成45°角,粒子的重力可以忽略,则粒子到达 连线上的某点时( )
浙江高考真题练
A. 所用时间为
B. 速度大小为
C. 与P点的距离为
D. 速度方向与竖直方向的夹角为30°
C
〖2020.7选〗 6.如图所示,一质量为m、电荷量为 q(q>0 )的粒子以速度 v0从 连线上的P点水平向右射入大小为E、方向竖直向下的匀强电场中。已知 与水平方向成45°角,粒子的重力可以忽略,则粒子到达 连线上的某点时( )
浙江高考真题练
C
四、 带电粒子在电场中的加速和偏转一体
【拓展1】:若该粒子先经过一个电势差为U1加速度电场后,再进入电势差为U2的偏转电场,其他条件不变,求当粒子能从平行板间飞出时粒子的沿电场方向偏移距离y为多少?速度的偏转角θ为多少?
U1
+
+
+
+
+
+
-
-
-
-
-
-
+
_
U1
U2
v
-q
m
L
v0
加速
偏转
电荷经加速电场加速后进入偏转电场
通过加速电场的末速度为进入偏转电场的初速度
探究:带电粒子先加速再偏转的运动规律
结论:此种情况下,粒子的偏转位移、偏转角度与粒子无关。
方法一:
方法二:
【拓展2】:若该粒子先经过一个电势差为U1加速度电场后,再进入电势差为U2的偏转电场,偏出偏转电场后,粒子打在距离极板右侧为L2荧光屏上,其他条件不变,求当粒子从进入偏转电场到打在荧光屏上总共偏移距离Y为多少?
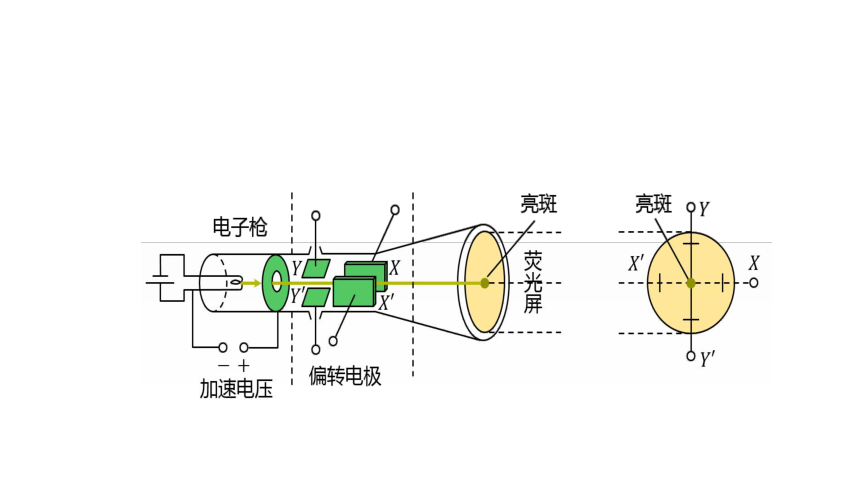
(1)电子枪:发射并加速电子。
(2)偏转电极:YY′使电子束竖直偏转;XX′使电子束水平偏转。
(3)荧光屏:电子束打到荧光屏上能使该处的荧光物质发光。
偏转电极
亮斑
亮斑
电子枪
加速电压
荧光屏
-
+
观察下图说出示波管的构造以及原理
拓展应用:
Y
Y’
X
X’
-
+
-
-
+
-
若金属平行板水平放置,电子将在竖直方向发生偏转
若金属平行板竖直放置,电子将在水平方向发生偏转
偏转电极的不同放置方式
Y
Y′
X′
YY′随信号电压同步变化,但由于视觉暂留和荧光物质的残光特性,只能看到一条竖直的亮线。
X
示波器图象
如果在XX′之间不加电压,而在YY′之间所加的电压按图所示的规律随时间变化,在荧光屏上会看到什么图形?
同理可得亮斑在水平方向的偏移随加在XX′上的电压而变化,若所加的电压为特定的周期性变化电压则亮斑在水平方向来回运动——扫描,如果扫描电压变化很快,亮斑看起来为一条水平的亮线。
UX
t
扫描电压
示波器图象
Y
Y′
X′
X
如果在YY′之间加如图所示的交变电压,同时在XX′之间加锯齿形扫描电压,在荧光屏上会看到什么图形?
X
Y
O
A
B
C
D
E
F
A
B
C
D
E
F
A
B
O
C
t1
D
E
F
t2
Uy
Ux
1.静电火箭是利用电场加速工作介质形成高速射流而产生推力的。工作过程简化图如图所示,离子源发射的带电离子经过加速区加速,进入中和区与该区域里面的电子中和,最后形成中性高速射流喷射而产生推力。根据题目信息可知( )
A.M板电势低于N板电势
B.进入中和区的离子速度与离子带电荷量无关
C.增大加速区MN极板的距离,可以增大射流速度而获得更大的推力
D.增大MN极板间的电压,可以增大射流速度而获得更大的推力
D
10.5 带电粒子在电场中的运动
复习回顾:
1、高一我们重点研究过哪些运动形式?
(1)直线运动——匀速直线运动和匀变速直线运动
(2)曲线运动——平抛运动和匀速圆周运动
2、对这些运动形式的研究主要采用的哪些方法?
(1)动力学方法——牛顿定律和运动学公式
(2)能量方法——动能定理和能量守恒定律
3、不管用那种方法研究物体的运动必须做的是什么?
对研究对象做好受力分析
研究带电粒子运动的主要工具:
电场力
加速度
电场力的功
动能定理
F=qE
W=qU
一、研究对象与受力特征
1、研究对象
微观粒子:如电子、质子、各类离子等……
宏观粒子:液滴、小球、小物块、小环等……
2、受力特征
一般说来微观粒子及题目中强调不计重力的不必考虑重力,宏观粒子需要考虑重力。
当条件不明时,比较qE与mg大小,若qE>>mg,则不计重力。
注意:不计重力,不是不要考虑质量,求加速度要用a=F合/m。
带电粒子处于电场中
受电场力
产生加速度
改变运动状态
二、 带电粒子在电场中的加速
例题1:炽热的金属丝可以发射电子。在金属丝和金属板间加以电压U=2500V,发射出的电子在真空中加速后,从金属板的小孔穿出。电子穿出时的速度有多大?设电子刚离开金属丝时的速度为零,电子质量m=9×10-31kg。
E
问题1:电子受到几个力的作用?方向向哪?
问题2:电子哪个方向做什么运动?
问题3:可以用几种办法求解电子穿出时的速度?
3、方法:(1)动力学方法——牛顿定律和运动学公式
(2)能量方法——动能定理和能量守恒定律
1、受力分析:
水平向右的电场力 F=Eq=qU/d
2、运动分析:
初速度为零,加速度为a=qU/md的向右匀加速直线运动。
二.带电粒子的加速:
一平行金属板AB中央打有小孔,板间距为d,两板间电压为U,有一质量为m的微观粒子带电量为q,在A板小孔处静止释放,该粒子将做什么运动?到达B板的速度多大?(粒子重力不计)
若A处释放时初速度为v0呢?
v
与极板间距无关,与U有关
二.带电粒子的加速:
一平行金属板AB中央打有小孔,板间距为d,两板间电压为U,有一质量为m的微观粒子带电量为q,在A板小孔处静止释放,该粒子将做什么运动?到达B板的速度多大?(粒子重力不计)
若A处释放时初速度为v0呢?
若非匀强电场也可以用动能定理求解。
结论:由于电场力做功与场强是否匀强无关,与运动路径也无关,所以在处理电场对带电粒子的加速问题时,一般都是利用动能定理进行处理。
例题2:如图甲所示,某装置由多个横截面积相同的金属圆筒依次排列,其中心轴线在同一直线上,圆筒的长度依照一定的规律依次增加。序号为奇数的圆筒和交变电源的一个极相连,序号为偶数的圆筒和该电源的另一个极相连。交变电源两极间电势差的变化规律如图乙所示。在 t = 0 时,奇数圆筒相对偶数圆筒的电势差为正值,此时位于和偶数圆筒相连的金属圆板(序号为 0)中央的一个电子,在圆板和圆筒1之间的电场中由静止开始加速,沿中心轴线冲进圆筒1。为使电子运动到圆筒与圆筒之间各个间隙中都能恰好使静电力的方向跟运动方向相同而不断加速,圆筒长度的设计必须遵照一定的规律。若已知电子的质量为m、电子电荷量为e、电压的绝对值为u,周期为T,电子通过圆筒间隙的时间可以忽略不计。则金属圆筒的长度和它的序号之间有什么定量关系?第n个金属圆筒的长度应该是多少?
交变电压
U
t
u
O
-u
甲
乙
解: 设电子进入第 n 个圆筒后的速度为 v,根据动能定理有
圆筒长度跟圆筒序号的平方根 成正比,
第 n 个圆筒的长度是
得:
第 n 个圆筒的长度为:
三、 带电粒子在电场中的偏转
复习回顾:
1、平抛运动的特点:
只受重力,初速度方向水平,初速度方向与重力方向垂直,轨迹是一条抛物线,水平方向做匀速直线运动,竖直方向做自由落体运动
2、平抛运动速度规律公式:
O
x
y
v0
P (x,y)
α
vx = v0
vy
v
3、平抛运动位移规律公式:
O
x
y
P (x,y)
B
A
v0
4、平抛运动推论:
(1)位移偏向角θ与速度偏向角α的关系:
(2)速度方向的反向延长线与x轴的交点为水平位移的中点。
l
θ
m
+q
+
_
v0
你能画出带电微粒的运动轨迹吗?
探究:带电粒子的偏转规律
问题:
带电粒子的偏转:(不计重力)
+ + + + + + + + +
- - - - - - - - -
v0
+
q.m
d
l
F
+
θ
y
v
v0
vy
侧移
偏转角
1.运动状态分析:
带电粒子以速度v0垂直于电场线方向飞入两带电平行板产生的匀强电场时,若只受电场力作用,则带电粒子做匀变速曲线运动。
2.偏转问题的分析处理方法:(类似平抛运动分析方法)
(1)沿初速度方向是速度为v0的匀速直线运动;
(2)沿电场力方向是初速度为零的匀加速直线运动。
类平抛运动
与粒子比荷 成正比
与粒子初速度v0的平方成反比
与电场的属性U、l、d有关
与粒子比荷 成正比
与粒子初速度v0 的平方成反比
与电场的属性U、l、d有关
例2:如图一所示,一电荷量q,质量m的带正电的粒子以速度v0,沿中线垂直进入平行板间的匀强电场,上极板带正电,下极板带负电,若上下两板间电势差为U2,间距为d,极板长度为L1,求当粒子能从平行板间飞出时粒子的沿电场方向偏移距离y为多少?速度的偏转角θ为多少?
问题1:带电粒子在垂直电场方向和沿电场方向各受到怎样的力?带电粒子在这两个方向各做什么运动?
问题2:带电粒子的运动方式是否与平抛运动类似?
解:
垂直电场方向:
平行电场方向:
所以:
〖2020.1〗
第7题图
7.如图所示,电子以某一初速度沿两块平行板的中线方向射入偏转电场中,已知极板长度l,间距d,电子质量m,电荷量e。若电子恰好从极板边缘射出电场,由以上条件可以求出的是( )
A.偏转电压
B.偏转的角度
C.射出电场速度
D.电场中运动的时间
浙江高考真题练
B
【解析】根据推论,粒子速度方向的反向延长线交于其水平位移的中点,即
,因此粒子射出电场的偏转角度可求,选项B正确。
该式子中,初速度、电场强度都不知道,因此无法求出射出电场的速度,在电场中的运动时间,偏转电压,所以选项ACD均错误。
〖2020.7选〗 6.如图所示,一质量为m、电荷量为 q(q>0 )的粒子以速度 v0从 连线上的P点水平向右射入大小为E、方向竖直向下的匀强电场中。已知 与水平方向成45°角,粒子的重力可以忽略,则粒子到达 连线上的某点时( )
浙江高考真题练
A. 所用时间为
B. 速度大小为
C. 与P点的距离为
D. 速度方向与竖直方向的夹角为30°
C
〖2020.7选〗 6.如图所示,一质量为m、电荷量为 q(q>0 )的粒子以速度 v0从 连线上的P点水平向右射入大小为E、方向竖直向下的匀强电场中。已知 与水平方向成45°角,粒子的重力可以忽略,则粒子到达 连线上的某点时( )
浙江高考真题练
C
四、 带电粒子在电场中的加速和偏转一体
【拓展1】:若该粒子先经过一个电势差为U1加速度电场后,再进入电势差为U2的偏转电场,其他条件不变,求当粒子能从平行板间飞出时粒子的沿电场方向偏移距离y为多少?速度的偏转角θ为多少?
U1
+
+
+
+
+
+
-
-
-
-
-
-
+
_
U1
U2
v
-q
m
L
v0
加速
偏转
电荷经加速电场加速后进入偏转电场
通过加速电场的末速度为进入偏转电场的初速度
探究:带电粒子先加速再偏转的运动规律
结论:此种情况下,粒子的偏转位移、偏转角度与粒子无关。
方法一:
方法二:
【拓展2】:若该粒子先经过一个电势差为U1加速度电场后,再进入电势差为U2的偏转电场,偏出偏转电场后,粒子打在距离极板右侧为L2荧光屏上,其他条件不变,求当粒子从进入偏转电场到打在荧光屏上总共偏移距离Y为多少?
(1)电子枪:发射并加速电子。
(2)偏转电极:YY′使电子束竖直偏转;XX′使电子束水平偏转。
(3)荧光屏:电子束打到荧光屏上能使该处的荧光物质发光。
偏转电极
亮斑
亮斑
电子枪
加速电压
荧光屏
-
+
观察下图说出示波管的构造以及原理
拓展应用:
Y
Y’
X
X’
-
+
-
-
+
-
若金属平行板水平放置,电子将在竖直方向发生偏转
若金属平行板竖直放置,电子将在水平方向发生偏转
偏转电极的不同放置方式
Y
Y′
X′
YY′随信号电压同步变化,但由于视觉暂留和荧光物质的残光特性,只能看到一条竖直的亮线。
X
示波器图象
如果在XX′之间不加电压,而在YY′之间所加的电压按图所示的规律随时间变化,在荧光屏上会看到什么图形?
同理可得亮斑在水平方向的偏移随加在XX′上的电压而变化,若所加的电压为特定的周期性变化电压则亮斑在水平方向来回运动——扫描,如果扫描电压变化很快,亮斑看起来为一条水平的亮线。
UX
t
扫描电压
示波器图象
Y
Y′
X′
X
如果在YY′之间加如图所示的交变电压,同时在XX′之间加锯齿形扫描电压,在荧光屏上会看到什么图形?
X
Y
O
A
B
C
D
E
F
A
B
C
D
E
F
A
B
O
C
t1
D
E
F
t2
Uy
Ux
1.静电火箭是利用电场加速工作介质形成高速射流而产生推力的。工作过程简化图如图所示,离子源发射的带电离子经过加速区加速,进入中和区与该区域里面的电子中和,最后形成中性高速射流喷射而产生推力。根据题目信息可知( )
A.M板电势低于N板电势
B.进入中和区的离子速度与离子带电荷量无关
C.增大加速区MN极板的距离,可以增大射流速度而获得更大的推力
D.增大MN极板间的电压,可以增大射流速度而获得更大的推力
D
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
