北师大版八年级上册数学 1.1.1探索勾股定理 教案
文档属性
| 名称 | 北师大版八年级上册数学 1.1.1探索勾股定理 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 628.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览



文档简介
《探索勾股定理》教学设计
——“数学核心素养”在数学教学中的运用
● 知识与技能目标
用数格子(或割、补、拼等)的办法体验勾股定理的探索过程并理解勾股定理反映的直角三角形的三边之间的数量关系,会初步运用勾股定理进行简单的计算和实际运用.
● 数学思考
让学生经历“观察—猜想—归纳—验证”的数学思想,并体会数形结合和特殊到一般的思想方法.
● 解决问题
进一步发展学生的说理和简单推理的意识及能力;进一步体会数学与现实生活的紧密联系.
● 情感与态度
在探索勾股定理的过程中,体验获得成功的快乐;通过介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习.
重点:掌握勾股定理并能利用它来解决实际问题。
难点:探索勾股定理。
一、聚焦问题
为了落实学生发展核心素养为宗旨,引导学生探索勾股定理定理,聚焦以下问题:
1.探索勾股定理.
2. 在勾股定理的探究活动中,引导学生体会割补法与数形结合思想的应用。
3.让学生从已有知识经验出发,从一般到特殊,再由特殊到一般,培养学生合情推理探索数学规律的数学思考能力;
4.在勾股定理的探究活动中,培养学生探究能力和合作精神;通过对勾股定理历史的了解,感受数学文化,增强爱国情感.
二、需要解决的核心问题
1.探索勾股定理
2. 在勾股定理的探究活动中,引导学生体会割补法与数形结合思想的应用。
三、核心分解问题
分解问题1:等腰直角三角形的三边向外作正方形,三个正方形的面积之间有什么关系?
分解问题2:一般直角三角形的三边向外作正方形,三个正方形的面积之间还有上述关系吗
分解问题3:对于所有的直角三角形都有这样的关系吗
四、教学过程
创设情境、引出课题
【问题引领】
教师引导学生以三角形边的数量关系:
任意一个三角形,三边的数量关系为: 等腰三角形 等边三角形
两边之和大于第三边,两边之差小于第三边 AB=AC AB=AC=BC
【活动探究】
当角特殊时,得到直角三角形:
此时三边的数量关系是什么呢?探讨这个问题,我们回到特殊三角形,等腰直角三角形:
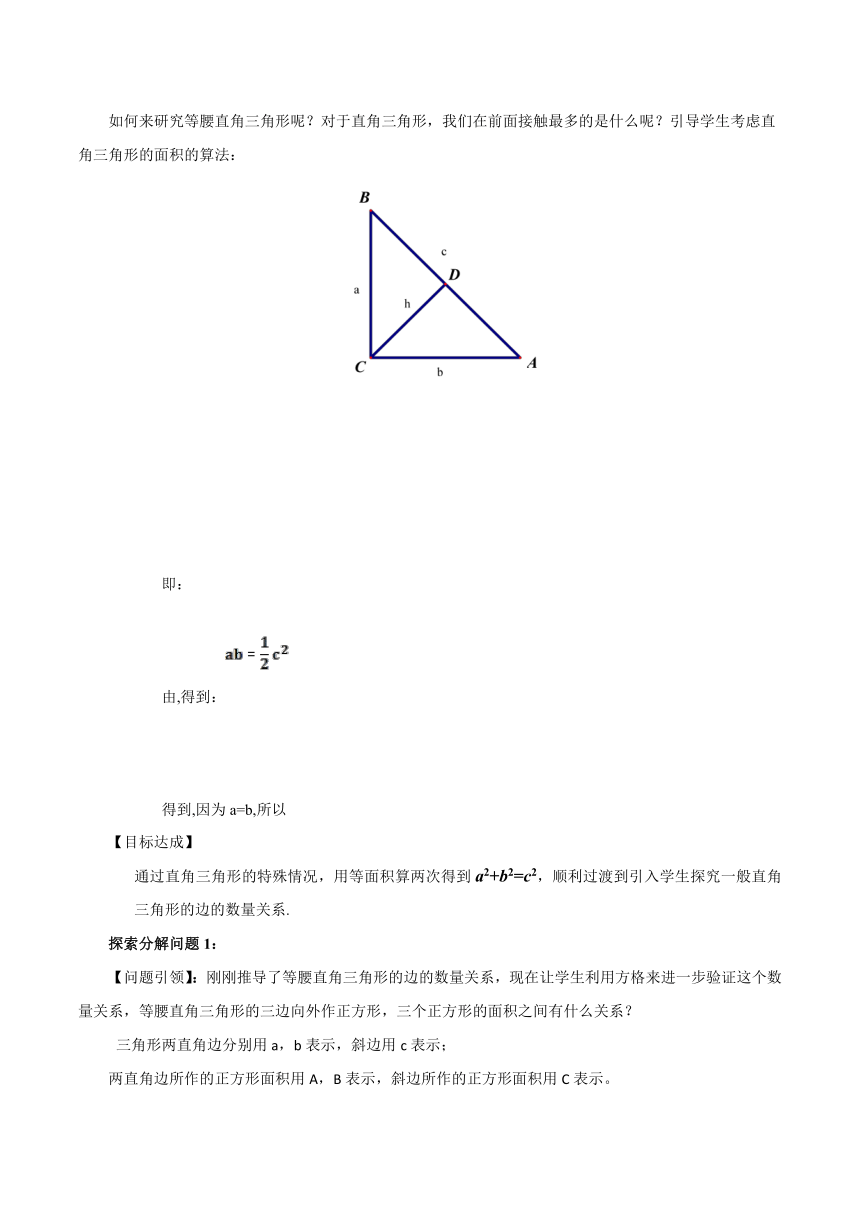
如何来研究等腰直角三角形呢?对于直角三角形,我们在前面接触最多的是什么呢?引导学生考虑直角三角形的面积的算法:
即:
由,得到:
得到,因为a=b,所以
【目标达成】
通过直角三角形的特殊情况,用等面积算两次得到a2+b2=c2,顺利过渡到引入学生探究一般直角三角形的边的数量关系.
探索分解问题1:
【问题引领】:刚刚推导了等腰直角三角形的边的数量关系,现在让学生利用方格来进一步验证这个数量关系,等腰直角三角形的三边向外作正方形,三个正方形的面积之间有什么关系?
三角形两直角边分别用a,b表示,斜边用c表示;
两直角边所作的正方形面积用A,B表示,斜边所作的正方形面积用C表示。
【活动探究】
1 让学生在方格纸上画等腰直角三角形,并以该三角形的三边向外作正方形,并想办法找出三个正方形面积A,B,C之间的关系,从而得出a2,b2,c2之间的关系;
2 收集各小组所作的图形集中作展示,引导学生思考不同边长的等腰直角三角形做出的图形三个面积A,B,C之间的关系有什么共同点
3 小组讨论,代表发言
【目标达成】
1 学生采用直接数方格的办法,(怎么数?)容易得到正方形A、B的面积,通过割补可得到面积C.
得到:面积A+面积B=面积C.即a2+b2=c2
2 提高学生动手能力和强化建模思想
探索分解问题2:
【问题引领】:一般直角三角形三边向外作正方形,三个正方形面积之间还有上述关系吗
【活动探究】
4 让学生在方格纸上画直角三角形,并以该三角形的三边向外作正方形,并想办法找出三个正方形面积A,B,C之间的关系,从而得出a2,b2,c2之间的关系;
5 收集各小组所作的图形集中作展示,引导学生思考不同边长的直角三角形做出的图形三个面积A,B,C之间的关系有什么共同点
6 小组讨论,代表发言
【目标达成】
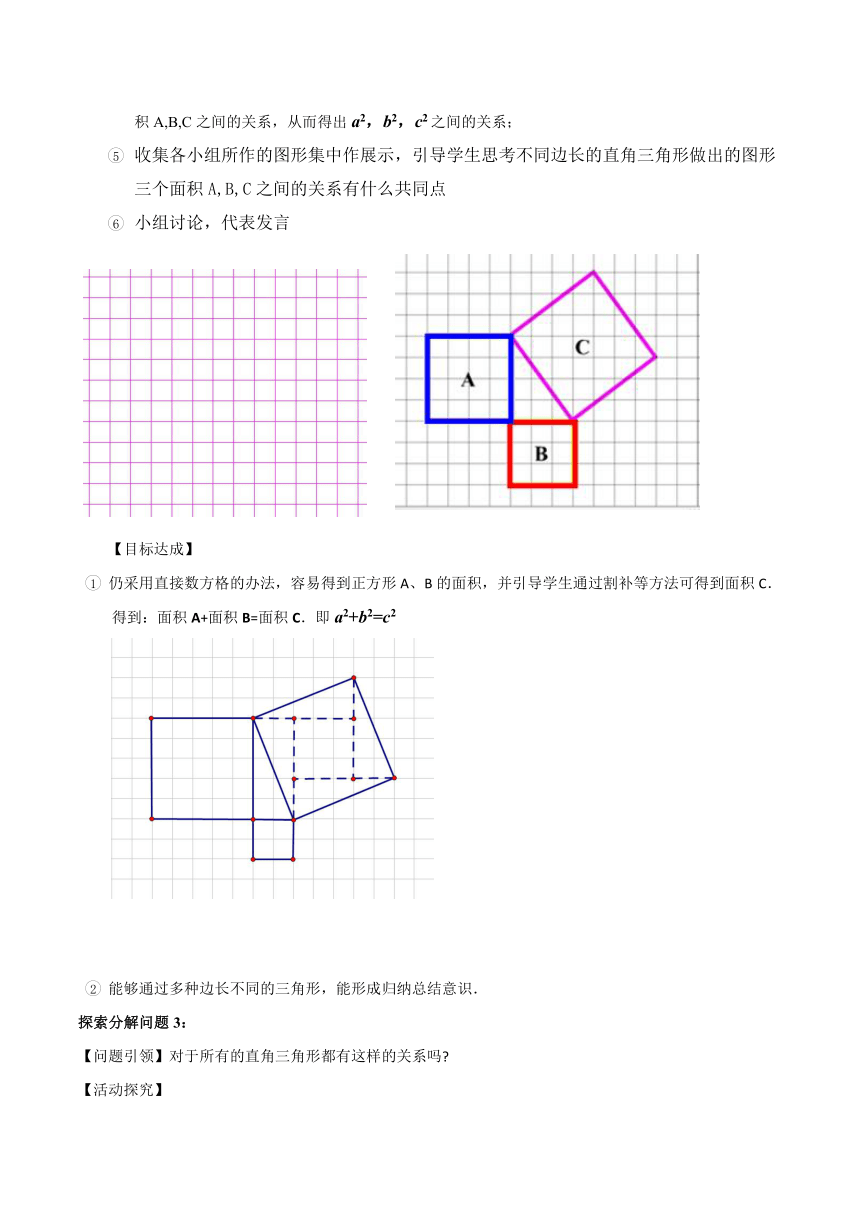
1 仍采用直接数方格的办法,容易得到正方形A、B的面积,并引导学生通过割补等方法可得到面积C.
得到:面积A+面积B=面积C.即a2+b2=c2
2 能够通过多种边长不同的三角形,能形成归纳总结意识.
探索分解问题3:
【问题引领】对于所有的直角三角形都有这样的关系吗
【活动探究】
教师几何画板演示多种不同边长的直角三角形,然后由学生操作,最后小组讨论,学生代表发言.
接着,各小组用分解2所得到的图形进行讨论,证明:
【目标达成】
1. 组长带领大家一起讨论,提出解决问题的办法;时间3分钟.
2 组长带着本组的想法跟其余组进行交流;时间2分钟.
3. 小组长回到自己的小组,和自己的组员整理出解决方案,并和大家分享解决办法.时间5分钟.
证明过程(本质上利用等面积方法,算两次进行等量代换):
即:
部分学生会有补全的证明:
即:
当然,学生还有其他很多证法,本节课重点介绍割补法的应用.
通过不同的情况总结得到只要是直角三角形,总有: a2+b2=c2(a,b为直角边,c为斜边),重难点得以突破.
【设计意图】本环节既是这节课的重点,也是这节课的难点.本环节安排了三个设问,从特殊到一般层层推进,既遵循了学生的认知规律,也体现了知识的发生、发展过程.在这个环节中,让学生观察、实验、交流,自主建构了知识的意义,同时发展了空间观念和推理能力.
归纳总结:引导学生总结勾股定理,并实现符号语言、文字语言和图形语言的互相转化.
勾股定理:
如果直角三角形两直角边为a,b斜边为c,那么
a2+b2=c2
即直角三角形两直角边的平方和等于斜边的平方.
【归纳过程】
1 教师引导学生总结勾股定理,并尝试转化为符号语言,文字语言和图形语言
2 教师对学生整理出的三种语言进行规范化总结
【目标达成】
1 学生掌握勾股定理的符号语言、文字语言和图形语言的准确表达和书写
定理理解与应用:如何利用勾股定理解题
1.快速计算下列直角三角形的第三边长:
【习题探究】
如图,已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
学生小组讨论总结运用勾股定理解决解直角三角形的方法,代表发言
【目标达成】.
1 及时反馈、及时巩固,同时培养学生应用数学的意识和能力
2 在直角三角形中,已知两边,会求第三边
③ 将翻折问题展现给学生,结合轴对称图形的性质,并将勾股定理作为解题的工具介绍给学生,让学生感受勾股定理的用途.
课堂小结布置作业
知识内容小结:
勾股定理:如果直角三角形两直角边分别为a ,b 斜边为c,那么
a2+b2=c2
问题解决:在直角三角形中,已知两边,会求第三边.
探索方法小结:
探索勾股定理的方法:从一般到特殊,再从特殊到一般,最后又从特殊到一般,归纳,总结。
思想方法小结:
1.建模思想:实际问题---- 建立模型(a2+b2=c2)----解决问题;
2.面积割补法;
3.数形结合思想.
【设计意图】在分组讨论的基础上,引导学生从知识和方法两个层面进行小结.知识小结有利于新知识条理化、简洁化,并将纳入学生原有的图形与公式的数学认知体系中;方法小结则突破当前的知识层面,带领学生站在更高的角度来理解数学知识,领悟数学的思想和方法
课外拓展:勾股定理的丰厚文化底蕴及历史探索历程
史料介绍:中国在勾股定理方面的成就
“我国在勾股定理方面的成就”:用图2验证勾股定理的方法,据载最早是三国时期数学家赵爽在为《周髀算经》作注时给出的,我国历史上将图2弦上的正方形称为弦图 .2002年的数学家大会(ICM-2002)在北京召开,这届大会会标的中央图案正是经过艺术处理的弦图,这既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!
中国勾股定理发展简史:
公元前十一世纪,周朝数学家商高就提出“勾三、股四、弦五”。《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”意为:当直角三角形的两条直角边分别为3(勾)和4(股)时,径隅(弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”,根据该典故称勾股定理为商高定理。
公元三世纪,三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释,记录于《九章算术》中“勾股各自乘,并而开方除之,即弦”,赵爽创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明。后刘徽在刘徽注中亦证明了勾股定理。
在中国清朝末年,数学家华蘅芳提出了二十多种对于勾股定理证法。
【设计意图】:
(1)介绍与勾股定理有关的历史,激发学生的爱国热情;
(2)学生加强了对中国数学史的了解,培养学习数学的兴趣激发爱国情感;
国际方面在勾股定理方面的成就
在公元前约三千年的古巴比伦人就知道和应用勾股定理,他们还知道许多勾股数组。美国哥伦比亚大学图书馆内收藏着一块编号为“普林顿322”的古巴比伦泥板,上面就记载了很多勾股数。古埃及人在建筑宏伟的金字塔和测量尼罗河泛滥后的土地时,也应用过勾股定理。
公元前六世纪,希腊数学家毕达哥拉斯证明了勾股定理,因而西方人都习惯地称这个定理为毕达哥拉斯定理。
公元前4世纪,希腊数学家欧几里得在《几何原本》(第Ⅰ卷,命题47)中给出一个证明。
1876年4月1日,加菲尔德在《新英格兰教育日志》上发表了他对勾股定理的一个证法。
1940年《毕达哥拉斯命题》出版,收集了367种不同的证法。
勾股定理与第一次数学危机.
约公元前500年,毕达哥拉斯学派的弟子希帕索斯(Hippasus)发现了一个惊人的事实,一个正方形的对角线的长度是不可公度的.按照毕达哥拉斯定理(勾股定理),若正方形边长是1,则对角线的长不是一个有理数,它不能表示成两个整数之比,这一事实不但与毕氏学派的哲学信念大相径庭,而且建立在任何两个线段都可以公度基础上的几何学面临被推翻的威胁,第一次数学危机由此爆发.据说,毕达哥拉斯学派对希帕索斯的发现十分惶恐、恼怒,为了保守秘密,最后将希帕索斯投入大海。第一次数学危机一直持续到19世纪实数的基础建立以后才圆满解决.我们将在下一章学习有关实数的知识.
作业:收集整理其他证明或验证勾股定理的方法。
c
a
bbb
——“数学核心素养”在数学教学中的运用
● 知识与技能目标
用数格子(或割、补、拼等)的办法体验勾股定理的探索过程并理解勾股定理反映的直角三角形的三边之间的数量关系,会初步运用勾股定理进行简单的计算和实际运用.
● 数学思考
让学生经历“观察—猜想—归纳—验证”的数学思想,并体会数形结合和特殊到一般的思想方法.
● 解决问题
进一步发展学生的说理和简单推理的意识及能力;进一步体会数学与现实生活的紧密联系.
● 情感与态度
在探索勾股定理的过程中,体验获得成功的快乐;通过介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习.
重点:掌握勾股定理并能利用它来解决实际问题。
难点:探索勾股定理。
一、聚焦问题
为了落实学生发展核心素养为宗旨,引导学生探索勾股定理定理,聚焦以下问题:
1.探索勾股定理.
2. 在勾股定理的探究活动中,引导学生体会割补法与数形结合思想的应用。
3.让学生从已有知识经验出发,从一般到特殊,再由特殊到一般,培养学生合情推理探索数学规律的数学思考能力;
4.在勾股定理的探究活动中,培养学生探究能力和合作精神;通过对勾股定理历史的了解,感受数学文化,增强爱国情感.
二、需要解决的核心问题
1.探索勾股定理
2. 在勾股定理的探究活动中,引导学生体会割补法与数形结合思想的应用。
三、核心分解问题
分解问题1:等腰直角三角形的三边向外作正方形,三个正方形的面积之间有什么关系?
分解问题2:一般直角三角形的三边向外作正方形,三个正方形的面积之间还有上述关系吗
分解问题3:对于所有的直角三角形都有这样的关系吗
四、教学过程
创设情境、引出课题
【问题引领】
教师引导学生以三角形边的数量关系:
任意一个三角形,三边的数量关系为: 等腰三角形 等边三角形
两边之和大于第三边,两边之差小于第三边 AB=AC AB=AC=BC
【活动探究】
当角特殊时,得到直角三角形:
此时三边的数量关系是什么呢?探讨这个问题,我们回到特殊三角形,等腰直角三角形:
如何来研究等腰直角三角形呢?对于直角三角形,我们在前面接触最多的是什么呢?引导学生考虑直角三角形的面积的算法:
即:
由,得到:
得到,因为a=b,所以
【目标达成】
通过直角三角形的特殊情况,用等面积算两次得到a2+b2=c2,顺利过渡到引入学生探究一般直角三角形的边的数量关系.
探索分解问题1:
【问题引领】:刚刚推导了等腰直角三角形的边的数量关系,现在让学生利用方格来进一步验证这个数量关系,等腰直角三角形的三边向外作正方形,三个正方形的面积之间有什么关系?
三角形两直角边分别用a,b表示,斜边用c表示;
两直角边所作的正方形面积用A,B表示,斜边所作的正方形面积用C表示。
【活动探究】
1 让学生在方格纸上画等腰直角三角形,并以该三角形的三边向外作正方形,并想办法找出三个正方形面积A,B,C之间的关系,从而得出a2,b2,c2之间的关系;
2 收集各小组所作的图形集中作展示,引导学生思考不同边长的等腰直角三角形做出的图形三个面积A,B,C之间的关系有什么共同点
3 小组讨论,代表发言
【目标达成】
1 学生采用直接数方格的办法,(怎么数?)容易得到正方形A、B的面积,通过割补可得到面积C.
得到:面积A+面积B=面积C.即a2+b2=c2
2 提高学生动手能力和强化建模思想
探索分解问题2:
【问题引领】:一般直角三角形三边向外作正方形,三个正方形面积之间还有上述关系吗
【活动探究】
4 让学生在方格纸上画直角三角形,并以该三角形的三边向外作正方形,并想办法找出三个正方形面积A,B,C之间的关系,从而得出a2,b2,c2之间的关系;
5 收集各小组所作的图形集中作展示,引导学生思考不同边长的直角三角形做出的图形三个面积A,B,C之间的关系有什么共同点
6 小组讨论,代表发言
【目标达成】
1 仍采用直接数方格的办法,容易得到正方形A、B的面积,并引导学生通过割补等方法可得到面积C.
得到:面积A+面积B=面积C.即a2+b2=c2
2 能够通过多种边长不同的三角形,能形成归纳总结意识.
探索分解问题3:
【问题引领】对于所有的直角三角形都有这样的关系吗
【活动探究】
教师几何画板演示多种不同边长的直角三角形,然后由学生操作,最后小组讨论,学生代表发言.
接着,各小组用分解2所得到的图形进行讨论,证明:
【目标达成】
1. 组长带领大家一起讨论,提出解决问题的办法;时间3分钟.
2 组长带着本组的想法跟其余组进行交流;时间2分钟.
3. 小组长回到自己的小组,和自己的组员整理出解决方案,并和大家分享解决办法.时间5分钟.
证明过程(本质上利用等面积方法,算两次进行等量代换):
即:
部分学生会有补全的证明:
即:
当然,学生还有其他很多证法,本节课重点介绍割补法的应用.
通过不同的情况总结得到只要是直角三角形,总有: a2+b2=c2(a,b为直角边,c为斜边),重难点得以突破.
【设计意图】本环节既是这节课的重点,也是这节课的难点.本环节安排了三个设问,从特殊到一般层层推进,既遵循了学生的认知规律,也体现了知识的发生、发展过程.在这个环节中,让学生观察、实验、交流,自主建构了知识的意义,同时发展了空间观念和推理能力.
归纳总结:引导学生总结勾股定理,并实现符号语言、文字语言和图形语言的互相转化.
勾股定理:
如果直角三角形两直角边为a,b斜边为c,那么
a2+b2=c2
即直角三角形两直角边的平方和等于斜边的平方.
【归纳过程】
1 教师引导学生总结勾股定理,并尝试转化为符号语言,文字语言和图形语言
2 教师对学生整理出的三种语言进行规范化总结
【目标达成】
1 学生掌握勾股定理的符号语言、文字语言和图形语言的准确表达和书写
定理理解与应用:如何利用勾股定理解题
1.快速计算下列直角三角形的第三边长:
【习题探究】
如图,已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
学生小组讨论总结运用勾股定理解决解直角三角形的方法,代表发言
【目标达成】.
1 及时反馈、及时巩固,同时培养学生应用数学的意识和能力
2 在直角三角形中,已知两边,会求第三边
③ 将翻折问题展现给学生,结合轴对称图形的性质,并将勾股定理作为解题的工具介绍给学生,让学生感受勾股定理的用途.
课堂小结布置作业
知识内容小结:
勾股定理:如果直角三角形两直角边分别为a ,b 斜边为c,那么
a2+b2=c2
问题解决:在直角三角形中,已知两边,会求第三边.
探索方法小结:
探索勾股定理的方法:从一般到特殊,再从特殊到一般,最后又从特殊到一般,归纳,总结。
思想方法小结:
1.建模思想:实际问题---- 建立模型(a2+b2=c2)----解决问题;
2.面积割补法;
3.数形结合思想.
【设计意图】在分组讨论的基础上,引导学生从知识和方法两个层面进行小结.知识小结有利于新知识条理化、简洁化,并将纳入学生原有的图形与公式的数学认知体系中;方法小结则突破当前的知识层面,带领学生站在更高的角度来理解数学知识,领悟数学的思想和方法
课外拓展:勾股定理的丰厚文化底蕴及历史探索历程
史料介绍:中国在勾股定理方面的成就
“我国在勾股定理方面的成就”:用图2验证勾股定理的方法,据载最早是三国时期数学家赵爽在为《周髀算经》作注时给出的,我国历史上将图2弦上的正方形称为弦图 .2002年的数学家大会(ICM-2002)在北京召开,这届大会会标的中央图案正是经过艺术处理的弦图,这既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!
中国勾股定理发展简史:
公元前十一世纪,周朝数学家商高就提出“勾三、股四、弦五”。《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”意为:当直角三角形的两条直角边分别为3(勾)和4(股)时,径隅(弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”,根据该典故称勾股定理为商高定理。
公元三世纪,三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释,记录于《九章算术》中“勾股各自乘,并而开方除之,即弦”,赵爽创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明。后刘徽在刘徽注中亦证明了勾股定理。
在中国清朝末年,数学家华蘅芳提出了二十多种对于勾股定理证法。
【设计意图】:
(1)介绍与勾股定理有关的历史,激发学生的爱国热情;
(2)学生加强了对中国数学史的了解,培养学习数学的兴趣激发爱国情感;
国际方面在勾股定理方面的成就
在公元前约三千年的古巴比伦人就知道和应用勾股定理,他们还知道许多勾股数组。美国哥伦比亚大学图书馆内收藏着一块编号为“普林顿322”的古巴比伦泥板,上面就记载了很多勾股数。古埃及人在建筑宏伟的金字塔和测量尼罗河泛滥后的土地时,也应用过勾股定理。
公元前六世纪,希腊数学家毕达哥拉斯证明了勾股定理,因而西方人都习惯地称这个定理为毕达哥拉斯定理。
公元前4世纪,希腊数学家欧几里得在《几何原本》(第Ⅰ卷,命题47)中给出一个证明。
1876年4月1日,加菲尔德在《新英格兰教育日志》上发表了他对勾股定理的一个证法。
1940年《毕达哥拉斯命题》出版,收集了367种不同的证法。
勾股定理与第一次数学危机.
约公元前500年,毕达哥拉斯学派的弟子希帕索斯(Hippasus)发现了一个惊人的事实,一个正方形的对角线的长度是不可公度的.按照毕达哥拉斯定理(勾股定理),若正方形边长是1,则对角线的长不是一个有理数,它不能表示成两个整数之比,这一事实不但与毕氏学派的哲学信念大相径庭,而且建立在任何两个线段都可以公度基础上的几何学面临被推翻的威胁,第一次数学危机由此爆发.据说,毕达哥拉斯学派对希帕索斯的发现十分惶恐、恼怒,为了保守秘密,最后将希帕索斯投入大海。第一次数学危机一直持续到19世纪实数的基础建立以后才圆满解决.我们将在下一章学习有关实数的知识.
作业:收集整理其他证明或验证勾股定理的方法。
c
a
bbb
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
