人教B版(2019)数学必修第三册 7_3_4正切函数的性质与图像课件(共42张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第三册 7_3_4正切函数的性质与图像课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 00:00:00 | ||
图片预览











文档简介
(共42张PPT)
正切函数的性质与图像
高一必修第三册
1.了解正切函数图像的画法,理解掌握正切函数的性质.
2.能利用正切函数的图像及性质解决有关问题.
本节目标
课前预习
(1)正切函数有哪些性质?
(2)正切函数在定义域内是不是单调函数?
预习课本,思考并完成以下问题
课前小测
1.在下列函数中同时满足:①在上递增;②以2π为周期;③是奇函数的是( )
A.y=tan x B.y=cos x
C.y=tan D.y=-tan x
C
周期为π
×
周期为π
×
在上递减
×
√
2.函数y=tan的定义域为___________________.
≠ k
,k∈Z
≠
,k∈Z
{x| ≠ ,k∈Z }
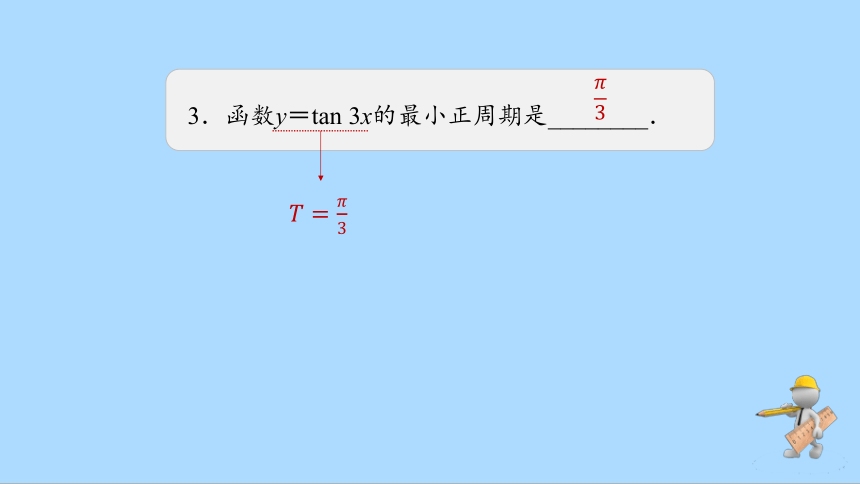
3.函数y=tan 3x的最小正周期是________.
4.函数y=tan 的单调增区间是_____________________.
,k∈Z
,k∈Z
,k∈Z
新知探究
正切函数的图像与性质
奇函数
(,0),k∈Z
题型突破
典例深度剖析 重点多维探究
题型一 有关正切函数的定义域、值域问题
[例1] (1) 函数y= 的值域是( )
A.(-1, 1) B.(-∞,-1)∪(1,+∞)
C.(-∞,1) D.(-1,+∞)
当-<x<0时,-1<tan x<0,∴ ≤-1;
当0<x< 时,0<tan x<1,∴ ≥1.
即当x∈(-,0)∪(0, )时,函数y= 的值域是(-∞,-1)∪(1,+∞).
B
(2) 函数y=3tan()的定义域为_______________________.
要使函数有意义应满足≠ kπ+,k∈Z,得x≠-4kπ- ,k∈Z,
所以函数的定义域为{x| x≠-4kπ- ,k∈Z}.
{x| x≠-4kπ- ,k∈Z}
(3)函数y= +lg(1-tan x)的定义域为_____________________________.
≥ 0
1-tan x>0
-1≤<1
在(- )上满足上述不等式的x的取值范围是[- ).
又因为y=tan x的周期为π,
所以所求x的定义域为
(1)求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数y=tan x有意义即x≠ +kπ,k∈Z.
技法点拨
求正切函数定义域的方法
(2)求正切型函数y=Atan(ωx+φ)(A≠0,ω>0)的定义域时,要将“ωx+φ”视为一个“整体”.令ωx+φ≠kπ+,k∈Z,解得x.
技法点拨
解形如tan x>a的不等式的步骤
易错提醒:求定义域时,要注意正切函数自身的限制条件.
跟踪训练
1.函数y= 的定义域是( )
A. {x|x = k , k∈Z} B. {x| kC. {x|x ≠ k , k∈Z} D. {x|x ≠ k , k∈Z}
B
>0
< 0
<
<
, k∈Z
2.求函数y=tan2 +tan+1的定义域和值域.
由3x+≠ kπ+,k∈Z,得x≠ + (k∈Z),
所以函数的定义域为{x| x≠ + (k∈Z)}.
设t=tan,
则t∈R,y=t2+t+1= 2+ ≥ ,
所以原函数的值域是[,+∞).
题型二 正切函数奇偶性、周期性和图像的对称性
[例2] (1)函数f(x)=tan 的周期为________.
(2)已知函数y=tan ,则该函数图像的对称中心坐标为________.
(3)判断下列函数的奇偶性:
①y=3xtan 2x-2x4; ②y=cos+tan x.
[例2] (1)函数f(x)=tan 的周期为________.
∵tan =tan ,
即tan =tan ,
∴f(x)=tan 的周期是.
法一:(定义法)
法二:(公式法)
f(x)=tan 的周期T= .
[例2] (2)已知函数y=tan ,则该函数图像的对称中心坐标为_______________.
所以图像的对称中心坐标为(+ ,0),k∈Z.
由x- = (k∈Z)得x= + (k∈Z),
(+ , 0),k∈Z
②y=cos+tan x.
[例2] (3)判断下列函数的奇偶性:
①y=3xtan 2x-2x4;
又f(-x)=3(-x)tan 2(-x)-2(-x)4=3xtan 2x-2x4=f(x),
定义域为{x|x≠ + , k∈Z},
关于原点对称,
所以它是偶函数.
定义域为{x|x≠+ , k∈Z} ,
关于原点对称,
y=cos()+tan x=sin x+tan x,
又f(-x)=sin(-x)+tan(-x)=-sin x-tan x=-f(x),
所以它是奇函数.
(3)观察法(或图像法):观察函数的图像,看自变量间隔多少,函数值重复出现.
函数f(x)=Atan(ωx+φ)周期的求解方法
(1)定义法.
(2)公式法:对于函数f(x)=Atan(ωx+φ)的最小正周期T= .
方法总结
先求函数的定义域,看其定义域是否关于原点对称,
若其不关于原点对称,则该函数为非奇非偶函数;
若其关于原点对称,再看f(-x)与f(x)的关系.
判定与正切函数有关的函数奇偶性的方法
提醒:y=tan x,x≠kπ+ ,k∈Z的对称中心坐标为(,0),k∈Z.
方法总结
跟踪训练
(1) f(x)= ;
(2) f(x)=tan +tan .
3.判断下列函数的奇偶性
(1) f(x)= ;
3.判断下列函数的奇偶性
f(x)的定义域为{x|x≠+ 且x≠+ , k∈Z},
所以函数f(x)既不是偶函数,也不是奇函数.
不关于原点对称,
由
x≠+ , k∈Z
1
得
(2) f(x)=tan +tan .
3.判断下列函数的奇偶性
函数定义域为{x|x≠且x≠+ , k∈Z},
关于原点对称,
又f(-x)=tan +tan
=-tan -tan
=-f(x),
所以函数f(x)是奇函数.
题型三 正切函数单调性的应用
1.正切函数y=tan x在其定义域内是否为增函数?
提示:不是.正切函数的图像被直线x=kπ+(k∈Z)隔开,所以它的单调区间只在(kπ, kπ+)(k∈Z)内,而不能说它在定义域内是增函数.假设x1=,x2= π,x1[探究问题]
2.如果让你比较tan()与tan ()的大小,你应该怎样做?
提示:先根据正切函数的周期性把两角化到同一单调区间内,再由正切函数的单调性进行比较.
[探究问题]
[例3] (1) tan 1,tan 2,tan 3,tan 4从小到大的排列顺序为________________________.
y=tan x在区间(, )上是单调增函数,且tan 1=tan(π+1),
所以tan 2<tan 3<tan 4<tan 1.
又<2<3<4<π+1< ,
tan 2<tan 3<tan 4<tan 1
[例3] (2)求函数y=3tan 的单调区间.
y=3tan =-3tan ,
由-+kπ<2x-<+kπ,k∈Z得,
-+ π<x< + π,k∈Z,
所以y=3tan 的减区间为(-+π,+π),k∈Z.
多维探究
变式1 求函数y=3tan 的单调区间.
由kπ-< x-得2kπ-∴函数y=3tan的单调递增区间是(2kπ-,2kπ+ π)(k∈Z).
变式2 求函数y=lgtan的单调区间.
因为函数y=lg x在(0,+∞)上为增函数.
所以函数y=lgtan x的单调递增区间就是函数y=tan x(tan x>0)的递增区间,
即(kπ, +kπ),k∈Z.
(2)若ω<0,可利用诱导公式先把y=Atan(ωx+φ)转化为y=Atan[-(-ωx-φ)]=-Atan(-ωx-φ),即把x的系数化为正值,再利用“整体代换”的思想,求得x的范围即可.
求函数y=Atan(ωx+φ)(A>0,ω≠0,且A,ω,φ都是常数)的单调区间的方法
(1)若ω>0,由于y=tan x在每一个单调区间上都是增函数,故可用“整体代换”的思想,令kπ-<ωx+φ<kπ+ ,k∈Z,解得x的范围即可.
方法总结
易错提醒:y=Atan(ωx+φ)(A>0,ω>0)只有增区间;y=Atan(ωx+φ)(A<0,ω>0)只有减区间.
运用正切函数单调性比较大小的步骤
(1)运用函数的周期性或诱导公式将角化到同一单调区间内.
(2)运用单调性比较大小关系.
方法总结
随堂检测
1.思考辨析
(1)正切函数的定义域和值域都是R.( )
(2)正切函数图像是中心对称图形,有无数个对称中心.( )
(3)正切函数图像有无数条对称轴,其对称轴是x=kπ±,k∈Z.( )
(4)正切函数是增函数.( )
×
√
×
×
2.若tan x≥1,则( )
A.2kπ-<x<2kπ(k∈Z)
B.x≤(2k+1)π(k∈Z)
C.kπ-<x≤kπ(k∈Z)
D.kπ+ ≤x<kπ+ (k∈Z)
D
3.求函数y=tan(π-x),x∈(-, )的值域为__________.
所以值域为(- ,1).
y=tan(π-x)=-tan x,
在(-, )上为减函数,
(- ,1)
4.求函数y=tan 的定义域、最小正周期、单调区间及其图像的对称中心.
②T= =2π,∴函数的最小正周期为2π.
①由≠kπ+ ,k∈Z,得x≠2kπ+ ,k∈Z,
∴函数的定义域为{x|x≠ 2kπ+ ,k∈Z}.
④由=,k∈Z,得x=kπ+,k∈Z,
∴函数图像的对称中心是(kπ+,0),k∈Z.
③由kπ-< <kπ+,k∈Z,得2kπ-<x<2kπ+,k∈Z,
∴函数的单调递增区间为(2kπ-, 2kπ+), k∈Z.
1.利用单位圆中的正切线作正切函数的图像,作图较为准确,但画图时较繁,我们常用“三点两线”法作正切曲线的简图.
本课小结
2.正切函数与正弦函数、余弦函数的性质比较.
本课小结
通过本节课,你学会了什么?
正切函数的性质与图像
高一必修第三册
1.了解正切函数图像的画法,理解掌握正切函数的性质.
2.能利用正切函数的图像及性质解决有关问题.
本节目标
课前预习
(1)正切函数有哪些性质?
(2)正切函数在定义域内是不是单调函数?
预习课本,思考并完成以下问题
课前小测
1.在下列函数中同时满足:①在上递增;②以2π为周期;③是奇函数的是( )
A.y=tan x B.y=cos x
C.y=tan D.y=-tan x
C
周期为π
×
周期为π
×
在上递减
×
√
2.函数y=tan的定义域为___________________.
≠ k
,k∈Z
≠
,k∈Z
{x| ≠ ,k∈Z }
3.函数y=tan 3x的最小正周期是________.
4.函数y=tan 的单调增区间是_____________________.
,k∈Z
,k∈Z
,k∈Z
新知探究
正切函数的图像与性质
奇函数
(,0),k∈Z
题型突破
典例深度剖析 重点多维探究
题型一 有关正切函数的定义域、值域问题
[例1] (1) 函数y= 的值域是( )
A.(-1, 1) B.(-∞,-1)∪(1,+∞)
C.(-∞,1) D.(-1,+∞)
当-<x<0时,-1<tan x<0,∴ ≤-1;
当0<x< 时,0<tan x<1,∴ ≥1.
即当x∈(-,0)∪(0, )时,函数y= 的值域是(-∞,-1)∪(1,+∞).
B
(2) 函数y=3tan()的定义域为_______________________.
要使函数有意义应满足≠ kπ+,k∈Z,得x≠-4kπ- ,k∈Z,
所以函数的定义域为{x| x≠-4kπ- ,k∈Z}.
{x| x≠-4kπ- ,k∈Z}
(3)函数y= +lg(1-tan x)的定义域为_____________________________.
≥ 0
1-tan x>0
-1≤<1
在(- )上满足上述不等式的x的取值范围是[- ).
又因为y=tan x的周期为π,
所以所求x的定义域为
(1)求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数y=tan x有意义即x≠ +kπ,k∈Z.
技法点拨
求正切函数定义域的方法
(2)求正切型函数y=Atan(ωx+φ)(A≠0,ω>0)的定义域时,要将“ωx+φ”视为一个“整体”.令ωx+φ≠kπ+,k∈Z,解得x.
技法点拨
解形如tan x>a的不等式的步骤
易错提醒:求定义域时,要注意正切函数自身的限制条件.
跟踪训练
1.函数y= 的定义域是( )
A. {x|x = k , k∈Z} B. {x| k
B
>0
< 0
<
<
, k∈Z
2.求函数y=tan2 +tan+1的定义域和值域.
由3x+≠ kπ+,k∈Z,得x≠ + (k∈Z),
所以函数的定义域为{x| x≠ + (k∈Z)}.
设t=tan,
则t∈R,y=t2+t+1= 2+ ≥ ,
所以原函数的值域是[,+∞).
题型二 正切函数奇偶性、周期性和图像的对称性
[例2] (1)函数f(x)=tan 的周期为________.
(2)已知函数y=tan ,则该函数图像的对称中心坐标为________.
(3)判断下列函数的奇偶性:
①y=3xtan 2x-2x4; ②y=cos+tan x.
[例2] (1)函数f(x)=tan 的周期为________.
∵tan =tan ,
即tan =tan ,
∴f(x)=tan 的周期是.
法一:(定义法)
法二:(公式法)
f(x)=tan 的周期T= .
[例2] (2)已知函数y=tan ,则该函数图像的对称中心坐标为_______________.
所以图像的对称中心坐标为(+ ,0),k∈Z.
由x- = (k∈Z)得x= + (k∈Z),
(+ , 0),k∈Z
②y=cos+tan x.
[例2] (3)判断下列函数的奇偶性:
①y=3xtan 2x-2x4;
又f(-x)=3(-x)tan 2(-x)-2(-x)4=3xtan 2x-2x4=f(x),
定义域为{x|x≠ + , k∈Z},
关于原点对称,
所以它是偶函数.
定义域为{x|x≠+ , k∈Z} ,
关于原点对称,
y=cos()+tan x=sin x+tan x,
又f(-x)=sin(-x)+tan(-x)=-sin x-tan x=-f(x),
所以它是奇函数.
(3)观察法(或图像法):观察函数的图像,看自变量间隔多少,函数值重复出现.
函数f(x)=Atan(ωx+φ)周期的求解方法
(1)定义法.
(2)公式法:对于函数f(x)=Atan(ωx+φ)的最小正周期T= .
方法总结
先求函数的定义域,看其定义域是否关于原点对称,
若其不关于原点对称,则该函数为非奇非偶函数;
若其关于原点对称,再看f(-x)与f(x)的关系.
判定与正切函数有关的函数奇偶性的方法
提醒:y=tan x,x≠kπ+ ,k∈Z的对称中心坐标为(,0),k∈Z.
方法总结
跟踪训练
(1) f(x)= ;
(2) f(x)=tan +tan .
3.判断下列函数的奇偶性
(1) f(x)= ;
3.判断下列函数的奇偶性
f(x)的定义域为{x|x≠+ 且x≠+ , k∈Z},
所以函数f(x)既不是偶函数,也不是奇函数.
不关于原点对称,
由
x≠+ , k∈Z
1
得
(2) f(x)=tan +tan .
3.判断下列函数的奇偶性
函数定义域为{x|x≠且x≠+ , k∈Z},
关于原点对称,
又f(-x)=tan +tan
=-tan -tan
=-f(x),
所以函数f(x)是奇函数.
题型三 正切函数单调性的应用
1.正切函数y=tan x在其定义域内是否为增函数?
提示:不是.正切函数的图像被直线x=kπ+(k∈Z)隔开,所以它的单调区间只在(kπ, kπ+)(k∈Z)内,而不能说它在定义域内是增函数.假设x1=,x2= π,x1
2.如果让你比较tan()与tan ()的大小,你应该怎样做?
提示:先根据正切函数的周期性把两角化到同一单调区间内,再由正切函数的单调性进行比较.
[探究问题]
[例3] (1) tan 1,tan 2,tan 3,tan 4从小到大的排列顺序为________________________.
y=tan x在区间(, )上是单调增函数,且tan 1=tan(π+1),
所以tan 2<tan 3<tan 4<tan 1.
又<2<3<4<π+1< ,
tan 2<tan 3<tan 4<tan 1
[例3] (2)求函数y=3tan 的单调区间.
y=3tan =-3tan ,
由-+kπ<2x-<+kπ,k∈Z得,
-+ π<x< + π,k∈Z,
所以y=3tan 的减区间为(-+π,+π),k∈Z.
多维探究
变式1 求函数y=3tan 的单调区间.
由kπ-< x-
变式2 求函数y=lgtan的单调区间.
因为函数y=lg x在(0,+∞)上为增函数.
所以函数y=lgtan x的单调递增区间就是函数y=tan x(tan x>0)的递增区间,
即(kπ, +kπ),k∈Z.
(2)若ω<0,可利用诱导公式先把y=Atan(ωx+φ)转化为y=Atan[-(-ωx-φ)]=-Atan(-ωx-φ),即把x的系数化为正值,再利用“整体代换”的思想,求得x的范围即可.
求函数y=Atan(ωx+φ)(A>0,ω≠0,且A,ω,φ都是常数)的单调区间的方法
(1)若ω>0,由于y=tan x在每一个单调区间上都是增函数,故可用“整体代换”的思想,令kπ-<ωx+φ<kπ+ ,k∈Z,解得x的范围即可.
方法总结
易错提醒:y=Atan(ωx+φ)(A>0,ω>0)只有增区间;y=Atan(ωx+φ)(A<0,ω>0)只有减区间.
运用正切函数单调性比较大小的步骤
(1)运用函数的周期性或诱导公式将角化到同一单调区间内.
(2)运用单调性比较大小关系.
方法总结
随堂检测
1.思考辨析
(1)正切函数的定义域和值域都是R.( )
(2)正切函数图像是中心对称图形,有无数个对称中心.( )
(3)正切函数图像有无数条对称轴,其对称轴是x=kπ±,k∈Z.( )
(4)正切函数是增函数.( )
×
√
×
×
2.若tan x≥1,则( )
A.2kπ-<x<2kπ(k∈Z)
B.x≤(2k+1)π(k∈Z)
C.kπ-<x≤kπ(k∈Z)
D.kπ+ ≤x<kπ+ (k∈Z)
D
3.求函数y=tan(π-x),x∈(-, )的值域为__________.
所以值域为(- ,1).
y=tan(π-x)=-tan x,
在(-, )上为减函数,
(- ,1)
4.求函数y=tan 的定义域、最小正周期、单调区间及其图像的对称中心.
②T= =2π,∴函数的最小正周期为2π.
①由≠kπ+ ,k∈Z,得x≠2kπ+ ,k∈Z,
∴函数的定义域为{x|x≠ 2kπ+ ,k∈Z}.
④由=,k∈Z,得x=kπ+,k∈Z,
∴函数图像的对称中心是(kπ+,0),k∈Z.
③由kπ-< <kπ+,k∈Z,得2kπ-<x<2kπ+,k∈Z,
∴函数的单调递增区间为(2kπ-, 2kπ+), k∈Z.
1.利用单位圆中的正切线作正切函数的图像,作图较为准确,但画图时较繁,我们常用“三点两线”法作正切曲线的简图.
本课小结
2.正切函数与正弦函数、余弦函数的性质比较.
本课小结
通过本节课,你学会了什么?
