人教B版(2019)数学必修第三册 8_2_1两角差的余弦课件(共36张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第三册 8_2_1两角差的余弦课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 00:00:00 | ||
图片预览











文档简介
(共36张PPT)
两角差的余弦公式
高一必修第三册
本节目标
1.熟悉两角差的余弦公式的推导过程.
2.熟记两角差的余弦公式,并能灵活运用.
课前预习
(1)如何用α的三角函数与β的三角函数表示cos(α-β)
(2)两角差的余弦公式是如何推导的?
预习课本,思考并完成以下问题
课前小测
1.sin 14°cos 16°+sin 76°cos 74°=( )
A. B.
C.- D.-
B
∴原式=cos 76°cos 16°+sin 76°sin 16°
=cos(76°-16°)=cos 60°=
∵sin 14°=cos 76°,cos 74°=sin 16°
2.cos(-15°)的值是( )
A. B.
C. D.
D
cos(-15°)=cos15°=cos(45°-30°)
=cos 45°cos 30°+sin 45°sin 30°
= ×+×
=
3.cos 65°cos 20°+sin 65°sin 20°=________.
cos 65°cos 20°+sin 65°sin 20°
=cos(65°-20°)
=cos 45°
=
新知探究
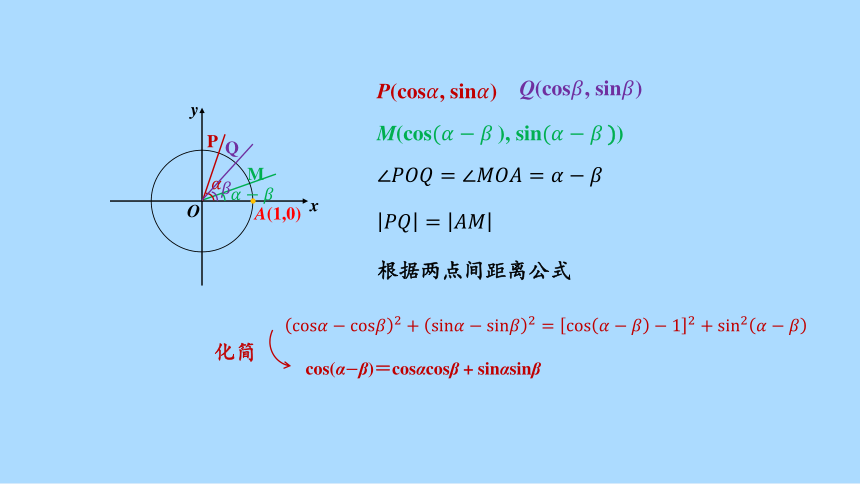
x
y
O
A(1,0)
P
Q
M
P(cos, sin)
Q(cos, sin)
M(cos), sin)
根据两点间距离公式
cos(αβ)=cosαcosβ + sinαsinβ
化简
两角差的余弦公式
cos αcos β+sin αsin β
题型突破
典例深度剖析 重点多维探究
题型一 给角求值问题
[例1] (1) cos 的值为( )
A. B.
C. D.-
D
cos =cos(+ )=-cos =-cos (-)
=-cos cos -sin sin =- × - × =-
(2) 求下列各式的值:
①cos 75°cos 15°-sin 75°sin 195°;
②sin 46°cos 14°+sin 44°cos 76°;
③ cos 15°+ sin 15°.
(2) 求下列各式的值:
①cos 75°cos 15°-sin 75°sin 195°;
cos 75°cos 15°-sin 75°sin 195°
=cos 75°cos 15°-sin 75°sin(180°+15°)
=cos 75°cos 15°+sin 75°sin 15°
=cos(75°-15°)
=cos 60°
=
(2) 求下列各式的值:
②sin 46°cos 14°+sin 44°cos 76°;
sin 46°cos 14°+sin 44°cos 76°
=sin(90°-44°)cos 14°+sin 44°cos(90°-14°)
=cos 44°cos 14°+sin 44°sin 14°
=cos(44°-14°)
=cos 30°
=
(2) 求下列各式的值:
③ cos 15°+ sin 15°
cos 15°+ sin 15°
=cos 60°cos 15°+sin 60°sin 15°
=cos(60°-15°)
=cos 45°
=
(1)把非特殊角转化为特殊角的和或差,正用公式直接求值.
(2)在转化过程中,充分利用诱导公式,构造两角差的余弦公式的结构形式,然后逆用公式求值.
(1)同名函数相乘:即两角余弦乘余弦,正弦乘正弦.
(2)把所得的积相加.
1.解含非特殊角的三角函数式的求值问题的一般思路
2.两角差的余弦公式的结构特点
反思感悟
跟踪训练
1.化简下列各式:
(1) cos(θ+21°)cos(θ-24°)+sin(θ+21°)sin(θ-24°);
(2) -sin 167°·sin 223°+sin 257°·sin 313°.
1.化简下列各式:
(1) cos(θ+21°)cos(θ-24°)+sin(θ+21°)sin(θ-24°);
原式=cos[θ+21°-(θ-24°)]
=cos 45°
=
1.化简下列各式:
(2) -sin 167°·sin 223°+sin 257°·sin 313°.
原式=-sin(180°-13°)sin(180°+43°)+sin(180°+77°)·sin(360°-47°)
=sin 13°sin 43°+sin 77°sin 47°
=sin 13°sin 43°+cos 13°cos 43°
=cos(13°-43°)
=cos(-30°)
=
题型二 给值(式)求值问题
1.若已知α+β和β的三角函数值,如何求cos α的值?
提示:cos α=cos[(α+β)-β]
=cos(α+β)cos β+sin(α+β)sin β.
[探究问题]
题型二 给值(式)求值问题
2.利用α-(α-β)=β可得cos β等于什么?
提示:cos β=cos[α-(α-β)]
=cos αcos(α-β)+sin αsin(α-β).
[探究问题]
[例2] (1)已知sin α-sin β=1- ,cos α-cos β= ,则cos(α-β)=( )
A.- B.- C. D.
因为sin α-sin β=1-,所以sin2α-2sin αsin β+sin2β=(1-)2, ①
因为cos α-cos β=,所以cos2α-2cos αcos β+cos2β=()2, ②
①,②两式相加得1-2cos(α-β)+1=1-+ +
所以-2cos(α-β)=-
所以cos(α-β)= .
D
[例2] (2)已知sin = ,α∈(, ),求cos α的值.
∵α∈(, ) ,∴ +α∈ (,) ,
∴cos =- =-=- .
∵α= - ,
∴ cos α=cos(- )=cos cos +sin sin
=-× + × = .
多维探究
变式1 已知sin= ,且 <α < ,求cos α的值.
<α <
<α+ <
cos= - = -
∴cos α=cos[]
=cos cos +sin sin
=-× + ×
=
变式2 已知sin = ,α∈(, ),求cos (α )的值.
∵ <α< ,∴-< -α< ,
又sin =- <0,
∴-< -α<0,cos = = ,
∴cos (α ) =cos () =cos[ ]
= cos + sin
= × + ×(-)=-
2 由于和、差角与单角是相对的,因此解题过程中可以根据需要灵活地进行拆角或凑角.常见角的变换有:
①α= α-β +β; ② α= +
③2α= α+β + α-β ; ④2β= α+β - α-β .
给值求值问题的解题策略
1 已知某些角的三角函数值,求另外一些角的三角函数值时,要注意观察已知角与所求表达式中角的关系,即拆角与凑角.
解题策略
题型三 给值求角问题
[例3] 已知sin(π-α)=,cos(α-β)=,0<β<α< ,求角β的大小.
因为sin(π-α)= ,所以sin α= .
因为0<α< ,所以cos α= =.
因为cos(α-β)=,且0<β<α< ,所以0<α-β< ,
所以sin(α-β)= = ,
所以cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)= ×+ × =.因为0<β< ,所以β= .
1 界定角的范围,根据条件确定所求角的范围.
2 求所求角的某种三角函数值.为防止增解最好选取在范围内单调的三角函数.
3 结合三角函数值及角的范围求角.
已知三角函数值求角的解题步骤
提醒:在根据三角函数值求角时,易忽视角的范围,而得到错误答案.
归纳总结
跟踪训练
2.已知α,β均为锐角,且cos α=,cos β=,求α-β的值.
∴cos(α-β)=cos αcos β+sin αsin β
= × + × =
∵α,β均为锐角
∴sin α=,sin β=
又sin α故α-β=-.
随堂检测
1.思考辨析
(1)cos(60°-30°)=cos 60°-cos 30°.( )
(2)对于任意实数α,β,cos(α-β)=cos α-cos β都不成立.( )
(3)对任意α,β∈R,cos(α-β)=cos αcos β+sin αsin β都成立.( )
(4)cos 30°cos 120°+sin 30°sin 120°=0.( )
×
×
√
√
当α=-45°,β=45°时成立
2.已知α为锐角,β为第三象限角,且cos α=,sin β=-,则cos(α-β)的值为( )
A.- B.- C. D.
∵α为锐角,cos α=,∴sin α= = ,
∵β为第三象限角,sin β=-,∴cos β=- =-,
∴cos(α-β)=cos αcos β+sin αsin β= ×(-)+ ×(-)=-.
A
3.cos(α-35°)cos(α+25°)+sin(α-35°)sin(α+25°)=_____.
原式=cos[(α-35°)-(α+25°)]
=cos(-60°)=cos 60°
=
4.已知sin α=-,sin β= ,且180°<α<270°,90°<β<180°,求cos(α-β)的值.
因为sin α=-,180°<α<270°,所以cos α=-.
因为sin β=,90°<β<180°,所以cos β=-,
所以cos(α-β)=cos αcos β+sin αsin β
=(-)×(-)+(-)×
=-=
2.“给值求角”问题,实际上也可转化为“给值求值”问题,求一个角的值,可分以下三步进行:
①求角的某一三角函数值;
②确定角所在的范围(找一个单调区间);
③确定角的值.确定用所求角的哪种三角函数值,要根据具体题目而定.
1.给式求值或给值求值问题,即由给出的某些函数关系式或某些角的三角函数值,求另外一些角的三角函数值,关键在于“变式”或“变角”,使“目标角”换成“已知角”.注意公式的正用、逆用、变形用,有时需运用拆角、拼角等技巧.
本课小结
通过本节课,你学会了什么?
两角差的余弦公式
高一必修第三册
本节目标
1.熟悉两角差的余弦公式的推导过程.
2.熟记两角差的余弦公式,并能灵活运用.
课前预习
(1)如何用α的三角函数与β的三角函数表示cos(α-β)
(2)两角差的余弦公式是如何推导的?
预习课本,思考并完成以下问题
课前小测
1.sin 14°cos 16°+sin 76°cos 74°=( )
A. B.
C.- D.-
B
∴原式=cos 76°cos 16°+sin 76°sin 16°
=cos(76°-16°)=cos 60°=
∵sin 14°=cos 76°,cos 74°=sin 16°
2.cos(-15°)的值是( )
A. B.
C. D.
D
cos(-15°)=cos15°=cos(45°-30°)
=cos 45°cos 30°+sin 45°sin 30°
= ×+×
=
3.cos 65°cos 20°+sin 65°sin 20°=________.
cos 65°cos 20°+sin 65°sin 20°
=cos(65°-20°)
=cos 45°
=
新知探究
x
y
O
A(1,0)
P
Q
M
P(cos, sin)
Q(cos, sin)
M(cos), sin)
根据两点间距离公式
cos(αβ)=cosαcosβ + sinαsinβ
化简
两角差的余弦公式
cos αcos β+sin αsin β
题型突破
典例深度剖析 重点多维探究
题型一 给角求值问题
[例1] (1) cos 的值为( )
A. B.
C. D.-
D
cos =cos(+ )=-cos =-cos (-)
=-cos cos -sin sin =- × - × =-
(2) 求下列各式的值:
①cos 75°cos 15°-sin 75°sin 195°;
②sin 46°cos 14°+sin 44°cos 76°;
③ cos 15°+ sin 15°.
(2) 求下列各式的值:
①cos 75°cos 15°-sin 75°sin 195°;
cos 75°cos 15°-sin 75°sin 195°
=cos 75°cos 15°-sin 75°sin(180°+15°)
=cos 75°cos 15°+sin 75°sin 15°
=cos(75°-15°)
=cos 60°
=
(2) 求下列各式的值:
②sin 46°cos 14°+sin 44°cos 76°;
sin 46°cos 14°+sin 44°cos 76°
=sin(90°-44°)cos 14°+sin 44°cos(90°-14°)
=cos 44°cos 14°+sin 44°sin 14°
=cos(44°-14°)
=cos 30°
=
(2) 求下列各式的值:
③ cos 15°+ sin 15°
cos 15°+ sin 15°
=cos 60°cos 15°+sin 60°sin 15°
=cos(60°-15°)
=cos 45°
=
(1)把非特殊角转化为特殊角的和或差,正用公式直接求值.
(2)在转化过程中,充分利用诱导公式,构造两角差的余弦公式的结构形式,然后逆用公式求值.
(1)同名函数相乘:即两角余弦乘余弦,正弦乘正弦.
(2)把所得的积相加.
1.解含非特殊角的三角函数式的求值问题的一般思路
2.两角差的余弦公式的结构特点
反思感悟
跟踪训练
1.化简下列各式:
(1) cos(θ+21°)cos(θ-24°)+sin(θ+21°)sin(θ-24°);
(2) -sin 167°·sin 223°+sin 257°·sin 313°.
1.化简下列各式:
(1) cos(θ+21°)cos(θ-24°)+sin(θ+21°)sin(θ-24°);
原式=cos[θ+21°-(θ-24°)]
=cos 45°
=
1.化简下列各式:
(2) -sin 167°·sin 223°+sin 257°·sin 313°.
原式=-sin(180°-13°)sin(180°+43°)+sin(180°+77°)·sin(360°-47°)
=sin 13°sin 43°+sin 77°sin 47°
=sin 13°sin 43°+cos 13°cos 43°
=cos(13°-43°)
=cos(-30°)
=
题型二 给值(式)求值问题
1.若已知α+β和β的三角函数值,如何求cos α的值?
提示:cos α=cos[(α+β)-β]
=cos(α+β)cos β+sin(α+β)sin β.
[探究问题]
题型二 给值(式)求值问题
2.利用α-(α-β)=β可得cos β等于什么?
提示:cos β=cos[α-(α-β)]
=cos αcos(α-β)+sin αsin(α-β).
[探究问题]
[例2] (1)已知sin α-sin β=1- ,cos α-cos β= ,则cos(α-β)=( )
A.- B.- C. D.
因为sin α-sin β=1-,所以sin2α-2sin αsin β+sin2β=(1-)2, ①
因为cos α-cos β=,所以cos2α-2cos αcos β+cos2β=()2, ②
①,②两式相加得1-2cos(α-β)+1=1-+ +
所以-2cos(α-β)=-
所以cos(α-β)= .
D
[例2] (2)已知sin = ,α∈(, ),求cos α的值.
∵α∈(, ) ,∴ +α∈ (,) ,
∴cos =- =-=- .
∵α= - ,
∴ cos α=cos(- )=cos cos +sin sin
=-× + × = .
多维探究
变式1 已知sin= ,且 <α < ,求cos α的值.
<α <
<α+ <
cos= - = -
∴cos α=cos[]
=cos cos +sin sin
=-× + ×
=
变式2 已知sin = ,α∈(, ),求cos (α )的值.
∵ <α< ,∴-< -α< ,
又sin =- <0,
∴-< -α<0,cos = = ,
∴cos (α ) =cos () =cos[ ]
= cos + sin
= × + ×(-)=-
2 由于和、差角与单角是相对的,因此解题过程中可以根据需要灵活地进行拆角或凑角.常见角的变换有:
①α= α-β +β; ② α= +
③2α= α+β + α-β ; ④2β= α+β - α-β .
给值求值问题的解题策略
1 已知某些角的三角函数值,求另外一些角的三角函数值时,要注意观察已知角与所求表达式中角的关系,即拆角与凑角.
解题策略
题型三 给值求角问题
[例3] 已知sin(π-α)=,cos(α-β)=,0<β<α< ,求角β的大小.
因为sin(π-α)= ,所以sin α= .
因为0<α< ,所以cos α= =.
因为cos(α-β)=,且0<β<α< ,所以0<α-β< ,
所以sin(α-β)= = ,
所以cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)= ×+ × =.因为0<β< ,所以β= .
1 界定角的范围,根据条件确定所求角的范围.
2 求所求角的某种三角函数值.为防止增解最好选取在范围内单调的三角函数.
3 结合三角函数值及角的范围求角.
已知三角函数值求角的解题步骤
提醒:在根据三角函数值求角时,易忽视角的范围,而得到错误答案.
归纳总结
跟踪训练
2.已知α,β均为锐角,且cos α=,cos β=,求α-β的值.
∴cos(α-β)=cos αcos β+sin αsin β
= × + × =
∵α,β均为锐角
∴sin α=,sin β=
又sin α
随堂检测
1.思考辨析
(1)cos(60°-30°)=cos 60°-cos 30°.( )
(2)对于任意实数α,β,cos(α-β)=cos α-cos β都不成立.( )
(3)对任意α,β∈R,cos(α-β)=cos αcos β+sin αsin β都成立.( )
(4)cos 30°cos 120°+sin 30°sin 120°=0.( )
×
×
√
√
当α=-45°,β=45°时成立
2.已知α为锐角,β为第三象限角,且cos α=,sin β=-,则cos(α-β)的值为( )
A.- B.- C. D.
∵α为锐角,cos α=,∴sin α= = ,
∵β为第三象限角,sin β=-,∴cos β=- =-,
∴cos(α-β)=cos αcos β+sin αsin β= ×(-)+ ×(-)=-.
A
3.cos(α-35°)cos(α+25°)+sin(α-35°)sin(α+25°)=_____.
原式=cos[(α-35°)-(α+25°)]
=cos(-60°)=cos 60°
=
4.已知sin α=-,sin β= ,且180°<α<270°,90°<β<180°,求cos(α-β)的值.
因为sin α=-,180°<α<270°,所以cos α=-.
因为sin β=,90°<β<180°,所以cos β=-,
所以cos(α-β)=cos αcos β+sin αsin β
=(-)×(-)+(-)×
=-=
2.“给值求角”问题,实际上也可转化为“给值求值”问题,求一个角的值,可分以下三步进行:
①求角的某一三角函数值;
②确定角所在的范围(找一个单调区间);
③确定角的值.确定用所求角的哪种三角函数值,要根据具体题目而定.
1.给式求值或给值求值问题,即由给出的某些函数关系式或某些角的三角函数值,求另外一些角的三角函数值,关键在于“变式”或“变角”,使“目标角”换成“已知角”.注意公式的正用、逆用、变形用,有时需运用拆角、拼角等技巧.
本课小结
通过本节课,你学会了什么?
