人教B版(2019)数学必修第三册7_1_2弧度制及其与角度制的换算课件(共34张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第三册7_1_2弧度制及其与角度制的换算课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1012.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 00:00:00 | ||
图片预览










文档简介
(共34张PPT)
弧度制及其与角度制的换算
高一
必修三
本节目标
1.理解角度制与弧度制的概念,能对弧度和角度进行正确的转换.
2.体会引入弧度制的必要性,建立角的集合与实数集一一对应关系.
3.掌握并能应用弧度制下的弧长公式和扇形面积公式.
任务一:知识预习
课前预习
预习课本,思考并完成以下问题
(1)1弧度的角是如何定义的?
(2)如何求角α的弧度数?
(3)如何进行弧度与角度的换算?
(4)以弧度为单位的扇形弧长、面积公式是什么?
任务二:简单题型通关
课前预习
D
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
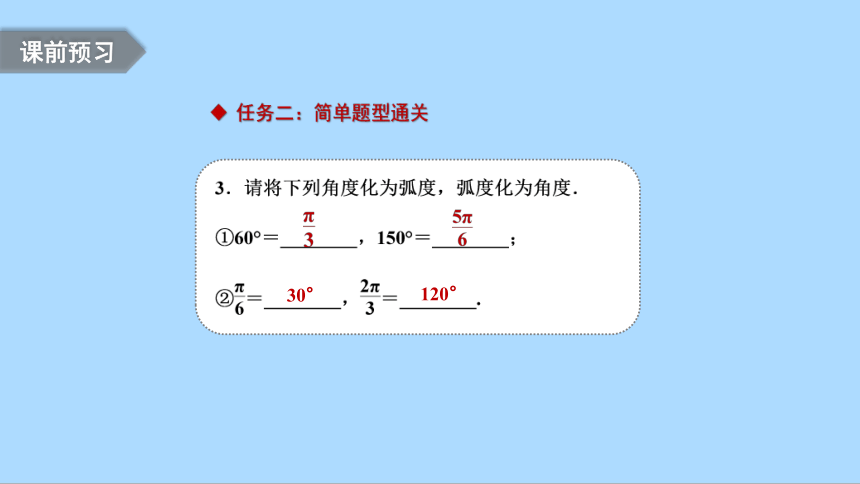
30°
120°
任务二:简单题型通关
课前预习
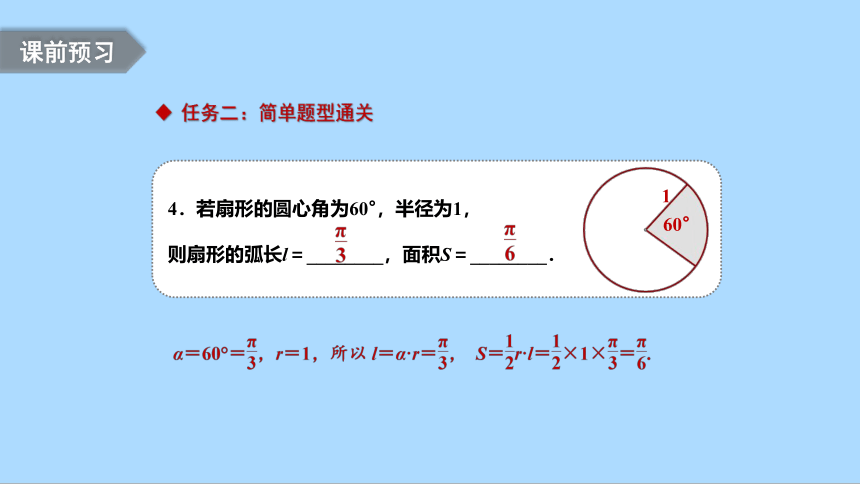
4.若扇形的圆心角为60°,半径为1,
则扇形的弧长l=________,面积S=________.
1
60°
(1)角度制
规定周角的________为1度的角,用度作为单位来度量角的单位制叫做角度制.
(2)弧度制
把长度等于_______的弧所对的_________叫做1弧度的角.以弧度作为单位来度量角的单位制,叫做________,它的单位符号是rad,读作________,通常略去不写.
新知精讲
1.角的单位制
(3)角的弧度数的求法
正角的弧度数是一个________,负角的弧度数是一个________,零角的弧度数是________.如果半径为r的圆的圆心角α所对弧的长为l,那么角α的弧度数的绝对值|α|=________.
新知精讲
1.角的单位制
新知精讲
(1)用弧度为单位表示角的大小时,“弧度”或“rad”可以略去不写,只写这个角对应的弧度数即可,如角α=-3.5 rad可写成α=-3.5.而用角度为单位表示角的大小时,“度”或“°”不可以省略.
(2)不管是以弧度还是以度为单位的角的大小,都是一个与半径的大小无关的定值.
易错提示
新知精讲
2.角度与弧度的换算
新知精讲
3.弧度制下的弧长与扇形面积公式
新知精讲
技巧点拨
题型探究
题型一
角度与弧度的换算
题型探究
题型探究
∴k=-1或k=0.
∴在-360°~360°范围内与β1
终边相同的角是-216°.
归纳总结
角度与弧度的互化技巧
技巧点拨
活学活用
题型探究
题型二
用弧度制表示终边相同的角
题型探究
题型探究
归纳总结
用弧度制表示终边相同的角2kπ+α(k∈Z)时,其中2kπ是π的偶数倍,而不是整数倍,还要注意角度制与弧度制不能混用.
易错提示
活学活用
活学活用
题型探究
题型三
扇形的弧长公式及面积公式
题点一:利用公式求弧长和面积
题型探究
题型三
扇形的弧长公式及面积公式
题点二:利用公式求半径和弧度数
2.扇形OAB的面积是4 cm2,它的周长是8 cm,求扇形的半径和圆心角.
题型探究
题型三
扇形的弧长公式及面积公式
题点三:利用公式求扇形面积的最值
3.已知扇形AOB的周长为10 cm,求该扇形的面积的最大值及取得最大值时圆心角的大小及弧长.
归纳总结
解题攻略
达标检测
1.下列说法中,正确的是( )
A.1弧度是1度的圆心角所对的弧
B.1弧度是长度为半径的弧
C.1弧度是1度的弧与1度的角之和
D.1弧度是长度等于半径长的弧所对的圆心角,弧度是角的一种度量单位
D
达标检测
C
达标检测
D
达标检测
达标检测
本课小结
1. 什么是角度制,什么是弧度制?怎么进行角度与弧度的互化?
2. 扇形的弧长及面积的计算公式.
弧度制及其与角度制的换算
高一
必修三
本节目标
1.理解角度制与弧度制的概念,能对弧度和角度进行正确的转换.
2.体会引入弧度制的必要性,建立角的集合与实数集一一对应关系.
3.掌握并能应用弧度制下的弧长公式和扇形面积公式.
任务一:知识预习
课前预习
预习课本,思考并完成以下问题
(1)1弧度的角是如何定义的?
(2)如何求角α的弧度数?
(3)如何进行弧度与角度的换算?
(4)以弧度为单位的扇形弧长、面积公式是什么?
任务二:简单题型通关
课前预习
D
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
30°
120°
任务二:简单题型通关
课前预习
4.若扇形的圆心角为60°,半径为1,
则扇形的弧长l=________,面积S=________.
1
60°
(1)角度制
规定周角的________为1度的角,用度作为单位来度量角的单位制叫做角度制.
(2)弧度制
把长度等于_______的弧所对的_________叫做1弧度的角.以弧度作为单位来度量角的单位制,叫做________,它的单位符号是rad,读作________,通常略去不写.
新知精讲
1.角的单位制
(3)角的弧度数的求法
正角的弧度数是一个________,负角的弧度数是一个________,零角的弧度数是________.如果半径为r的圆的圆心角α所对弧的长为l,那么角α的弧度数的绝对值|α|=________.
新知精讲
1.角的单位制
新知精讲
(1)用弧度为单位表示角的大小时,“弧度”或“rad”可以略去不写,只写这个角对应的弧度数即可,如角α=-3.5 rad可写成α=-3.5.而用角度为单位表示角的大小时,“度”或“°”不可以省略.
(2)不管是以弧度还是以度为单位的角的大小,都是一个与半径的大小无关的定值.
易错提示
新知精讲
2.角度与弧度的换算
新知精讲
3.弧度制下的弧长与扇形面积公式
新知精讲
技巧点拨
题型探究
题型一
角度与弧度的换算
题型探究
题型探究
∴k=-1或k=0.
∴在-360°~360°范围内与β1
终边相同的角是-216°.
归纳总结
角度与弧度的互化技巧
技巧点拨
活学活用
题型探究
题型二
用弧度制表示终边相同的角
题型探究
题型探究
归纳总结
用弧度制表示终边相同的角2kπ+α(k∈Z)时,其中2kπ是π的偶数倍,而不是整数倍,还要注意角度制与弧度制不能混用.
易错提示
活学活用
活学活用
题型探究
题型三
扇形的弧长公式及面积公式
题点一:利用公式求弧长和面积
题型探究
题型三
扇形的弧长公式及面积公式
题点二:利用公式求半径和弧度数
2.扇形OAB的面积是4 cm2,它的周长是8 cm,求扇形的半径和圆心角.
题型探究
题型三
扇形的弧长公式及面积公式
题点三:利用公式求扇形面积的最值
3.已知扇形AOB的周长为10 cm,求该扇形的面积的最大值及取得最大值时圆心角的大小及弧长.
归纳总结
解题攻略
达标检测
1.下列说法中,正确的是( )
A.1弧度是1度的圆心角所对的弧
B.1弧度是长度为半径的弧
C.1弧度是1度的弧与1度的角之和
D.1弧度是长度等于半径长的弧所对的圆心角,弧度是角的一种度量单位
D
达标检测
C
达标检测
D
达标检测
达标检测
本课小结
1. 什么是角度制,什么是弧度制?怎么进行角度与弧度的互化?
2. 扇形的弧长及面积的计算公式.
