15.3.2 分式方程的实际应用(1)课件(共32张PPT)
文档属性
| 名称 | 15.3.2 分式方程的实际应用(1)课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
15.3.2 分式方程的实际应用(1)
人教版八年级上册
解分式方程的一般步骤
知识回顾
解分式方程的一般步骤
一去
二解
三验
四写
去分母,方程两边同乘最简公分母,把分式方程转化为整式方程.
解这个整式方程.
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
写出原分式方程的解.
1.解分式方程: .
知识巩固
1.解分式方程: .
解:方程两边同时乘以(x+1)(x-1),得2(x+1)=4,
解得x=1.
检验:当x=1时,(x+1)(x-1)=0,
所以x=1不是原分式方程的解,
则原分式方程无解.
工程类应用题
知识回顾
①工作效率=
工作量
工作时间
工程类应用题常用公式
③工作时间=
工作量
工作效率
②工作量=
工作效率×工作时间
1.会列分式方程解决实际问题.
2.能根据题意找出正确的等量关系,列出分式方程并求解,会根据实际意义验证结果是否合理.
教学目标
1.会列分式方程解决实际问题.
2.能根据题意找出正确的等量关系,列出分式方程并求解,会根据实际意义验证结果是否合理.
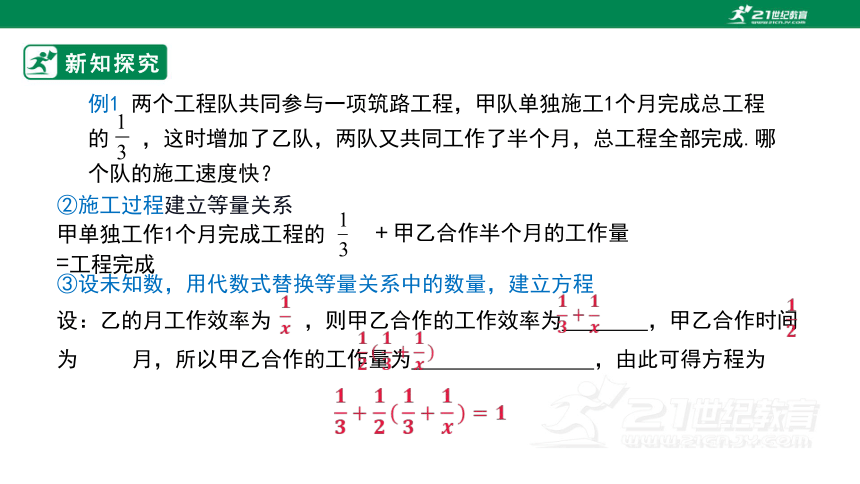
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
新知导入
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
分析(方法1,从施工过程解题):
①读题审题
已知:施工过程,甲先单独工作1个后,甲乙再合作半个月,完成工程。甲工作效率 ,甲乙合作的时间半个月。
未知:求解哪个队的施工速度快? 求乙队工作效率,方可比较甲乙施工速度。
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
利用分式方程解答工程问题
知识点 1
③设未知数,用代数式替换等量关系中的数量,建立方程
设:乙的月工作效率为 ,则甲乙合作的工作效率为 ,甲乙合作时间为 月,所以甲乙合作的工作量为 ,由此可得方程为
新知探究
②施工过程建立等量关系
甲单独工作1个月完成工程的 + =工程完成
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
甲乙合作半个月的工作量
根据题意可,得: .
新知探究
解:设乙队单独施工1个月能完成总工程的
去括号,得:
方程两边同时乘以6x,得2x+x+3=6x.解得x=1.
检验:当x=1时,6x≠0.
所以原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队的施工速度快.
新知探究
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
分析(方法2,从各队施工时间解题):
①读题审题,与方法1相同
②工作时间建立等量关系
甲一共工作了 个月的工作量 + =工程完成
乙一共工作半个月的工作量
③设未知数:设:乙月工作效率为
建立方程:
新知探究
根据题意可,得: .
解:设乙队单独施工1个月能完成总工程的
整理,得:
方程两边同时乘以2x,得x+1=2x.解得x=1.
检验:当x=1时,2x≠0.
所以原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队的施工速度快.
新知小结
从施工过程解题与从工作时间解题对比
使用等量关系
得到的方程
①施工过程建立等量关系
甲单独工作1个月完成工程的 + =工程完成
甲乙合作半个月的工作量
②工作时间建立等量关系
甲一共工作了 个月的工作量 + =工程完成
乙一共工作半个月的工作量
①
②
对比可以发现,施工过程解题中等量关系容易确定,但所列方程解法上有些复杂,工作时间解题中等量关系确定稍复杂,所以在今后的工程类问题中,酌情选用。
新知小结
列分式方程解决实际问题(工程类)的一般步骤
①读题审题,明确已知和未知
②确定等量关系,可从施工过程或工作时间两个角度建立等量关系
③设未知数,可选择设直接未知数或间接未知数,用代数式替换等量关系中的数量,建立方程
④解方程后记得检验,既要检验所得的解是否为所列分式方程的解,又要检验所得的解是否符合实际问题的要求;
⑤答,注意单位和语言完整
新知练习
1.某校改造维修田径运动场所,项目承包单位派遣了一号施工队进场施工,计划用30天完成整个工程,当一号施工队施工10天后,由于实际需要,要求整个工程比原计划提前8天完成,于是承包单位再派遣二号施工队与一号施工队共同施工,结果按实际需要如期完成整个工程。
(1)如果二号施工队单独施工,完成整个工程需要多少天
(2)如果一号、二号施工队同时进场共同施工,完成整个工程需要多少天
分析(方法1,从施工过程解题):
①读题、审题
已知:一号施工队的工作效率为 ,
施工过程为一号施工队先工作 天,然后二号施工队加入,余下项目由两队共同完成,比计划提前8天,完成项目实际用了 天;
未知: 。
二号施工队的工作效率
22
10
新知练习
②施工过程建立等量关系
1.某校改造维修田径运动场所,项目承包单位派遣了一号施工队进场施工,计划用30天完成整个工程,当一号施工队施工10天后,由于实际需要,要求整个工程比原计划提前8天完成,于是承包单位再派遣二号施工队与一号施工队共同施工,结果按实际需要如期完成整个工程。
(1)如果二号施工队单独施工,完成整个工程需要多少天
(2)如果一号、二号施工队同时进场共同施工,完成整个工程需要多少天
一号施工队工作10天的工作量+两队合作 天的工作量=总工作量.
12
③设未知数,用代数式替换等量关系中的数量,建立方程
设二号施工队单独施工,完成整个工程需要x天,即二号施工队的工作效率为 .
新知练习
根据题意可,得: .
解:设二号施工队的工作效率为
整理,得:
方程两边同时乘以15x,得11x+15×12=15x.解得x=45.
检验:当x=45时,15x≠0.
所以原分式方程的解为x=45.
答:若二号施工队单独施工完成全部任务,需要45天。
新知练习
1.某校改造维修田径运动场所,项目承包单位派遣了一号施工队进场施工,计划用30天完成整个工程,当一号施工队施工10天后,由于实际需要,要求整个工程比原计划提前8天完成,于是承包单位再派遣二号施工队与一号施工队共同施工,结果按实际需要如期完成整个工程。
(1)如果二号施工队单独施工,完成整个工程需要多少天
(2)如果一号、二号施工队同时进场共同施工,完成整个工程需要多少天
分析(方法2,从各队施工时间解题):
①读题、审题
已知:一号施工队的工作效率为 ,
各队施工时间:一号施工队从项目开始到完成一共施工 天,二号施工队加入后一共施工了 天;
未知: 。
二号施工队的工作效率
22
12
新知练习
②各队施工时间建立等量关系
1.某校改造维修田径运动场所,项目承包单位派遣了一号施工队进场施工,计划用30天完成整个工程,当一号施工队施工10天后,由于实际需要,要求整个工程比原计划提前8天完成,于是承包单位再派遣二号施工队与一号施工队共同施工,结果按实际需要如期完成整个工程。
(1)如果二号施工队单独施工,完成整个工程需要多少天
(2)如果一号、二号施工队同时进场共同施工,完成整个工程需要多少天
一号施工队22天的工作量+二号施工队12天的工作量=总工作量.
③设未知数,用代数式替换等量关系中的数量,建立方程
设二号施工队单独施工完成整个工程需要x天,即二号施工队的工作效率为 .
新知练习
根据题意可,得: .
解:设二号施工队的工作效率为
整理,得:
方程两边同时乘以15x,得11x+15×12=15x.解得x=45.
检验:当x=45时,15x≠0.
所以原分式方程的解为x=45.
答:若二号施工队单独施工完成全部任务,需要45天。
新知练习
1.某校改造维修田径运动场所,项目承包单位派遣了一号施工队进场施工,计划用30天完成整个工程,当一号施工队施工10天后,由于实际需要,要求整个工程比原计划提前8天完成,于是承包单位再派遣二号施工队与一号施工队共同施工,结果按实际需要如期完成整个工程。
(1)如果二号施工队单独施工,完成整个工程需要多少天
(2)如果一号、二号施工队同时进场共同施工,完成整个工程需要多少天
解:(2)根据题意得:
答:若由一、二号施工队同时进场施工,完成整个工程需要18天
新知练习
2. 某市区一条主要街道的改造工程有甲、乙两个工程队投标,经测算,若由两个工程队共同工作,则恰好12天能够完成任务;若两个工程队共同工作9天后,剩下的任务由甲工程队单独完成,则还需5天.现要从这两个工程队中选出一个工程队单独完成,从缩短工期的角度考虑,你认为应该选择哪个工程队?
分析:根据题中等量关系“甲、乙两个工程队共同工作9天的工作量+甲工程队单独工作5天的工作量=总工作量(记为1)”列方程,再比较甲、乙两个工程队单独完成任务所用的时间,然后做出决策.
新知练习
解:设甲工程队单独完成工程需要x天.
方程两边同时乘以x ,得 ,解得 x=20.
根据题意,得 .
经检验:x=20是原分式方程的解.
因为 ,所以乙工程队单独完成工程需要30天.
因为20<30,所以选择甲队.
答:从缩短工期的角度考虑,应该选择甲工程队.
新知探究
例2 甲、乙两地相距19千米,某人从甲地出发前往乙地,先步行7千米,然后改骑自行车,共用2小时到达乙地.已知这个人骑自行车的速度是步行速度的4倍.求这个人步行时间和骑自行车的速度.
利用分式方程解答行程问题
知识点 2
分析:由“步行和骑自行车共用2小时到达乙地”可知,等量关系为“ ”,为了简化方程,可设 为x,列出方程,求出步行和骑车速度,然后求出步行时间.
步行时间+骑自行车时间=总时间2小时
步行速度
新知探究
例2 甲、乙两地相距19千米,某人从甲地出发前往乙地,先步行7千米,然后改骑自行车,共用2小时到达乙地.已知这个人骑自行车的速度是步行速度的4倍.求这个人步行时间和骑自行车的速度.
解:设步行速度为 x km/h,那么骑车速度是 4x km/h,
解得 x=5
经检验 x=5是原方程的解。
∴4x=20,
∴步行时间为 小时。
答:这个人步行时间为 小时,骑自行车的速度为20km/h。
新知探究
3. 甲、乙两城市相距120千米,甲城市急需物资,乙城市紧急支援一货车物资,已知货车行驶速度是原来速度的1.5倍,从乙城市到甲城市的时间缩短了半小时,求货车提速后的速度.
解:设货车原来的速度为 x km/h,则提速后的速度是1.5x km/h。
解得 x=80
经检验,x=80是原方程的解,且符合题意。
则1.5x=1.5×80=120.
答:货车提速后的速度为120 km/h。
课堂总结
列分式方程解决实际问题
一审
能根据实际问题找出等量关系并列出正确的分式方程
二设
三列
步骤
四解
五验
六答
课堂练习
1.施工队要铺设1000米的管道,因在中考期间需停工2天,每天要比原计划多施工30米才能按时完成任务.设原计划每天施工x米,所列方程正确的是( )
A.
B.
C.
D.
A
天
天
- =2
课堂练习
2.(2020·柳州中考)甲、乙二人做某种机械零件,已知每小时甲比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,设乙每小时做x个零件,以下所列方程正确的是( )
A.
B.
C.
D.
C
=
课堂练习
3. 王鹏家住成都,今年暑假,他们全家计划到贵州旅游,第一站到遵义参观遵义会议遗址.王鹏在做旅游攻略时发现成都火车东站距离遵义火车站530km,乘坐高铁列车从成都火车东站到遵义火车站比乘坐特快列车少用3小时,高铁列车的平均行驶速度是特快列车的2.8倍.请你帮王鹏计算一下从成都火车东站到遵义火车站乘坐高铁列车所需时间.
解:设特快列车的平均行驶速度是x km/h,则高铁列车的平均行驶速度是2.8x km/h。
解得 x=
经检验,x= 是原方程的解,且符合题意。
则 小时 .
答:从成都火车东站到遵义火车站乘坐高铁列车所需时间为 小时。
课堂练习
4.为积极创建全国文明城市,甲、乙两工程队承包了我市某街道路面改造工程.若由甲、乙两工程队合做20天可以完成;若甲工程队先单独施工40天,再由乙工程队单独施工10天也可以完成.求甲、乙两工程队单独完成此项工程各需要多少天?
解得 x=60
经检验,x= 60 是原方程的解,且符合题意。
则乙工程队单独完成需要的天数为 天 .
答:甲乙工程队单独完成此项工程分别需要60天、30天。
解:设甲工程队单独完成需要x天,则甲工程队的工作效率为 ,
乙工程队的工作效率为 .
课堂练习
5.为稳步推进5G网络建设,深化共建共享,现有甲、乙两个工程队参与5G基站建设工程,甲队单独施工20天可完成5G基站建设工程的 ,这时增加了乙队,两队又共同工作了15天后,总工程全部完成,求乙队单独施工需要多少天才能完成这项工程?
解得 x=30
经检验,x= 30 是原方程的解,且符合题意。
则乙工程队单独完成需要的天数为 30 天 .
答:乙工程队单独完成此项工程需要30天。
解:设乙工程队单独完成需要x天,则甲工程队的工作效率为 .
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
15.3.2 分式方程的实际应用(1)
人教版八年级上册
解分式方程的一般步骤
知识回顾
解分式方程的一般步骤
一去
二解
三验
四写
去分母,方程两边同乘最简公分母,把分式方程转化为整式方程.
解这个整式方程.
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
写出原分式方程的解.
1.解分式方程: .
知识巩固
1.解分式方程: .
解:方程两边同时乘以(x+1)(x-1),得2(x+1)=4,
解得x=1.
检验:当x=1时,(x+1)(x-1)=0,
所以x=1不是原分式方程的解,
则原分式方程无解.
工程类应用题
知识回顾
①工作效率=
工作量
工作时间
工程类应用题常用公式
③工作时间=
工作量
工作效率
②工作量=
工作效率×工作时间
1.会列分式方程解决实际问题.
2.能根据题意找出正确的等量关系,列出分式方程并求解,会根据实际意义验证结果是否合理.
教学目标
1.会列分式方程解决实际问题.
2.能根据题意找出正确的等量关系,列出分式方程并求解,会根据实际意义验证结果是否合理.
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
新知导入
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
分析(方法1,从施工过程解题):
①读题审题
已知:施工过程,甲先单独工作1个后,甲乙再合作半个月,完成工程。甲工作效率 ,甲乙合作的时间半个月。
未知:求解哪个队的施工速度快? 求乙队工作效率,方可比较甲乙施工速度。
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
利用分式方程解答工程问题
知识点 1
③设未知数,用代数式替换等量关系中的数量,建立方程
设:乙的月工作效率为 ,则甲乙合作的工作效率为 ,甲乙合作时间为 月,所以甲乙合作的工作量为 ,由此可得方程为
新知探究
②施工过程建立等量关系
甲单独工作1个月完成工程的 + =工程完成
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
甲乙合作半个月的工作量
根据题意可,得: .
新知探究
解:设乙队单独施工1个月能完成总工程的
去括号,得:
方程两边同时乘以6x,得2x+x+3=6x.解得x=1.
检验:当x=1时,6x≠0.
所以原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队的施工速度快.
新知探究
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
分析(方法2,从各队施工时间解题):
①读题审题,与方法1相同
②工作时间建立等量关系
甲一共工作了 个月的工作量 + =工程完成
乙一共工作半个月的工作量
③设未知数:设:乙月工作效率为
建立方程:
新知探究
根据题意可,得: .
解:设乙队单独施工1个月能完成总工程的
整理,得:
方程两边同时乘以2x,得x+1=2x.解得x=1.
检验:当x=1时,2x≠0.
所以原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队的施工速度快.
新知小结
从施工过程解题与从工作时间解题对比
使用等量关系
得到的方程
①施工过程建立等量关系
甲单独工作1个月完成工程的 + =工程完成
甲乙合作半个月的工作量
②工作时间建立等量关系
甲一共工作了 个月的工作量 + =工程完成
乙一共工作半个月的工作量
①
②
对比可以发现,施工过程解题中等量关系容易确定,但所列方程解法上有些复杂,工作时间解题中等量关系确定稍复杂,所以在今后的工程类问题中,酌情选用。
新知小结
列分式方程解决实际问题(工程类)的一般步骤
①读题审题,明确已知和未知
②确定等量关系,可从施工过程或工作时间两个角度建立等量关系
③设未知数,可选择设直接未知数或间接未知数,用代数式替换等量关系中的数量,建立方程
④解方程后记得检验,既要检验所得的解是否为所列分式方程的解,又要检验所得的解是否符合实际问题的要求;
⑤答,注意单位和语言完整
新知练习
1.某校改造维修田径运动场所,项目承包单位派遣了一号施工队进场施工,计划用30天完成整个工程,当一号施工队施工10天后,由于实际需要,要求整个工程比原计划提前8天完成,于是承包单位再派遣二号施工队与一号施工队共同施工,结果按实际需要如期完成整个工程。
(1)如果二号施工队单独施工,完成整个工程需要多少天
(2)如果一号、二号施工队同时进场共同施工,完成整个工程需要多少天
分析(方法1,从施工过程解题):
①读题、审题
已知:一号施工队的工作效率为 ,
施工过程为一号施工队先工作 天,然后二号施工队加入,余下项目由两队共同完成,比计划提前8天,完成项目实际用了 天;
未知: 。
二号施工队的工作效率
22
10
新知练习
②施工过程建立等量关系
1.某校改造维修田径运动场所,项目承包单位派遣了一号施工队进场施工,计划用30天完成整个工程,当一号施工队施工10天后,由于实际需要,要求整个工程比原计划提前8天完成,于是承包单位再派遣二号施工队与一号施工队共同施工,结果按实际需要如期完成整个工程。
(1)如果二号施工队单独施工,完成整个工程需要多少天
(2)如果一号、二号施工队同时进场共同施工,完成整个工程需要多少天
一号施工队工作10天的工作量+两队合作 天的工作量=总工作量.
12
③设未知数,用代数式替换等量关系中的数量,建立方程
设二号施工队单独施工,完成整个工程需要x天,即二号施工队的工作效率为 .
新知练习
根据题意可,得: .
解:设二号施工队的工作效率为
整理,得:
方程两边同时乘以15x,得11x+15×12=15x.解得x=45.
检验:当x=45时,15x≠0.
所以原分式方程的解为x=45.
答:若二号施工队单独施工完成全部任务,需要45天。
新知练习
1.某校改造维修田径运动场所,项目承包单位派遣了一号施工队进场施工,计划用30天完成整个工程,当一号施工队施工10天后,由于实际需要,要求整个工程比原计划提前8天完成,于是承包单位再派遣二号施工队与一号施工队共同施工,结果按实际需要如期完成整个工程。
(1)如果二号施工队单独施工,完成整个工程需要多少天
(2)如果一号、二号施工队同时进场共同施工,完成整个工程需要多少天
分析(方法2,从各队施工时间解题):
①读题、审题
已知:一号施工队的工作效率为 ,
各队施工时间:一号施工队从项目开始到完成一共施工 天,二号施工队加入后一共施工了 天;
未知: 。
二号施工队的工作效率
22
12
新知练习
②各队施工时间建立等量关系
1.某校改造维修田径运动场所,项目承包单位派遣了一号施工队进场施工,计划用30天完成整个工程,当一号施工队施工10天后,由于实际需要,要求整个工程比原计划提前8天完成,于是承包单位再派遣二号施工队与一号施工队共同施工,结果按实际需要如期完成整个工程。
(1)如果二号施工队单独施工,完成整个工程需要多少天
(2)如果一号、二号施工队同时进场共同施工,完成整个工程需要多少天
一号施工队22天的工作量+二号施工队12天的工作量=总工作量.
③设未知数,用代数式替换等量关系中的数量,建立方程
设二号施工队单独施工完成整个工程需要x天,即二号施工队的工作效率为 .
新知练习
根据题意可,得: .
解:设二号施工队的工作效率为
整理,得:
方程两边同时乘以15x,得11x+15×12=15x.解得x=45.
检验:当x=45时,15x≠0.
所以原分式方程的解为x=45.
答:若二号施工队单独施工完成全部任务,需要45天。
新知练习
1.某校改造维修田径运动场所,项目承包单位派遣了一号施工队进场施工,计划用30天完成整个工程,当一号施工队施工10天后,由于实际需要,要求整个工程比原计划提前8天完成,于是承包单位再派遣二号施工队与一号施工队共同施工,结果按实际需要如期完成整个工程。
(1)如果二号施工队单独施工,完成整个工程需要多少天
(2)如果一号、二号施工队同时进场共同施工,完成整个工程需要多少天
解:(2)根据题意得:
答:若由一、二号施工队同时进场施工,完成整个工程需要18天
新知练习
2. 某市区一条主要街道的改造工程有甲、乙两个工程队投标,经测算,若由两个工程队共同工作,则恰好12天能够完成任务;若两个工程队共同工作9天后,剩下的任务由甲工程队单独完成,则还需5天.现要从这两个工程队中选出一个工程队单独完成,从缩短工期的角度考虑,你认为应该选择哪个工程队?
分析:根据题中等量关系“甲、乙两个工程队共同工作9天的工作量+甲工程队单独工作5天的工作量=总工作量(记为1)”列方程,再比较甲、乙两个工程队单独完成任务所用的时间,然后做出决策.
新知练习
解:设甲工程队单独完成工程需要x天.
方程两边同时乘以x ,得 ,解得 x=20.
根据题意,得 .
经检验:x=20是原分式方程的解.
因为 ,所以乙工程队单独完成工程需要30天.
因为20<30,所以选择甲队.
答:从缩短工期的角度考虑,应该选择甲工程队.
新知探究
例2 甲、乙两地相距19千米,某人从甲地出发前往乙地,先步行7千米,然后改骑自行车,共用2小时到达乙地.已知这个人骑自行车的速度是步行速度的4倍.求这个人步行时间和骑自行车的速度.
利用分式方程解答行程问题
知识点 2
分析:由“步行和骑自行车共用2小时到达乙地”可知,等量关系为“ ”,为了简化方程,可设 为x,列出方程,求出步行和骑车速度,然后求出步行时间.
步行时间+骑自行车时间=总时间2小时
步行速度
新知探究
例2 甲、乙两地相距19千米,某人从甲地出发前往乙地,先步行7千米,然后改骑自行车,共用2小时到达乙地.已知这个人骑自行车的速度是步行速度的4倍.求这个人步行时间和骑自行车的速度.
解:设步行速度为 x km/h,那么骑车速度是 4x km/h,
解得 x=5
经检验 x=5是原方程的解。
∴4x=20,
∴步行时间为 小时。
答:这个人步行时间为 小时,骑自行车的速度为20km/h。
新知探究
3. 甲、乙两城市相距120千米,甲城市急需物资,乙城市紧急支援一货车物资,已知货车行驶速度是原来速度的1.5倍,从乙城市到甲城市的时间缩短了半小时,求货车提速后的速度.
解:设货车原来的速度为 x km/h,则提速后的速度是1.5x km/h。
解得 x=80
经检验,x=80是原方程的解,且符合题意。
则1.5x=1.5×80=120.
答:货车提速后的速度为120 km/h。
课堂总结
列分式方程解决实际问题
一审
能根据实际问题找出等量关系并列出正确的分式方程
二设
三列
步骤
四解
五验
六答
课堂练习
1.施工队要铺设1000米的管道,因在中考期间需停工2天,每天要比原计划多施工30米才能按时完成任务.设原计划每天施工x米,所列方程正确的是( )
A.
B.
C.
D.
A
天
天
- =2
课堂练习
2.(2020·柳州中考)甲、乙二人做某种机械零件,已知每小时甲比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,设乙每小时做x个零件,以下所列方程正确的是( )
A.
B.
C.
D.
C
=
课堂练习
3. 王鹏家住成都,今年暑假,他们全家计划到贵州旅游,第一站到遵义参观遵义会议遗址.王鹏在做旅游攻略时发现成都火车东站距离遵义火车站530km,乘坐高铁列车从成都火车东站到遵义火车站比乘坐特快列车少用3小时,高铁列车的平均行驶速度是特快列车的2.8倍.请你帮王鹏计算一下从成都火车东站到遵义火车站乘坐高铁列车所需时间.
解:设特快列车的平均行驶速度是x km/h,则高铁列车的平均行驶速度是2.8x km/h。
解得 x=
经检验,x= 是原方程的解,且符合题意。
则 小时 .
答:从成都火车东站到遵义火车站乘坐高铁列车所需时间为 小时。
课堂练习
4.为积极创建全国文明城市,甲、乙两工程队承包了我市某街道路面改造工程.若由甲、乙两工程队合做20天可以完成;若甲工程队先单独施工40天,再由乙工程队单独施工10天也可以完成.求甲、乙两工程队单独完成此项工程各需要多少天?
解得 x=60
经检验,x= 60 是原方程的解,且符合题意。
则乙工程队单独完成需要的天数为 天 .
答:甲乙工程队单独完成此项工程分别需要60天、30天。
解:设甲工程队单独完成需要x天,则甲工程队的工作效率为 ,
乙工程队的工作效率为 .
课堂练习
5.为稳步推进5G网络建设,深化共建共享,现有甲、乙两个工程队参与5G基站建设工程,甲队单独施工20天可完成5G基站建设工程的 ,这时增加了乙队,两队又共同工作了15天后,总工程全部完成,求乙队单独施工需要多少天才能完成这项工程?
解得 x=30
经检验,x= 30 是原方程的解,且符合题意。
则乙工程队单独完成需要的天数为 30 天 .
答:乙工程队单独完成此项工程需要30天。
解:设乙工程队单独完成需要x天,则甲工程队的工作效率为 .
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
