26.2.2 实际问题与反比例函数(第2课时)课件(共29张PPT)
文档属性
| 名称 | 26.2.2 实际问题与反比例函数(第2课时)课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
实际问题与反比例函数(第2课时)
1.通过对“杠杆原理”等实际问题与反比例函数关系的探究,使学生体会数学建模思想和学以致用的数学理念,并能从函数的观点来解决一些实际问题. (重点)
2.掌握反比例函数在其他学科中的运用,体验学科的整合思想. (重点、难点)
给我一个支点,我可以把地球撬动!
---阿基米德
公元前3世纪,古希腊科学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡. 后来人们把它归纳为“杠杆原理”. 通俗地说,杠杆原理为:
阻力×阻力臂=动力×动力臂
例1.小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5m.
(1)动力F与动力臂l有怎样的函数关系?当动力臂为1.5m时,撬动石头至少需要多大的力?
(2)若想使动力F不超过题(1)中所用力的一半,则动力臂l至少要加长多少?
解:根据“杠杆原理”,得Fl=1200×0.5,
所以F关于l的函数解析式为
当l=1.5m时,
因此撬动石头至少需要400N的力.
例1.小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5m.
(2)若想使动力F不超过题(1)中所用力的一半,则动力臂l至少要加长多少?
解:对于函数 ,F随l的增大而减小.因此,只要求出F=200N时对应的l的值,就能确定动力臂l至少应加长的量.
当F=400×0.5=200N时,
3-1.5=1.5m
对于函数 ,当l>0时,l越大,F越小. 因此,若想用力不超过400N 的一半,则动力臂至少要加长1.5m.
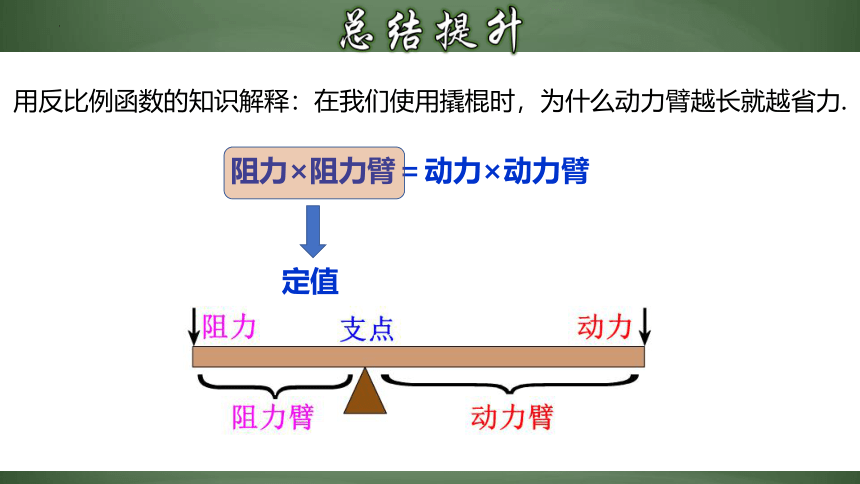
用反比例函数的知识解释:在我们使用撬棍时,为什么动力臂越长就越省力.
阻力×阻力臂=动力×动力臂
定值
某同学设计了如下杠杆平衡实验:如图,取一根长65cm的质地,均匀木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧,距离中点20cm处挂一个重9N的物体,在中点的右侧,用一个弹簧测力计向下拉,使木杆保持平衡(动力×动力臂=阻力×阻力臂),改变弹簧测力计与中点O的距离L(单位:cm),观察弹簧测力计的示数F(单位:N). 通过实验,得到下表数据:
第1组 第2组 第3组 第4组 第5组
L/cm 20 24 25 28 30
F/N 9 7.5 10 6
(1)解:∵阻力×阻力臂是个定值,
∴随着L的增大,F会减小,
∴第3组是明显错误的;
(2)解:设F L=k,则k=9×20=180,
∴F L=180;
(3)解:∵,
∴当F≤10(N)时,,L≥18(cm),
∵木杆长65cm,O是木杆的中点,
∴L≤32.5(cm),
∴18cm≤L≤32.5cm.
例2.某校科技小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地. 当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强p(Pa)也随之变化变化. 如果人和木板对湿地地面的压力合计为 600N,那么
(1)用含S的代数式表示p,p是S的反比例函数吗?为什么?
解:由 得
p是S的反比例函数,因为给定一个S的值,对应的就有唯一的一个p值和它对应,根据函数定义,则p是S的反比例函数.
(2)当木板面积为0.2m2时,压强是多少?
解:当S=0.2m2时,
故当木板面积为0.2m2时,压强是3000Pa.
(3) 如果要求压强不超过6000Pa,木板面积至少要多大?
解:当p=6000时,由 得
对于函数 ,当S>0时,S越大,p越小. 因此,若要求压强不超过6000Pa,则木板面积至少要0.1m2.
某种气球内充满了一定质量的气体,当温度不变时,气球内气体的压强与气球体积之间成反比例关系,其图象如图所示.
(1)当时,求P的值;
(2)当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于多少?
解:(1)设这个函数解析式为:,
代入点A的坐标得,,
∴,
∴这个函数的解析式为;
将代入得:
∴(Pa),
∴P的值是帕;
某种气球内充满了一定质量的气体,当温度不变时,气球内气体的压强与气球体积之间成反比例关系,其图象如图所示.
(1)当时,求P的值;
(2)当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于多少?
(2)∵气球内气体的压强大于时,气球将爆炸,
∴为了安全起见,
,
,
∴为了安全起见,气球的体积不少于 .
电学知识告诉我们,用电器的功率P(单位:W)、两端的电压U(单位:V)及用电器的电阻R(单位:Ω)有如下关系:PR=U2.
这个关系也可写为P=_____,或R=_____.
例3.一个用电器的电阻是可调节的,其范围为110--220Ω.已知电压为220V,这个用电器的电路图如图所示.
(1)功率P与电阻R有怎样的函数关系?
(2)这个用电器功率的范围是多少?
解:(1)根据电学知识,当U=220时,得
例3.一个用电器的电阻是可调节的,其范围为110--220Ω.已知电压为220V,这个用电器的电路图如图所示.
(2)这个用电器功率的范围是多少?
(2)根据反比例函数的性质可知,电阻越大,功率越小.
把电阻的最小值R=110代入①式,得到功率
的最大值 (W)
把电阻的最大值R=220代入①式,得到功率
的最小值 (W)
因此用电器功率的范围为220--440W.
结合例3,想一想为什么收音机的音量、某些台灯的亮度以及电风扇的转速可以调节.
收音机的音量、台灯的亮度以及电风扇的转速由用电器的功率决定.
一辆汽车前灯电路上的电压U(V)保持不变,选用灯泡的电阻为R(),通过的电流强度为I(A),由欧姆定律可知,.当电阻为时,测得通过的电流强度为0.4A.
(1)求I关于R的函数表达式.
(2)为了保证电流强度不超过0.6A,求选用灯泡电阻的取值范围.
(1)解:∵电阻为时,电流强度为0.4A,
∴,即(V).
∴.
一辆汽车前灯电路上的电压U(V)保持不变,选用灯泡的电阻为R(),通过的电流强度为I(A),由欧姆定律可知,.当电阻为时,测得通过的电流强度为0.4A.
(1)求I关于R的函数表达式.
(2)为了保证电流强度不超过0.6A,求选用灯泡电阻的取值范围.
(2)解:∵,,
∴,
∵,
∴解得(),
故选用灯泡电阻的取值范围为.
1.古希腊学者阿基米德发现了著名的“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂.几位同学玩撬石头游戏,已知阻力(石头重量)和阻力臂分别为1600N和0.5m,小明最多能使出500N的力量,若要撬动这块大石头,他该选择撬棍的动力臂( )
A.至多为 B.至少为 C.至多为D.至少为
B
2.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点在其图象上,则当力达到10N时,物体在力的方向上移动的距离是( )
A.2.4m B.1.2m C.1m D.0.5m
B
3.在显示汽车油箱内油量的装置模拟示意图中,电压一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积与电路中总电阻是反比例关系,电流与也是反比例关系,则与的函数关系是( )
A.反比例函数 B.正比例函数
C.二次函数 D.以上答案都不对
B
4.如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现,如图2是该台灯的电流与电阻成反比例函数的图象,该图象经过点.根据图象可知,下列说法正确的是( )
A.当时,
B.I与R的函数关系式是
C.当时,
D.当时,I的取值范围是
D
5.某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这个函数的表达式及写出变量V的取值范围;
(2)当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于128kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
(1)解:设该函数表达式为 .
将点A代入表达式中可得,
∴,
∴该函数表达式为.
5.某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这个函数的表达式及写出变量V的取值范围;
(2)当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于128kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
(2)解:将 代入表达式中可得,
∴气体体积为1m3时,气压是96kPa.
(3)由题意可知,
解得 ,
∴为了安全考虑,气体的体积应不小于0.75 m3.
6.在某一电路中,保持电压U(V)不变,电流I(A)是电阻R( )的反比例函数,如图是某电路电流、电阻的关系图,其图象经过点A(4,9).
(1)求I与R的函数表达式;
(2)当电阻为3 时,求电流大小;
(3)如图该电路的限制电流不能超过10A,那么该电路的可变电阻控制在什么范围?
(1)解:由题意可得,
∵图象过点A(4,9),
∴(V).
∴I与R的函数表达式为.
6.在某一电路中,保持电压U(V)不变,电流I(A)是电阻R( )的反比例函数,如图是某电路电流、电阻的关系图,其图象经过点A(4,9).
(1)求I与R的函数表达式;
(2)当电阻为3 时,求电流大小;
(3)如图该电路的限制电流不能超过10A,那么该电路的可变电阻控制在什么范围?
(2)解:当Ω时,(A),
∴电流大小为12A.
6.在某一电路中,保持电压U(V)不变,电流I(A)是电阻R( )的反比例函数,如图是某电路电流、电阻的关系图,其图象经过点A(4,9).
(1)求I与R的函数表达式;
(2)当电阻为3 时,求电流大小;
(3)如图该电路的限制电流不能超过10A,那么该电路的可变电阻控制在什么范围?
(3)解:由函数图像可知,电路中可变电阻越大,电流越小,当A时,
Ω
所以,该电路的限制电流不能超过10A时,可变电阻控制范围为Ω.
实际问题与反比例函数(第2课时)
1.通过对“杠杆原理”等实际问题与反比例函数关系的探究,使学生体会数学建模思想和学以致用的数学理念,并能从函数的观点来解决一些实际问题. (重点)
2.掌握反比例函数在其他学科中的运用,体验学科的整合思想. (重点、难点)
给我一个支点,我可以把地球撬动!
---阿基米德
公元前3世纪,古希腊科学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡. 后来人们把它归纳为“杠杆原理”. 通俗地说,杠杆原理为:
阻力×阻力臂=动力×动力臂
例1.小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5m.
(1)动力F与动力臂l有怎样的函数关系?当动力臂为1.5m时,撬动石头至少需要多大的力?
(2)若想使动力F不超过题(1)中所用力的一半,则动力臂l至少要加长多少?
解:根据“杠杆原理”,得Fl=1200×0.5,
所以F关于l的函数解析式为
当l=1.5m时,
因此撬动石头至少需要400N的力.
例1.小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5m.
(2)若想使动力F不超过题(1)中所用力的一半,则动力臂l至少要加长多少?
解:对于函数 ,F随l的增大而减小.因此,只要求出F=200N时对应的l的值,就能确定动力臂l至少应加长的量.
当F=400×0.5=200N时,
3-1.5=1.5m
对于函数 ,当l>0时,l越大,F越小. 因此,若想用力不超过400N 的一半,则动力臂至少要加长1.5m.
用反比例函数的知识解释:在我们使用撬棍时,为什么动力臂越长就越省力.
阻力×阻力臂=动力×动力臂
定值
某同学设计了如下杠杆平衡实验:如图,取一根长65cm的质地,均匀木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧,距离中点20cm处挂一个重9N的物体,在中点的右侧,用一个弹簧测力计向下拉,使木杆保持平衡(动力×动力臂=阻力×阻力臂),改变弹簧测力计与中点O的距离L(单位:cm),观察弹簧测力计的示数F(单位:N). 通过实验,得到下表数据:
第1组 第2组 第3组 第4组 第5组
L/cm 20 24 25 28 30
F/N 9 7.5 10 6
(1)解:∵阻力×阻力臂是个定值,
∴随着L的增大,F会减小,
∴第3组是明显错误的;
(2)解:设F L=k,则k=9×20=180,
∴F L=180;
(3)解:∵,
∴当F≤10(N)时,,L≥18(cm),
∵木杆长65cm,O是木杆的中点,
∴L≤32.5(cm),
∴18cm≤L≤32.5cm.
例2.某校科技小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地. 当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强p(Pa)也随之变化变化. 如果人和木板对湿地地面的压力合计为 600N,那么
(1)用含S的代数式表示p,p是S的反比例函数吗?为什么?
解:由 得
p是S的反比例函数,因为给定一个S的值,对应的就有唯一的一个p值和它对应,根据函数定义,则p是S的反比例函数.
(2)当木板面积为0.2m2时,压强是多少?
解:当S=0.2m2时,
故当木板面积为0.2m2时,压强是3000Pa.
(3) 如果要求压强不超过6000Pa,木板面积至少要多大?
解:当p=6000时,由 得
对于函数 ,当S>0时,S越大,p越小. 因此,若要求压强不超过6000Pa,则木板面积至少要0.1m2.
某种气球内充满了一定质量的气体,当温度不变时,气球内气体的压强与气球体积之间成反比例关系,其图象如图所示.
(1)当时,求P的值;
(2)当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于多少?
解:(1)设这个函数解析式为:,
代入点A的坐标得,,
∴,
∴这个函数的解析式为;
将代入得:
∴(Pa),
∴P的值是帕;
某种气球内充满了一定质量的气体,当温度不变时,气球内气体的压强与气球体积之间成反比例关系,其图象如图所示.
(1)当时,求P的值;
(2)当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于多少?
(2)∵气球内气体的压强大于时,气球将爆炸,
∴为了安全起见,
,
,
∴为了安全起见,气球的体积不少于 .
电学知识告诉我们,用电器的功率P(单位:W)、两端的电压U(单位:V)及用电器的电阻R(单位:Ω)有如下关系:PR=U2.
这个关系也可写为P=_____,或R=_____.
例3.一个用电器的电阻是可调节的,其范围为110--220Ω.已知电压为220V,这个用电器的电路图如图所示.
(1)功率P与电阻R有怎样的函数关系?
(2)这个用电器功率的范围是多少?
解:(1)根据电学知识,当U=220时,得
例3.一个用电器的电阻是可调节的,其范围为110--220Ω.已知电压为220V,这个用电器的电路图如图所示.
(2)这个用电器功率的范围是多少?
(2)根据反比例函数的性质可知,电阻越大,功率越小.
把电阻的最小值R=110代入①式,得到功率
的最大值 (W)
把电阻的最大值R=220代入①式,得到功率
的最小值 (W)
因此用电器功率的范围为220--440W.
结合例3,想一想为什么收音机的音量、某些台灯的亮度以及电风扇的转速可以调节.
收音机的音量、台灯的亮度以及电风扇的转速由用电器的功率决定.
一辆汽车前灯电路上的电压U(V)保持不变,选用灯泡的电阻为R(),通过的电流强度为I(A),由欧姆定律可知,.当电阻为时,测得通过的电流强度为0.4A.
(1)求I关于R的函数表达式.
(2)为了保证电流强度不超过0.6A,求选用灯泡电阻的取值范围.
(1)解:∵电阻为时,电流强度为0.4A,
∴,即(V).
∴.
一辆汽车前灯电路上的电压U(V)保持不变,选用灯泡的电阻为R(),通过的电流强度为I(A),由欧姆定律可知,.当电阻为时,测得通过的电流强度为0.4A.
(1)求I关于R的函数表达式.
(2)为了保证电流强度不超过0.6A,求选用灯泡电阻的取值范围.
(2)解:∵,,
∴,
∵,
∴解得(),
故选用灯泡电阻的取值范围为.
1.古希腊学者阿基米德发现了著名的“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂.几位同学玩撬石头游戏,已知阻力(石头重量)和阻力臂分别为1600N和0.5m,小明最多能使出500N的力量,若要撬动这块大石头,他该选择撬棍的动力臂( )
A.至多为 B.至少为 C.至多为D.至少为
B
2.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点在其图象上,则当力达到10N时,物体在力的方向上移动的距离是( )
A.2.4m B.1.2m C.1m D.0.5m
B
3.在显示汽车油箱内油量的装置模拟示意图中,电压一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积与电路中总电阻是反比例关系,电流与也是反比例关系,则与的函数关系是( )
A.反比例函数 B.正比例函数
C.二次函数 D.以上答案都不对
B
4.如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现,如图2是该台灯的电流与电阻成反比例函数的图象,该图象经过点.根据图象可知,下列说法正确的是( )
A.当时,
B.I与R的函数关系式是
C.当时,
D.当时,I的取值范围是
D
5.某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这个函数的表达式及写出变量V的取值范围;
(2)当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于128kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
(1)解:设该函数表达式为 .
将点A代入表达式中可得,
∴,
∴该函数表达式为.
5.某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这个函数的表达式及写出变量V的取值范围;
(2)当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于128kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
(2)解:将 代入表达式中可得,
∴气体体积为1m3时,气压是96kPa.
(3)由题意可知,
解得 ,
∴为了安全考虑,气体的体积应不小于0.75 m3.
6.在某一电路中,保持电压U(V)不变,电流I(A)是电阻R( )的反比例函数,如图是某电路电流、电阻的关系图,其图象经过点A(4,9).
(1)求I与R的函数表达式;
(2)当电阻为3 时,求电流大小;
(3)如图该电路的限制电流不能超过10A,那么该电路的可变电阻控制在什么范围?
(1)解:由题意可得,
∵图象过点A(4,9),
∴(V).
∴I与R的函数表达式为.
6.在某一电路中,保持电压U(V)不变,电流I(A)是电阻R( )的反比例函数,如图是某电路电流、电阻的关系图,其图象经过点A(4,9).
(1)求I与R的函数表达式;
(2)当电阻为3 时,求电流大小;
(3)如图该电路的限制电流不能超过10A,那么该电路的可变电阻控制在什么范围?
(2)解:当Ω时,(A),
∴电流大小为12A.
6.在某一电路中,保持电压U(V)不变,电流I(A)是电阻R( )的反比例函数,如图是某电路电流、电阻的关系图,其图象经过点A(4,9).
(1)求I与R的函数表达式;
(2)当电阻为3 时,求电流大小;
(3)如图该电路的限制电流不能超过10A,那么该电路的可变电阻控制在什么范围?
(3)解:由函数图像可知,电路中可变电阻越大,电流越小,当A时,
Ω
所以,该电路的限制电流不能超过10A时,可变电阻控制范围为Ω.
