2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册4.2.1等差数列的概念第二课时 课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册4.2.1等差数列的概念第二课时 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 608.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 12:52:58 | ||
图片预览






文档简介
(共22张PPT)
4.2.1 等差数列的概念
第二课时等差数列的性质
2、等差数列的通项公式
1、等差数列的定义
3、等差数列的中项
复习
通项公式的证明及推广
10与18
解析:
思考
结论:
等差数列与一次函数的关系
等差数列的判定
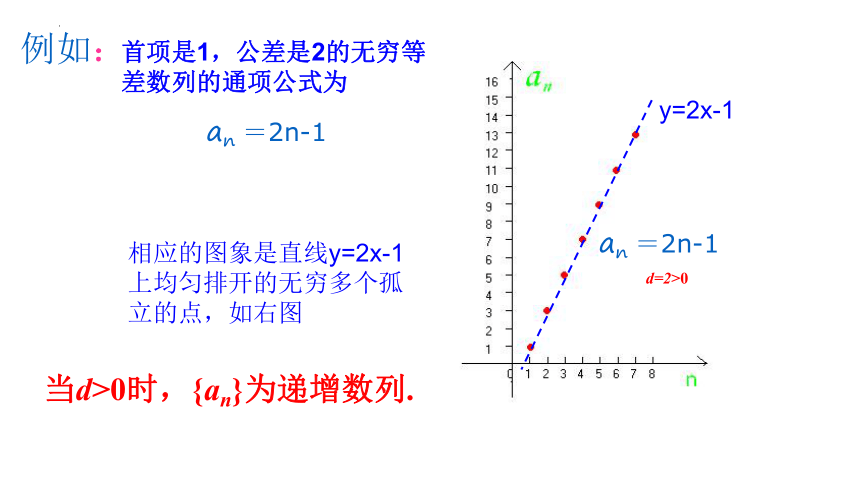
首项是1,公差是2的无穷等差数列的通项公式为
an =2n-1
相应的图象是直线y=2x-1上均匀排开的无穷多个孤立的点,如右图
例如:
当d>0时,{an}为递增数列.
an =2n-1
y=2x-1
d=2>0
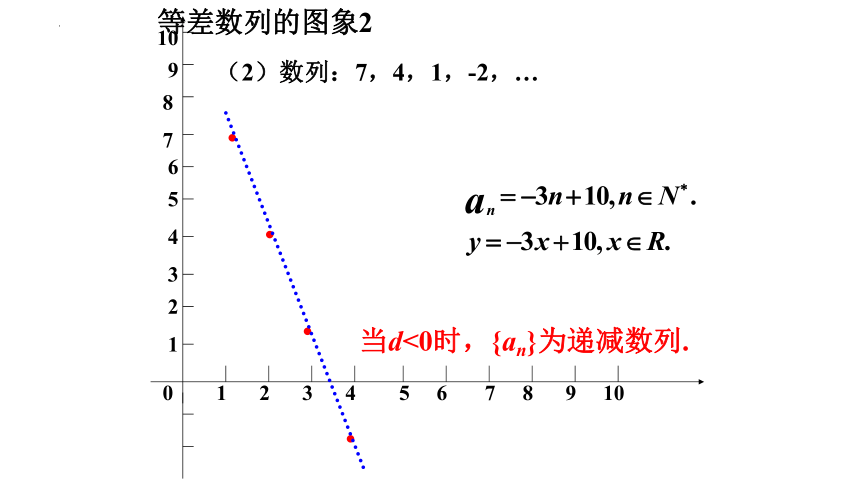
等差数列的图象2
(2)数列:7,4,1,-2,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
当d<0时,{an}为递减数列.
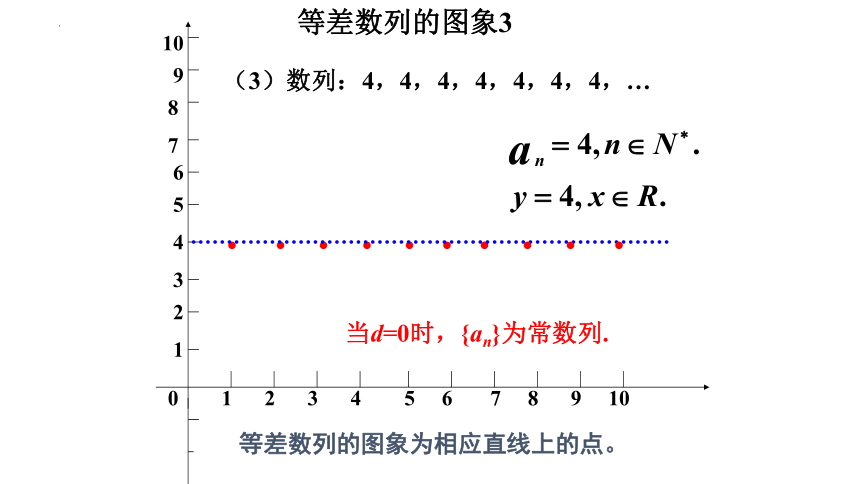
等差数列的图象3
(3)数列:4,4,4,4,4,4,4,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
●
●
●
等差数列的图象为相应直线上的点。
当d=0时,{an}为常数列.
性质 :设 若 则
等差数列的性质
数列{an}是等差数列,m、n、p、q∈N+,且m+n=p+q,则am+an=ap+aq。
判断:
可推广到三项,四项等
注意:等式两边作和的项数必须一样多
∴a8=26-a2=26-4=22.
若m+n=p+q,则am+an=ap+aq
等差数列{an}中,a7=6,
则a1+a13=___
a6+a8=____
12
12
a3+a11= a4+a10=
特别地:当p=q时,am+an=2ap
12
12
例.在等差数列{an}中,a5+a13=40,求a8+a9+a10的值
解析:
设此数列的首项为a1,公差为d,则
a5+a13=(a1+4d)+(a1+12d)
=2a1+16d=40,
即a1+8d=20.
a8+a9+a10=a1+7d)+(a1+8d)+(a1+9d)
=3a1+24d
=3(a1+8d)
=60.
可以应用等差数列的性质:
若m+n=p+q(m,n,p,q∈N*),
则am+an=ap+aq,
当p=q时,am+an=2ap
法二:
有a8+a10=a5+a1=2a9=40,
故a8+a9+a10=( a8+a10 ) +a9
= 3 a9 =60
法一
=a9
例8
(1)已知等差数列{an}中, a3 +a15=30,求a9, a7+a11
解:
(1)∵a9是a3和a15的等差中项
∴
(2)已知等差数列{an}中,
a3 +a4+a5 +a6 +a7=150,
求a2+a8的值
∵7+11=3+15
(2)∵3+7=4+6=5+5
∴ a3 +a4+a5 +a6 +a7=5 a5=150
即a5=30
故a2+a8 =2 a5=60
∴ a7+a11 =a3 +a15=30
∴ a3+a7 =a4 +a6=2 a5
请在此添加文字说明,编辑文字。请在此添加文字说明,编辑文字。请在此添加文字说明,编辑文字。
请在此添加文字说明,编辑文字。请在此添加文字说明,编辑文字。请在此添加文字说明,编辑文字。
添加标题
1.若数列{an}是等差数列,p为常数,那么数列
{an +c}、{pan} 是否为等差数列,请说明理由.
思考
2.若数列{an}、{bn}都是等差数列,那么数列
{an+bn},{an-bn}是否为等差数列,请说明理由.
例 已知三个数成等差数列,它们的和是12,积是48,求这三个数.
解:设三个数为a-d,a,a+d,则
解之得
故所求三数依次为2,4,6或6,4,2
等差数列中的设项方法与技巧
特别地:当p=q时,am+an=2ap
例 已知单调递增的等差数列{an}的前3项之和为21,前3项之积为231,求数列{an}的通项公式.
练习:已知数列{an}是等差数列,若a1-a5+a9-a13+a17=117,求a3+a15的值.
解:∵a1+a17=a5+a13
∴a1-a5+a9-a13+a17 =117.
(a1+a17)-(a5+a13)+a9=117.
a9=117.
∴a3+a15=2a9
=2×117=234.
=2a9
【例】 在等差数列{an}中,
(1)已知a2+a3+a23+a24=48, (2)已知a2+a3+a4+a5=34,
求a13; a2·a5=52,求公差d.
解:(1)根据已知条件
a2+a3+a23+a24=48,
a2+a24 +a3+a23 =48
得2a13 + 2a13 =48.
∴a13=12.
(2)由a2+a3+a4+a5=34,
=-3
4.2.1 等差数列的概念
第二课时等差数列的性质
2、等差数列的通项公式
1、等差数列的定义
3、等差数列的中项
复习
通项公式的证明及推广
10与18
解析:
思考
结论:
等差数列与一次函数的关系
等差数列的判定
首项是1,公差是2的无穷等差数列的通项公式为
an =2n-1
相应的图象是直线y=2x-1上均匀排开的无穷多个孤立的点,如右图
例如:
当d>0时,{an}为递增数列.
an =2n-1
y=2x-1
d=2>0
等差数列的图象2
(2)数列:7,4,1,-2,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
当d<0时,{an}为递减数列.
等差数列的图象3
(3)数列:4,4,4,4,4,4,4,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
●
●
●
等差数列的图象为相应直线上的点。
当d=0时,{an}为常数列.
性质 :设 若 则
等差数列的性质
数列{an}是等差数列,m、n、p、q∈N+,且m+n=p+q,则am+an=ap+aq。
判断:
可推广到三项,四项等
注意:等式两边作和的项数必须一样多
∴a8=26-a2=26-4=22.
若m+n=p+q,则am+an=ap+aq
等差数列{an}中,a7=6,
则a1+a13=___
a6+a8=____
12
12
a3+a11= a4+a10=
特别地:当p=q时,am+an=2ap
12
12
例.在等差数列{an}中,a5+a13=40,求a8+a9+a10的值
解析:
设此数列的首项为a1,公差为d,则
a5+a13=(a1+4d)+(a1+12d)
=2a1+16d=40,
即a1+8d=20.
a8+a9+a10=a1+7d)+(a1+8d)+(a1+9d)
=3a1+24d
=3(a1+8d)
=60.
可以应用等差数列的性质:
若m+n=p+q(m,n,p,q∈N*),
则am+an=ap+aq,
当p=q时,am+an=2ap
法二:
有a8+a10=a5+a1=2a9=40,
故a8+a9+a10=( a8+a10 ) +a9
= 3 a9 =60
法一
=a9
例8
(1)已知等差数列{an}中, a3 +a15=30,求a9, a7+a11
解:
(1)∵a9是a3和a15的等差中项
∴
(2)已知等差数列{an}中,
a3 +a4+a5 +a6 +a7=150,
求a2+a8的值
∵7+11=3+15
(2)∵3+7=4+6=5+5
∴ a3 +a4+a5 +a6 +a7=5 a5=150
即a5=30
故a2+a8 =2 a5=60
∴ a7+a11 =a3 +a15=30
∴ a3+a7 =a4 +a6=2 a5
请在此添加文字说明,编辑文字。请在此添加文字说明,编辑文字。请在此添加文字说明,编辑文字。
请在此添加文字说明,编辑文字。请在此添加文字说明,编辑文字。请在此添加文字说明,编辑文字。
添加标题
1.若数列{an}是等差数列,p为常数,那么数列
{an +c}、{pan} 是否为等差数列,请说明理由.
思考
2.若数列{an}、{bn}都是等差数列,那么数列
{an+bn},{an-bn}是否为等差数列,请说明理由.
例 已知三个数成等差数列,它们的和是12,积是48,求这三个数.
解:设三个数为a-d,a,a+d,则
解之得
故所求三数依次为2,4,6或6,4,2
等差数列中的设项方法与技巧
特别地:当p=q时,am+an=2ap
例 已知单调递增的等差数列{an}的前3项之和为21,前3项之积为231,求数列{an}的通项公式.
练习:已知数列{an}是等差数列,若a1-a5+a9-a13+a17=117,求a3+a15的值.
解:∵a1+a17=a5+a13
∴a1-a5+a9-a13+a17 =117.
(a1+a17)-(a5+a13)+a9=117.
a9=117.
∴a3+a15=2a9
=2×117=234.
=2a9
【例】 在等差数列{an}中,
(1)已知a2+a3+a23+a24=48, (2)已知a2+a3+a4+a5=34,
求a13; a2·a5=52,求公差d.
解:(1)根据已知条件
a2+a3+a23+a24=48,
a2+a24 +a3+a23 =48
得2a13 + 2a13 =48.
∴a13=12.
(2)由a2+a3+a4+a5=34,
=-3
