2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和公式(第一课时)课件(共25张PPT)
文档属性
| 名称 | 2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和公式(第一课时)课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
4.2.2 等差数列的前n项和公式
第1课时
2、等差数列的通项公式
1、等差数列的定义
3、等差数列的中项
复习
通项公式的证明及推广
100与180
特别地:当m+n=2p时,am+an=2ap
创设情境
据说,200多年前,高斯的算术老师提出了下面的问题:
1+2+3+…+100=?
你准备怎么算呢?
探究新知
高斯(gauss,1777-1855),德国数学家,近代数学的奠基者之一. 他在天文学、大地测量学、磁学、光学等领域都做出过杰出贡献.
问题1:为什么1+100=2+99=…=50+51呢?
这是巧合吗?试从数列角度给出解释.
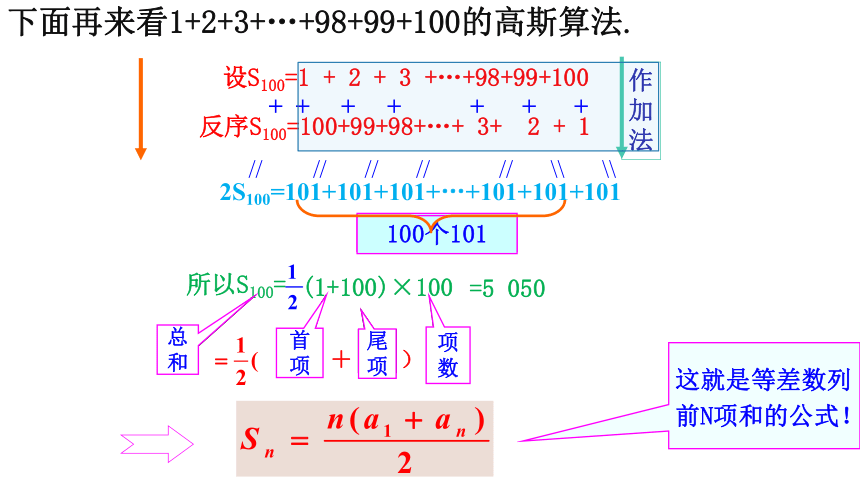
下面再来看1+2+3+…+98+99+100的高斯算法.
设s100=1 + 2 + 3 +…+98+99+100
反序s100=100+99+98+…+ 3+ 2 + 1
作
加
法
多少个101
100个101
2s100=101+101+101+…+101+101+101
// // // // // \\ \\
+ + + + + + +
所以s100=
(1+100)×100
?
?
首项
尾项
?
总
和
?
项数
这就是等差数列前n项和的公式!
=5 050
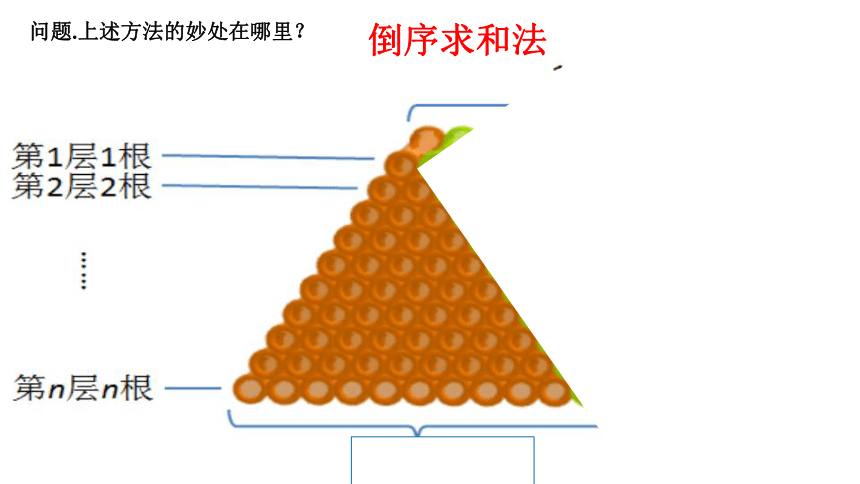
问题.上述方法的妙处在哪里?
倒序求和法
+ 得:2sn=(a1+an)+(a2+an-1)+(a3+an-2)+…+(an+a1).
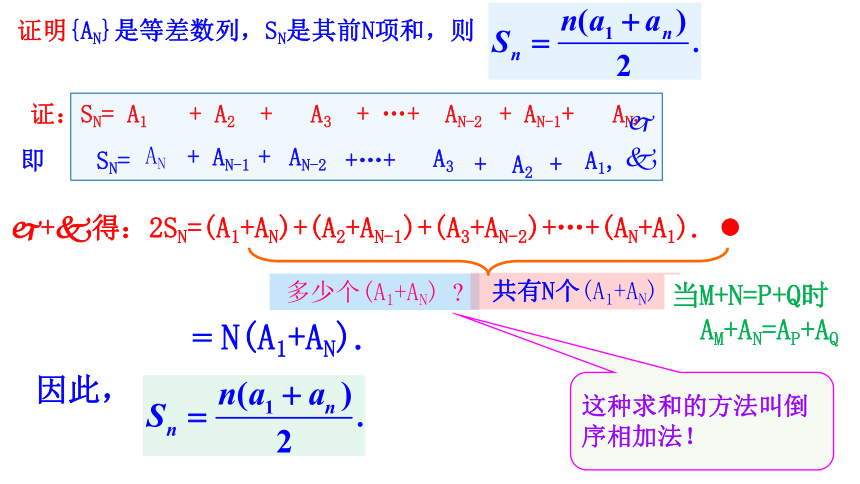
证明{an}是等差数列,sn是其前n项和,则
证:sn= a1 + a2 + a3 + …+ an-2 + an-1+ an,
即 sn=
a1,
an
+ a2 +
+ an-1 +
a3
an-2
+…+
多少个(a1+an)
共有n个(a1+an)
= n(a1+an).
这种求和的方法叫倒序相加法!
因此,
当m+n=p+q时
am+an=ap+aq
【即时练习】
由以上例题可以得出:在求等差数列的前n项的和时,当知道首项和公差,或者首项和末项,均可以得出.
已知等差数列an中a2+a5+a12+a15=36.求前16项的和
由等差数列的性质可得:
a1+a16=a2+a15=a5+a12=36/2=18
=(16/2 )×18
=144
分析:可以由等差数列性质,直接代入前n项和公式.
例 1:
解:
16
a2+a15
答:前16项的和为144
探究 等差数列的前n项和公式的其他形式
例
练习
等差数列 -10,-6,-2,2,…前多少项的和是54?
解:
n1=9,n2=-3
等差数列-10,-6,-2,2,…前9项的和是54.
例3:
设题中的等差数列为{an},前n项和是 sn,
则a1= -10,d= -6-(-10) = 4,设 sn=54,
根据等差数列前 n项和公式,得
又因为n要为正整数
(舍去)
c
解得a1=-1,d=1,
所以a100=-1+99×1=98.
∴a100=a10+90d=98.
探究 等差数列的前n项和公式的其他形式
( 注意 a 还可以是 0)
一个关于 的,没有 的“ ”
n
常数项
二次函数
b
a
a
b
已知一个等差数列的前10项的和是310,前20项的和是1220,求sn.
解:
s10=310,
s20=1 220
例 4:
=n2-8-(n-1)2+8
=2n-1.
这个公式非常重要,适合于所有的数列求和,并不是只适合于等差数列,需完全掌握。
小结
知三求二
4.2.2 等差数列的前n项和公式
第1课时
2、等差数列的通项公式
1、等差数列的定义
3、等差数列的中项
复习
通项公式的证明及推广
100与180
特别地:当m+n=2p时,am+an=2ap
创设情境
据说,200多年前,高斯的算术老师提出了下面的问题:
1+2+3+…+100=?
你准备怎么算呢?
探究新知
高斯(gauss,1777-1855),德国数学家,近代数学的奠基者之一. 他在天文学、大地测量学、磁学、光学等领域都做出过杰出贡献.
问题1:为什么1+100=2+99=…=50+51呢?
这是巧合吗?试从数列角度给出解释.
下面再来看1+2+3+…+98+99+100的高斯算法.
设s100=1 + 2 + 3 +…+98+99+100
反序s100=100+99+98+…+ 3+ 2 + 1
作
加
法
多少个101
100个101
2s100=101+101+101+…+101+101+101
// // // // // \\ \\
+ + + + + + +
所以s100=
(1+100)×100
?
?
首项
尾项
?
总
和
?
项数
这就是等差数列前n项和的公式!
=5 050
问题.上述方法的妙处在哪里?
倒序求和法
+ 得:2sn=(a1+an)+(a2+an-1)+(a3+an-2)+…+(an+a1).
证明{an}是等差数列,sn是其前n项和,则
证:sn= a1 + a2 + a3 + …+ an-2 + an-1+ an,
即 sn=
a1,
an
+ a2 +
+ an-1 +
a3
an-2
+…+
多少个(a1+an)
共有n个(a1+an)
= n(a1+an).
这种求和的方法叫倒序相加法!
因此,
当m+n=p+q时
am+an=ap+aq
【即时练习】
由以上例题可以得出:在求等差数列的前n项的和时,当知道首项和公差,或者首项和末项,均可以得出.
已知等差数列an中a2+a5+a12+a15=36.求前16项的和
由等差数列的性质可得:
a1+a16=a2+a15=a5+a12=36/2=18
=(16/2 )×18
=144
分析:可以由等差数列性质,直接代入前n项和公式.
例 1:
解:
16
a2+a15
答:前16项的和为144
探究 等差数列的前n项和公式的其他形式
例
练习
等差数列 -10,-6,-2,2,…前多少项的和是54?
解:
n1=9,n2=-3
等差数列-10,-6,-2,2,…前9项的和是54.
例3:
设题中的等差数列为{an},前n项和是 sn,
则a1= -10,d= -6-(-10) = 4,设 sn=54,
根据等差数列前 n项和公式,得
又因为n要为正整数
(舍去)
c
解得a1=-1,d=1,
所以a100=-1+99×1=98.
∴a100=a10+90d=98.
探究 等差数列的前n项和公式的其他形式
( 注意 a 还可以是 0)
一个关于 的,没有 的“ ”
n
常数项
二次函数
b
a
a
b
已知一个等差数列的前10项的和是310,前20项的和是1220,求sn.
解:
s10=310,
s20=1 220
例 4:
=n2-8-(n-1)2+8
=2n-1.
这个公式非常重要,适合于所有的数列求和,并不是只适合于等差数列,需完全掌握。
小结
知三求二
