《直线与平面垂直的判定》课件
图片预览








文档简介
课件45张PPT。直线和平面垂直的判定(1)引入新课在直线和平面相交的位置关系中,有一种相交是很特殊的,我们把它叫做垂直相交,这节课我们重点来探究这种形式的相交直线与平面垂直观察实例,发现新知旗杆与地面的关系,给人以直线与平面垂直的形象。大桥的桥柱与水面的位置关系,给人以直线与平面垂直的形象。 观察实例,发现新知实例研探,定义新知探究:什么叫做直线和平面垂直呢?当直线与平面垂直时,此直线与平面内的所有直线的关系又怎样呢?一条直线与一个平面垂直的意义是什么?问题引入新课旗杆AB所在直线
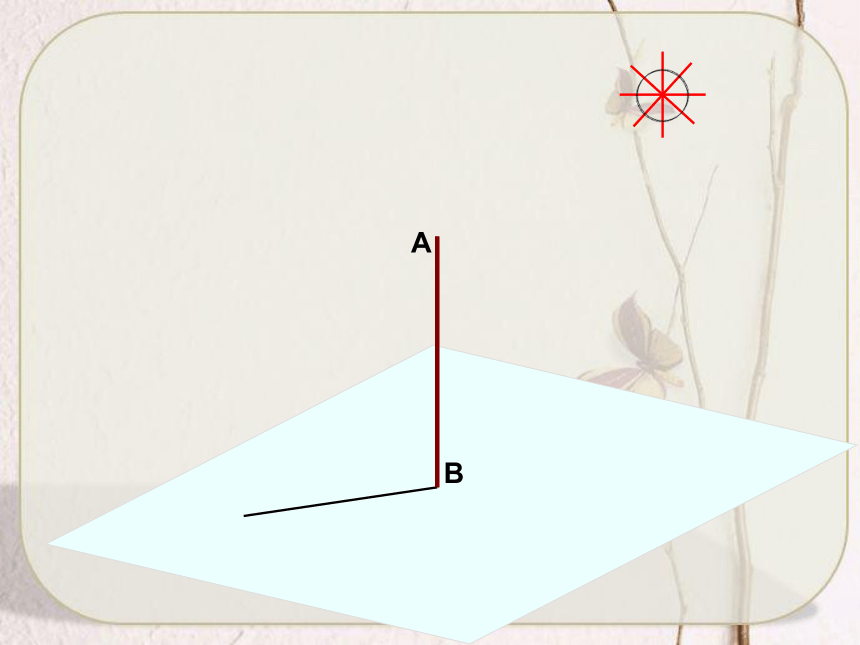
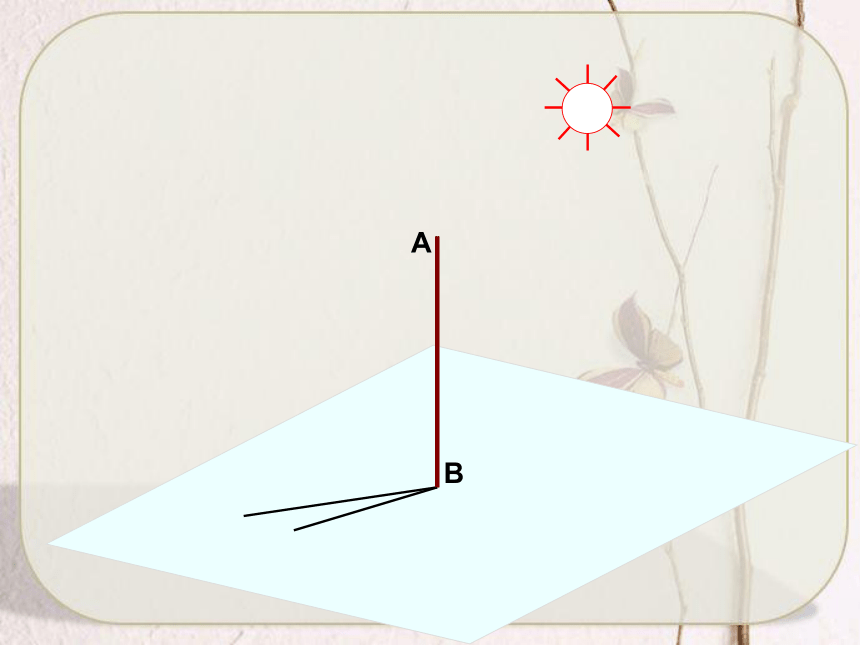
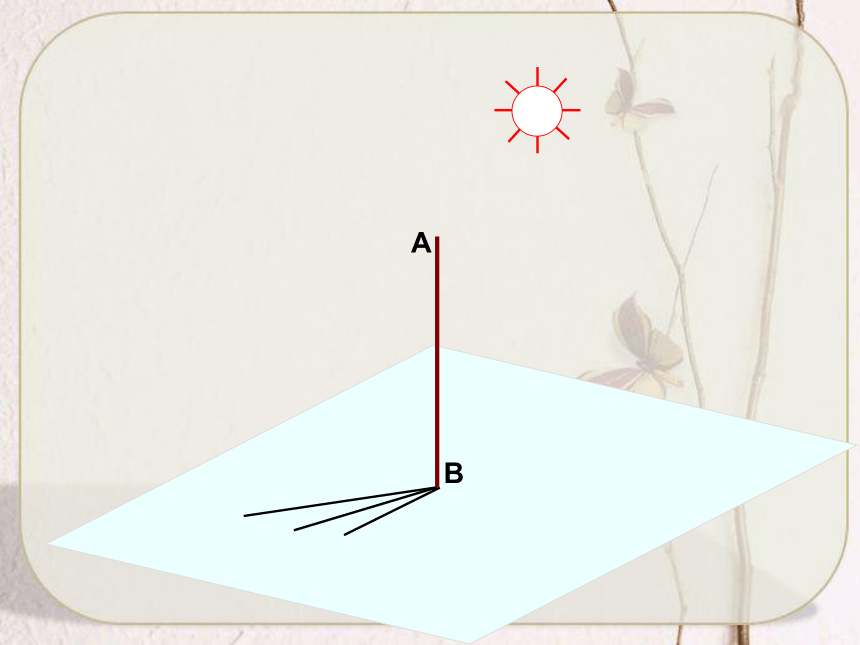
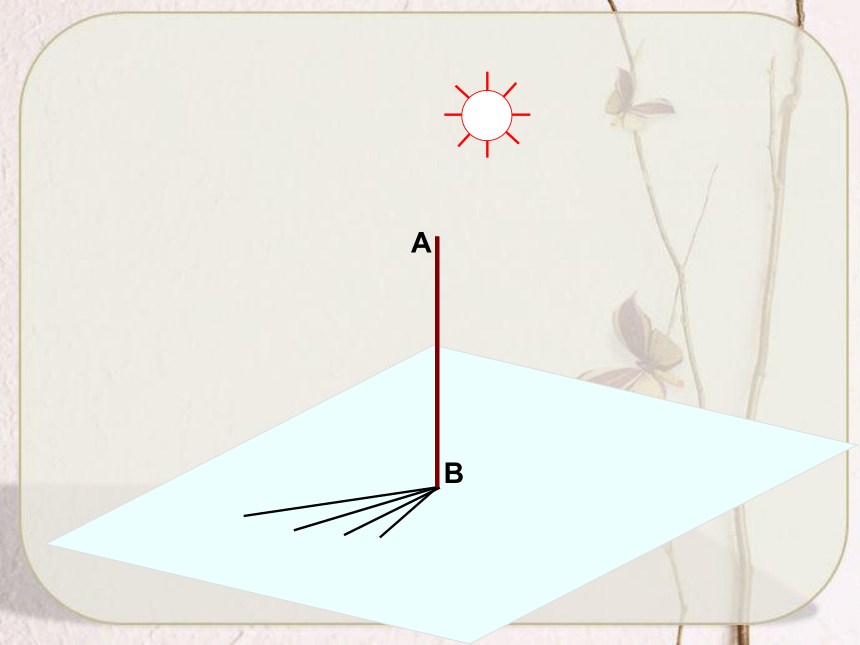
与地面内任意一条过点B的直线垂直. 与地面内任意一条不过点B的直线B1C1也垂直. 直线垂直于平面内的
任意一条直线.垂足定义直线与平面垂直 如果一条直线l 和一个平面α内的任意一条直
都垂直,我们就说直线l 和平面α互相垂直.
记作:l ⊥α画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直 1.如果一条直线 l 和一个平面内的无数条直线都垂直,则直线 l 和平面 α互相垂直( ) 思考:
? Bl线线垂直 线面垂直性质定理 直线 l 垂直于平面α ,则直线 l 垂直于平面α中的任意一条直线X直线与平面垂直 除定义外,如何判定一条直线与平面垂直呢?探究 如图,准备一块三角形的纸片,做一个试验: 过 的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC于桌面接触) 直线与平面垂直的判定定理:一条直线和一个平面内的两条相交直线都垂直,则这条直线垂直于这个平面.α线线垂直 线面垂直 例1. 如图,已知 ,求证 例2 已知:正方体中,AC是面对角线,BD'是与AC 异面的体对角线.
求证:AC⊥BD'
证明:连接BD
因为正方体ABCD-A'B'C'D'
所以DD‘⊥平面ABCD
又因为
所以
因为AC、BD 为对角线
所以AC⊥BD
因为DD'∩BD=D
所以AC⊥平面D'DB
所以AC⊥BD'
ABDCA′B′C′D′例3 在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB的中点,求证:(1)BC⊥平面PAB
(2) AD⊥PC. 如图,直四棱柱 (侧棱与底面垂直的棱柱称为直棱柱)中,底面四边形 满足什么条件时, ?答:底面四边形ABCD对角线相互垂直.探究巩固练习1.平行四边形ABCD所在平面a外有一点P,且PA=PB=PC=PD,求证:点P与平行四边形对角线交点O的连线PO垂直于AB、AD.巩固练习PABCO归纳小结今天这节课,我们学习了直线和平面垂直的定义,这个定义最初用在判定定理的证明上,但用得较多的则是,如果直线l垂直于平面a,那么l就垂直于a内的任何一条直线;对于判定定理,判定线、面垂直,实质是转化成线、线垂直,从中不难发现立体几何问题解决的一般思路?直线和平面垂直的判定(2)复习引入1.直线与平面垂直的定义如果直线l与平面α的任意一条直线都垂直,我们就说直线l与平面α互相垂直,记作l⊥α.2.直线与平面垂直的判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。引课我们知道,当直线和平面垂直时,该直线叫做平面的垂线。如果直线和平面不垂直,是不是也该给它取个名字呢?此时又该如何刻画直线和平面的这种关系呢?直线与平面所成的角1.平面的斜线如图,若一条直线PA和一个平面α相交,但不垂直,那么这条直线就叫做这个平面的斜线,斜线和平面的交点A叫做斜足。PA斜足斜线O斜线垂线一条直线垂直于平面,它们所成的角是90°一条直线和平面平行,或在平面内,它们所成的角是0°直线和平面所成角的范围是[0°,90°]第2个空间角斜线在平面上的射影 平面的一条斜线和它在平面内的射影所成的锐角,叫做这条直线和这个平面所成的角1.斜线与平面所成的角是指斜线和它在平面上的射影所成的角2.平面的垂线与平面所成的角为直角3. 一条直线与平面平行或在平面内,则这条直线与平面所成的角是00一条直线与平面所成的角的取值范围是重点说明例1 在Rt△ABC中,∠B=90°,P为△ABC所在平面外一点,PA⊥平面ABC(1)四面体P-ABC中有几个直角三角形(2)分别指出PB,PC与平面ABC所成的角
AC,PC与平面PAB所成的角ACBP 例2 在正方体ABCD-A1B1C1D1中.
(1)求直线A1B和平面ABCD所成的角;
(2)求直线D1B和平面BB1C1C所成的角的正弦值.D1ABA1CB1C1DAC1DCA1D1BF例3 在正方体ABCD—A1B1C1D1 中,求直线A1B与平面A1B1CD所成的角AC1DCBP变式:(1)求直线AC与平面A1B1CD所成的角(2)E,F分别是BC,CC1的中点,求EF与面ACC1A1所成的角.B1A1D1QB1EO巩固练习1.判断下列说法是否正确(1)两条平行直线在同一平面内的射影
一定是平行直线 ( )(2)两条相交直线在同一平面内的射影
一定是相交直线 ( )(3)两条异面直线在同一平面内的射影
要么是平行直线,要么是相交直线 ( )(4)若斜线段长相等,则它们在平面内
的射影长也相等 ( )
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影A1D1C1B1ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB0o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB90o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB45o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB30o巩固练习归纳小结1.直线与平面垂直的概念(1)利用定义;(2)利用判定定理.3.数学思想方法:转化的思想3.直线与平面垂直的判定垂直于平面内任意一条直线2. 线面角的概念及范围
与地面内任意一条过点B的直线垂直. 与地面内任意一条不过点B的直线B1C1也垂直. 直线垂直于平面内的
任意一条直线.垂足定义直线与平面垂直 如果一条直线l 和一个平面α内的任意一条直
都垂直,我们就说直线l 和平面α互相垂直.
记作:l ⊥α画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直 1.如果一条直线 l 和一个平面内的无数条直线都垂直,则直线 l 和平面 α互相垂直( ) 思考:
? Bl线线垂直 线面垂直性质定理 直线 l 垂直于平面α ,则直线 l 垂直于平面α中的任意一条直线X直线与平面垂直 除定义外,如何判定一条直线与平面垂直呢?探究 如图,准备一块三角形的纸片,做一个试验: 过 的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC于桌面接触) 直线与平面垂直的判定定理:一条直线和一个平面内的两条相交直线都垂直,则这条直线垂直于这个平面.α线线垂直 线面垂直 例1. 如图,已知 ,求证 例2 已知:正方体中,AC是面对角线,BD'是与AC 异面的体对角线.
求证:AC⊥BD'
证明:连接BD
因为正方体ABCD-A'B'C'D'
所以DD‘⊥平面ABCD
又因为
所以
因为AC、BD 为对角线
所以AC⊥BD
因为DD'∩BD=D
所以AC⊥平面D'DB
所以AC⊥BD'
ABDCA′B′C′D′例3 在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB的中点,求证:(1)BC⊥平面PAB
(2) AD⊥PC. 如图,直四棱柱 (侧棱与底面垂直的棱柱称为直棱柱)中,底面四边形 满足什么条件时, ?答:底面四边形ABCD对角线相互垂直.探究巩固练习1.平行四边形ABCD所在平面a外有一点P,且PA=PB=PC=PD,求证:点P与平行四边形对角线交点O的连线PO垂直于AB、AD.巩固练习PABCO归纳小结今天这节课,我们学习了直线和平面垂直的定义,这个定义最初用在判定定理的证明上,但用得较多的则是,如果直线l垂直于平面a,那么l就垂直于a内的任何一条直线;对于判定定理,判定线、面垂直,实质是转化成线、线垂直,从中不难发现立体几何问题解决的一般思路?直线和平面垂直的判定(2)复习引入1.直线与平面垂直的定义如果直线l与平面α的任意一条直线都垂直,我们就说直线l与平面α互相垂直,记作l⊥α.2.直线与平面垂直的判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。引课我们知道,当直线和平面垂直时,该直线叫做平面的垂线。如果直线和平面不垂直,是不是也该给它取个名字呢?此时又该如何刻画直线和平面的这种关系呢?直线与平面所成的角1.平面的斜线如图,若一条直线PA和一个平面α相交,但不垂直,那么这条直线就叫做这个平面的斜线,斜线和平面的交点A叫做斜足。PA斜足斜线O斜线垂线一条直线垂直于平面,它们所成的角是90°一条直线和平面平行,或在平面内,它们所成的角是0°直线和平面所成角的范围是[0°,90°]第2个空间角斜线在平面上的射影 平面的一条斜线和它在平面内的射影所成的锐角,叫做这条直线和这个平面所成的角1.斜线与平面所成的角是指斜线和它在平面上的射影所成的角2.平面的垂线与平面所成的角为直角3. 一条直线与平面平行或在平面内,则这条直线与平面所成的角是00一条直线与平面所成的角的取值范围是重点说明例1 在Rt△ABC中,∠B=90°,P为△ABC所在平面外一点,PA⊥平面ABC(1)四面体P-ABC中有几个直角三角形(2)分别指出PB,PC与平面ABC所成的角
AC,PC与平面PAB所成的角ACBP 例2 在正方体ABCD-A1B1C1D1中.
(1)求直线A1B和平面ABCD所成的角;
(2)求直线D1B和平面BB1C1C所成的角的正弦值.D1ABA1CB1C1DAC1DCA1D1BF例3 在正方体ABCD—A1B1C1D1 中,求直线A1B与平面A1B1CD所成的角AC1DCBP变式:(1)求直线AC与平面A1B1CD所成的角(2)E,F分别是BC,CC1的中点,求EF与面ACC1A1所成的角.B1A1D1QB1EO巩固练习1.判断下列说法是否正确(1)两条平行直线在同一平面内的射影
一定是平行直线 ( )(2)两条相交直线在同一平面内的射影
一定是相交直线 ( )(3)两条异面直线在同一平面内的射影
要么是平行直线,要么是相交直线 ( )(4)若斜线段长相等,则它们在平面内
的射影长也相等 ( )
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影A1D1C1B1ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB0o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB90o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB45o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB30o巩固练习归纳小结1.直线与平面垂直的概念(1)利用定义;(2)利用判定定理.3.数学思想方法:转化的思想3.直线与平面垂直的判定垂直于平面内任意一条直线2. 线面角的概念及范围
