24.1 锐角的三角函数—正切课件
图片预览




文档简介
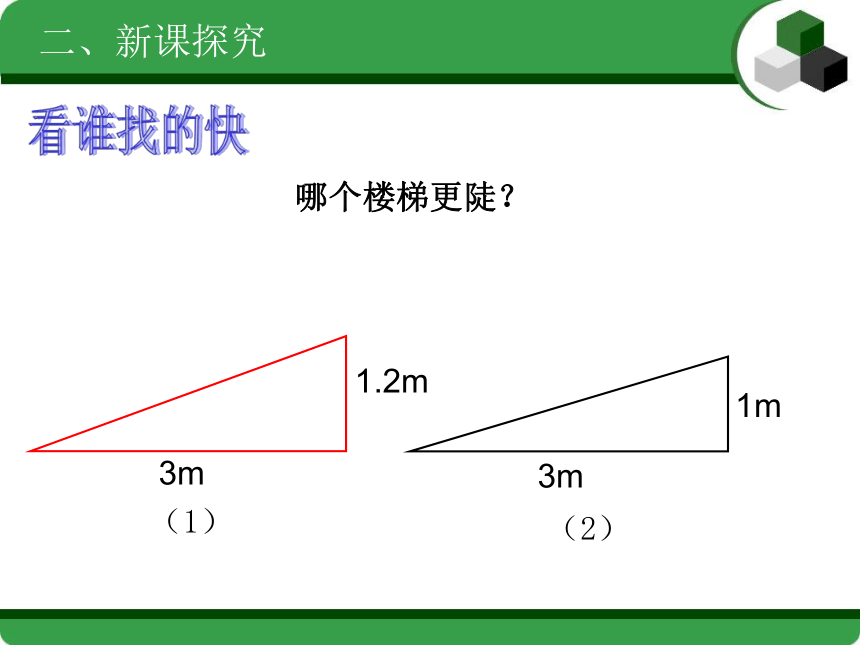
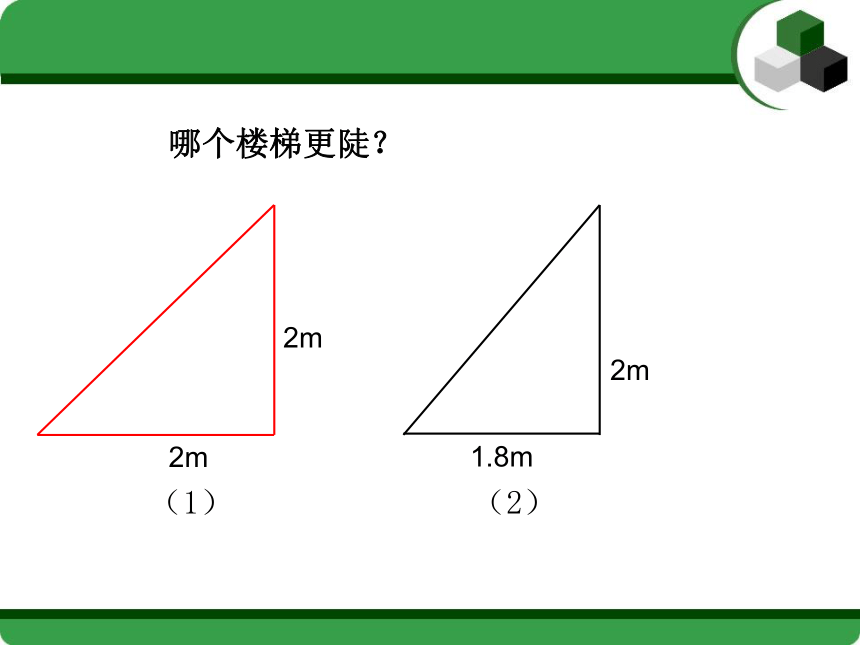
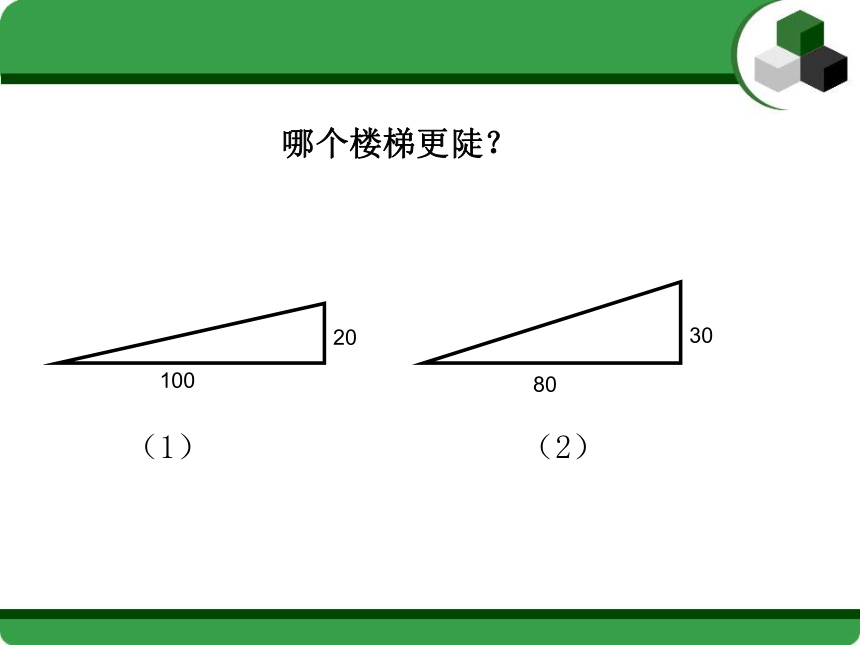
课件18张PPT。24.1 锐角的三角函数一、情境引入╮┌3m1.2m二、新课探究看谁找的快(1)(2)哪个楼梯更陡?2m2m(1)(2)哪个楼梯更陡?(1)(2)哪个楼梯更陡?10020如果角度不变,在 的一边上任取点B,自点B作
另一边的垂线,垂足为C。ABB1B2(1)Rt△AB1C1和Rt△ABC有什么关系?
由此你得出什么结论?在直角三角形中,若一个锐角的大小是一个定值,
那么这个锐角的对边与邻边的比值也随之确定.
定义:在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即1.tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.tanA是一个比值(直角边之比.注意比的顺序,且tanA﹥0,无单位.)
4.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角A度数越大,tanA值越大。
定义中需要注意的几个问题:用数学去解释生活如图,正切也经常用来描述山坡的坡度.例如,
有一山坡在水平方向上每前进100m就升高60m,
那么山坡的坡度i(即tanα)就是:
定义:坡面与水平面的夹角(α)称为坡角,坡面的铅直高度h与水平宽度l的比称为坡度i(或坡比),即坡度等于坡角的正切.例题讲解例1.如图,在ΔABC中AC=4,BC=3,∠C=90°
求tanA和tanB的值。变式:(1)在ΔABC中AB=4,BC=3,∠C=90°
求tanA和tanB的值。3.在等腰△ABC,AB=AC=13,BC=10,
求tanB.
4.某水库大坝的横断面是梯形ABCD,顶宽CD=5m,
坝高7m,迎水坡BC的坡度i1=1:2,背水坡AD的坡度
i2=1:1,求坝底宽AB及斜坡AD的坡角DABC课时小结本节课你学会了什么?1.如图, ∠C=90°CD⊥AB.试用三种方法表示tanB。┌B2.在上图中,若BD=6,CD=12.求tanA的值.
思考:布置作业基础训练24.1基础平台(一)
结束寄语锐角三角函数描述了直角三角形中边与角的关系,它又是一个变量之间重要的函数关系,即新奇,又富有魅力,你可要与它建立好感情噢!
另一边的垂线,垂足为C。ABB1B2(1)Rt△AB1C1和Rt△ABC有什么关系?
由此你得出什么结论?在直角三角形中,若一个锐角的大小是一个定值,
那么这个锐角的对边与邻边的比值也随之确定.
定义:在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即1.tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.tanA是一个比值(直角边之比.注意比的顺序,且tanA﹥0,无单位.)
4.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角A度数越大,tanA值越大。
定义中需要注意的几个问题:用数学去解释生活如图,正切也经常用来描述山坡的坡度.例如,
有一山坡在水平方向上每前进100m就升高60m,
那么山坡的坡度i(即tanα)就是:
定义:坡面与水平面的夹角(α)称为坡角,坡面的铅直高度h与水平宽度l的比称为坡度i(或坡比),即坡度等于坡角的正切.例题讲解例1.如图,在ΔABC中AC=4,BC=3,∠C=90°
求tanA和tanB的值。变式:(1)在ΔABC中AB=4,BC=3,∠C=90°
求tanA和tanB的值。3.在等腰△ABC,AB=AC=13,BC=10,
求tanB.
4.某水库大坝的横断面是梯形ABCD,顶宽CD=5m,
坝高7m,迎水坡BC的坡度i1=1:2,背水坡AD的坡度
i2=1:1,求坝底宽AB及斜坡AD的坡角DABC课时小结本节课你学会了什么?1.如图, ∠C=90°CD⊥AB.试用三种方法表示tanB。┌B2.在上图中,若BD=6,CD=12.求tanA的值.
思考:布置作业基础训练24.1基础平台(一)
结束寄语锐角三角函数描述了直角三角形中边与角的关系,它又是一个变量之间重要的函数关系,即新奇,又富有魅力,你可要与它建立好感情噢!
