《志鸿全优设计》2013-2014学年高中数学北师必修1单元目标检测:第三章 指数函数和对数函数(含解析)
文档属性
| 名称 | 《志鸿全优设计》2013-2014学年高中数学北师必修1单元目标检测:第三章 指数函数和对数函数(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-10 05:37:48 | ||
图片预览


文档简介
数学北师必修1第三章 指数函数和对数函数单元检测
(时间:120分钟,满分:150分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给定函数①,②,③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是( ).
A.①② B.②③ C.③④ D.①④
2.若0<x<y<1,则( ).
A.3y<3x B.logx3<logy3
C.log4x<log4y D.
3.下列各组函数,在同一直角坐标中,f(x)与g(x)有相同图像的一组是( ).
A.f(x)=,g(x)=
B.f(x)=,g(x)=x-3
C.f(x)=,g(x)=2log2x
D.f(x)=x,g(x)=lg 10x
4.若xlog23=1,则3x+9x的值为( ).
A.3 B. C.6 D.
5.若a<0,则函数y=(1-a)x-1的图像必过点( ).
A.(0,1) B.(0,0) C.(0,-1) D.(1,-1)
6.f(x)=lg(10x+1)+ax是偶函数,g(x)=是奇函数,那么a+b的值为( ).
A.1 B.-1 C. D.
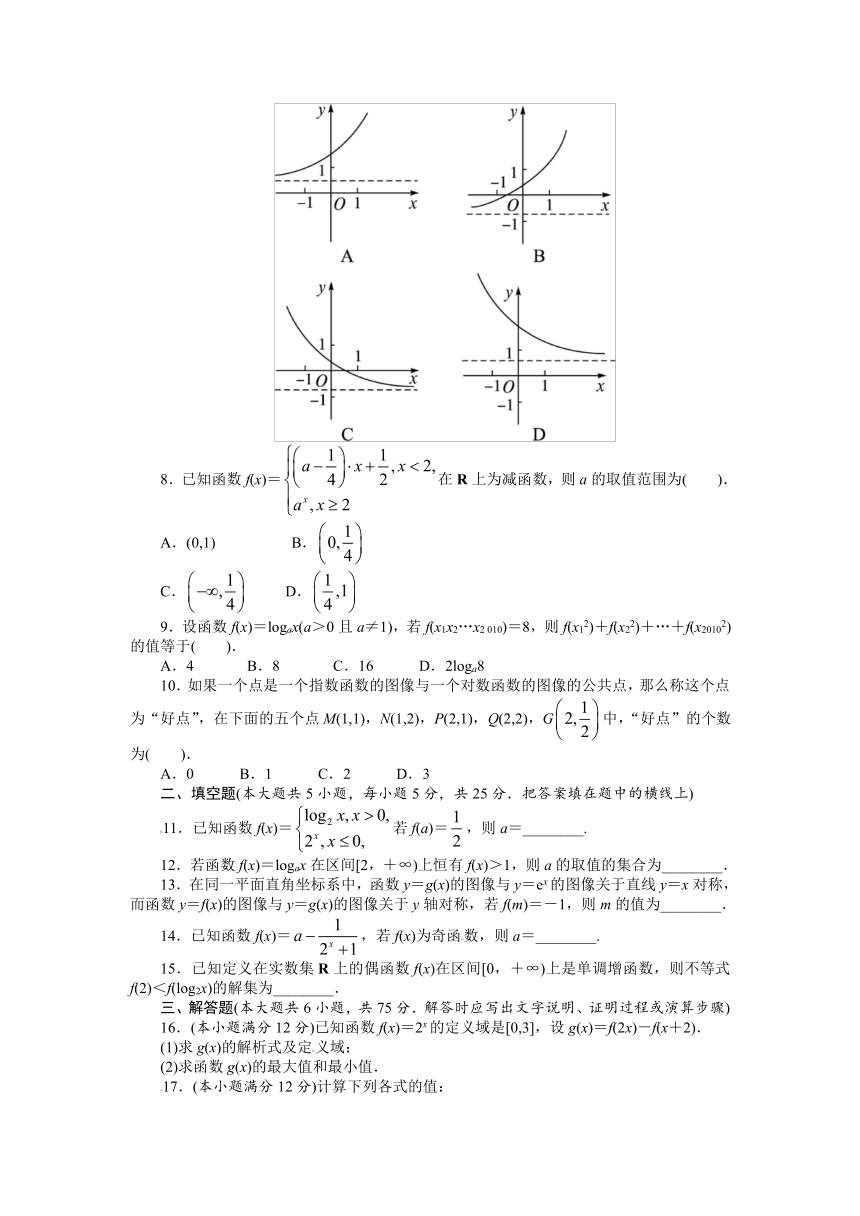
7.若函数f(x)=loga(x+b)(其中a,b为常数)的图像如下图所示,则函数g(x)=ax+b的大致图像是( ).
8.已知函数f(x)=在R上为减函数,则a的取值范围为( ).
A.(0,1) B.
C. D.
9.设函数f(x)=logax(a>0且a≠1),若f(x1x2…x2 010)=8,则f(x12)+f(x22)+…+f(x20102)的值等于( ).
A.4 B.8 C.16 D.2loga8
10.如果一个点是一个指数函数的图像与一个对数函数的图像的公共点,那么称这个点为“好点”,在下面的五个点M(1,1),N(1,2),P(2,1),Q(2,2),G中,“好点”的个数为( ).
A.0 B.1 C.2 D.3
二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)
11.已知函数f(x)=若f(a)=,则a=________.
12.若函数f(x)=logax在区间[2,+∞)上恒有f(x)>1,则a的取值的集合为________.
13.在同一平面直角坐标系中,函数y=g(x)的图像与y=ex的图像关于直线y=x对称,而函数y=f(x)的图像与y=g(x)的图像关于y轴对称,若f(m)=-1,则m的值为________.
14.已知函数f(x)=,若f(x)为奇函数,则a=________.
15.已知定义在实数集R上的偶函数f(x)在区间[0,+∞)上是单调增函数,则不等式f(2)<f(log2x)的解集为________.
三、解答题(本大题共6小题,共75分.解答时应写出文字说明、证明过程或演算步骤)
16.(本小题满分12分)已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2).
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
17.(本小题满分12分)计算下列各式的值:
(1);
(2).
18.(本小题满分12分)已知定义域为R的函数f(x)=是奇函数.
(1)求b的值;
(2)判断函数f(x)的单调性;
(3)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒立,求k的取值范围.
19.(本小题满分12分)已知函数f(x)=,
(1)若函数f(x)的值域为(-∞,-1],求实数a的值;
(2)若函数f(x)在(-∞,1]内为增函数,求实数a的取值范围.
20.(本小题满分13分)已知函数f(x)=log2(2x+1).
(1)求证:函数f(x)在(-∞,+∞)内单调递增;
(2)若关于x的方程log2(2x-1)=m+f(x)在[1,2]上有解,求m的取值范围.
21.(本小题满分14分)有一个湖泊受污染,其湖水的容量为V立方米,每天流入湖的水量等于流出湖的水量.现假设降雨量和蒸发量平衡,且污染物和湖水均匀混合.
用(P≥0),表示某一时刻一立方米湖水中所含污染物的克数(我们称其为湖水污染质量分数),g(0)表示湖水污染初始质量分数.
(1)当湖水污染质量分数为常数时,求湖水污染初始质量分数;
(2)分析g(0)<时,湖水的污染程度如何.
参考答案
1.B 点拨:和y=|x-1|在区间(0,1)上单调递减,和y=2x+1在区间(0,1)上单调递增.
2.C 点拨:∵y=3x在R上是增函数,且0<x<y<1,
∴3x<3y,故A错误.
∵y=log3x在(0,+∞)上是增函数,且0<x<y<1,
∴log3x<log3y<log31=0.
∴,即logx3>logy3,故B错误.
∵y=log4x在(0,+∞)上是增函数,且0<x<y<1,
∴log4x<log4y,故C正确.
∵在R上是减函数,且0<x<y<1,
∴,故D错误.
3.D 点拨:选项A中,f(x)的定义域为R,g(x)的定义域为[0,+∞);选项B中,f(x)的定义域为(-∞,-3)∪(-3,+∞),g(x)的定义域为R;选项C中,f(x)==x,x∈[0,+∞),g(x)=2log2x,x∈(0,+∞),定义域和对应关系都不同;选项D中,g(x)=lg 10x=xlg 10=x,故选D.
4.C 点拨:∵x·log23=1,
∴x==log32.
∴3x+9x=3x+ (3x)2==2+22=6.
5.B 点拨:根据指数函数y=ax恒过定点(0,1)知,函数y=(1-a)x-1恒过定点(0,0).
6.D 点拨:f(x)=lg(10x+1)+ax是偶函数,则lg(10x+1)+ax=lg(10-x+1)-ax2ax=lg(10-x+1)-lg(10x+1)=-lg(10x+1),∴2ax==-x(2a+1)x=0,∴.∵g(x)=是奇函数,故g(0)==0b=1.于是a+b=.
7.D 点拨:由题意知
∴则选D.
8.B 点拨:由,
得0<a<.
又f(x)在R上为减函数,需满足,即a2-2a≤0,a(a-2)≤0.∴0≤a≤2.综上,知0<a<.
9.C 点拨:f(x12)+f(x22))+…+f(x20102)
=logax12+logax22+…+logax20102
=loga(12·x22·…·x20102)
=loga(x1x2…x2 010)2
=2loga(x1x2…x2 010)
=2f(x1x2…x2 010)=2×8=16.
10.C 点拨:∵指数函数过定点(0,1),对数函数过定点(1,0),
∴指数函数不过(1,1),(2,1)点,对数函数不过点(1,2).
∴点M,N,P一定不是好点.
可验证:过指数函数,且过对数函数y=log4x.Q(2,2)在和的图像上.
11.或-1 点拨:当a>0时,若f(a)=,则log2a=,∴;
当a≤0时,若f(a)=,则2a=,∴a=-1.
综上可知,或a=-1.
12.{a|1<a<2} 点拨:若函数f(x)=logax在区间[2,+∞)上恒有f(x)>1,则,即.∴1<a<2.
13. 点拨:由题意知y=g(x)应为y=ex的反函数,即y=g(x)=ln x,而y=f(x)与y=g(x)=ln x的图像关于y轴对称,故可得y=f(x)=ln(-x),又f(m)=-1,所以ln(-m)=-1,得-m=e-1,即.
14. 点拨:函数f(x)的定义域为R,若f(x)为奇函数,则f(0)=0,即,∴.
15.∪(4,+∞) 点拨:因为函数f(x)在区间[0,+∞)上是单调增函数,且f(2)<f(log2x),所以2<log2x,解得x>4;因为函数f(x)为偶函数,所以log2x<-2,解得0<x<,所以不等式f(2)<f(log2x)的解集为∪(4,+∞).
16.解:(1)∵f(x)=2x,∴g(x)=f(2x)-f(x+2)=22x-2x+2.
∵f(x)的定义域是[0,3],
∴解得0≤x≤1.
∴g(x)的定义域是[0,1].
(2)g(x)=(2x)2-4×2x
=(2x-2)2-4.
∵x∈[0,1],
∴2x∈[1,2].
∴当2x=1,即x=0时,g(x)取得最大值-3;
当2x=2,即x=1时,g(x)取得最小值-4.
17.解:(1)原式=
=
=
=.
(2)原式=log2.52.52+lg 10-2+
.
18.解:(1)∵f(x)在定义域R上是奇函数,∴f(0)=0,即,∴b=1.
(2)由(1)知f(x)=,
设x1<x2,则f(x1)-f(x2)=.
∵函数y=2x在R上是增函数且x1<x2,
∴.
又,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在(-∞,+∞)上为减函数.
(3)因f(x)是奇函数,从而不等式f(t2-2t)+f(2t2-k)<0,
等价于f(t2-2t)<-f(2t2-k)=f(k-2t2),
因f(x)为减函数,由上式推得t2-2t>k-2t2.
即对一切t∈R有3t2-2t-k>0,
从而判别式Δ=4+12k<0k<.
19.解:(1)设g(x)=x2-2ax+3=(x-a)2+3-a2.
∵f(x)的值域为(-∞,-1],
∴,即,
∴g(x)≥2.
由3-a2=2,得a=1或a=-1.
(2)要使f(x)在(-∞,1]内是增函数,需g(x)在(-∞,1]上为减函数且g(x)>0对于x∈(-∞,1]恒成立,
∴,即.
∴1≤a<2.
故实数a的取值范围是[1,2).
20.(1)证明:任取x1<x2,则
f(x1)-f(x2)=
=,
∵x1<x2,∴.
∴,.
∴f(x1)<f(x2),即函数f(x)在(-∞,+∞)内单调递增.
(2)∵m=log2(2x-1)-log2(2x+1)
,
当1≤x≤2时,,
∴.
∴m的取值范围是.
21.解:(1)当湖水污染质量分数g(t)为常数时,g(t)的值与t无关,故有g(0)-=0,
∴g(0)=,即湖水污染初始质量分数为.
(2)当g(0)<时,g(0)-<0.
又∵随t的增大逐渐增大,∴g(t)为减函数.故湖水的污染程度越来越轻.
(时间:120分钟,满分:150分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给定函数①,②,③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是( ).
A.①② B.②③ C.③④ D.①④
2.若0<x<y<1,则( ).
A.3y<3x B.logx3<logy3
C.log4x<log4y D.
3.下列各组函数,在同一直角坐标中,f(x)与g(x)有相同图像的一组是( ).
A.f(x)=,g(x)=
B.f(x)=,g(x)=x-3
C.f(x)=,g(x)=2log2x
D.f(x)=x,g(x)=lg 10x
4.若xlog23=1,则3x+9x的值为( ).
A.3 B. C.6 D.
5.若a<0,则函数y=(1-a)x-1的图像必过点( ).
A.(0,1) B.(0,0) C.(0,-1) D.(1,-1)
6.f(x)=lg(10x+1)+ax是偶函数,g(x)=是奇函数,那么a+b的值为( ).
A.1 B.-1 C. D.
7.若函数f(x)=loga(x+b)(其中a,b为常数)的图像如下图所示,则函数g(x)=ax+b的大致图像是( ).
8.已知函数f(x)=在R上为减函数,则a的取值范围为( ).
A.(0,1) B.
C. D.
9.设函数f(x)=logax(a>0且a≠1),若f(x1x2…x2 010)=8,则f(x12)+f(x22)+…+f(x20102)的值等于( ).
A.4 B.8 C.16 D.2loga8
10.如果一个点是一个指数函数的图像与一个对数函数的图像的公共点,那么称这个点为“好点”,在下面的五个点M(1,1),N(1,2),P(2,1),Q(2,2),G中,“好点”的个数为( ).
A.0 B.1 C.2 D.3
二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)
11.已知函数f(x)=若f(a)=,则a=________.
12.若函数f(x)=logax在区间[2,+∞)上恒有f(x)>1,则a的取值的集合为________.
13.在同一平面直角坐标系中,函数y=g(x)的图像与y=ex的图像关于直线y=x对称,而函数y=f(x)的图像与y=g(x)的图像关于y轴对称,若f(m)=-1,则m的值为________.
14.已知函数f(x)=,若f(x)为奇函数,则a=________.
15.已知定义在实数集R上的偶函数f(x)在区间[0,+∞)上是单调增函数,则不等式f(2)<f(log2x)的解集为________.
三、解答题(本大题共6小题,共75分.解答时应写出文字说明、证明过程或演算步骤)
16.(本小题满分12分)已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2).
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
17.(本小题满分12分)计算下列各式的值:
(1);
(2).
18.(本小题满分12分)已知定义域为R的函数f(x)=是奇函数.
(1)求b的值;
(2)判断函数f(x)的单调性;
(3)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒立,求k的取值范围.
19.(本小题满分12分)已知函数f(x)=,
(1)若函数f(x)的值域为(-∞,-1],求实数a的值;
(2)若函数f(x)在(-∞,1]内为增函数,求实数a的取值范围.
20.(本小题满分13分)已知函数f(x)=log2(2x+1).
(1)求证:函数f(x)在(-∞,+∞)内单调递增;
(2)若关于x的方程log2(2x-1)=m+f(x)在[1,2]上有解,求m的取值范围.
21.(本小题满分14分)有一个湖泊受污染,其湖水的容量为V立方米,每天流入湖的水量等于流出湖的水量.现假设降雨量和蒸发量平衡,且污染物和湖水均匀混合.
用(P≥0),表示某一时刻一立方米湖水中所含污染物的克数(我们称其为湖水污染质量分数),g(0)表示湖水污染初始质量分数.
(1)当湖水污染质量分数为常数时,求湖水污染初始质量分数;
(2)分析g(0)<时,湖水的污染程度如何.
参考答案
1.B 点拨:和y=|x-1|在区间(0,1)上单调递减,和y=2x+1在区间(0,1)上单调递增.
2.C 点拨:∵y=3x在R上是增函数,且0<x<y<1,
∴3x<3y,故A错误.
∵y=log3x在(0,+∞)上是增函数,且0<x<y<1,
∴log3x<log3y<log31=0.
∴,即logx3>logy3,故B错误.
∵y=log4x在(0,+∞)上是增函数,且0<x<y<1,
∴log4x<log4y,故C正确.
∵在R上是减函数,且0<x<y<1,
∴,故D错误.
3.D 点拨:选项A中,f(x)的定义域为R,g(x)的定义域为[0,+∞);选项B中,f(x)的定义域为(-∞,-3)∪(-3,+∞),g(x)的定义域为R;选项C中,f(x)==x,x∈[0,+∞),g(x)=2log2x,x∈(0,+∞),定义域和对应关系都不同;选项D中,g(x)=lg 10x=xlg 10=x,故选D.
4.C 点拨:∵x·log23=1,
∴x==log32.
∴3x+9x=3x+ (3x)2==2+22=6.
5.B 点拨:根据指数函数y=ax恒过定点(0,1)知,函数y=(1-a)x-1恒过定点(0,0).
6.D 点拨:f(x)=lg(10x+1)+ax是偶函数,则lg(10x+1)+ax=lg(10-x+1)-ax2ax=lg(10-x+1)-lg(10x+1)=-lg(10x+1),∴2ax==-x(2a+1)x=0,∴.∵g(x)=是奇函数,故g(0)==0b=1.于是a+b=.
7.D 点拨:由题意知
∴则选D.
8.B 点拨:由,
得0<a<.
又f(x)在R上为减函数,需满足,即a2-2a≤0,a(a-2)≤0.∴0≤a≤2.综上,知0<a<.
9.C 点拨:f(x12)+f(x22))+…+f(x20102)
=logax12+logax22+…+logax20102
=loga(12·x22·…·x20102)
=loga(x1x2…x2 010)2
=2loga(x1x2…x2 010)
=2f(x1x2…x2 010)=2×8=16.
10.C 点拨:∵指数函数过定点(0,1),对数函数过定点(1,0),
∴指数函数不过(1,1),(2,1)点,对数函数不过点(1,2).
∴点M,N,P一定不是好点.
可验证:过指数函数,且过对数函数y=log4x.Q(2,2)在和的图像上.
11.或-1 点拨:当a>0时,若f(a)=,则log2a=,∴;
当a≤0时,若f(a)=,则2a=,∴a=-1.
综上可知,或a=-1.
12.{a|1<a<2} 点拨:若函数f(x)=logax在区间[2,+∞)上恒有f(x)>1,则,即.∴1<a<2.
13. 点拨:由题意知y=g(x)应为y=ex的反函数,即y=g(x)=ln x,而y=f(x)与y=g(x)=ln x的图像关于y轴对称,故可得y=f(x)=ln(-x),又f(m)=-1,所以ln(-m)=-1,得-m=e-1,即.
14. 点拨:函数f(x)的定义域为R,若f(x)为奇函数,则f(0)=0,即,∴.
15.∪(4,+∞) 点拨:因为函数f(x)在区间[0,+∞)上是单调增函数,且f(2)<f(log2x),所以2<log2x,解得x>4;因为函数f(x)为偶函数,所以log2x<-2,解得0<x<,所以不等式f(2)<f(log2x)的解集为∪(4,+∞).
16.解:(1)∵f(x)=2x,∴g(x)=f(2x)-f(x+2)=22x-2x+2.
∵f(x)的定义域是[0,3],
∴解得0≤x≤1.
∴g(x)的定义域是[0,1].
(2)g(x)=(2x)2-4×2x
=(2x-2)2-4.
∵x∈[0,1],
∴2x∈[1,2].
∴当2x=1,即x=0时,g(x)取得最大值-3;
当2x=2,即x=1时,g(x)取得最小值-4.
17.解:(1)原式=
=
=
=.
(2)原式=log2.52.52+lg 10-2+
.
18.解:(1)∵f(x)在定义域R上是奇函数,∴f(0)=0,即,∴b=1.
(2)由(1)知f(x)=,
设x1<x2,则f(x1)-f(x2)=.
∵函数y=2x在R上是增函数且x1<x2,
∴.
又,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在(-∞,+∞)上为减函数.
(3)因f(x)是奇函数,从而不等式f(t2-2t)+f(2t2-k)<0,
等价于f(t2-2t)<-f(2t2-k)=f(k-2t2),
因f(x)为减函数,由上式推得t2-2t>k-2t2.
即对一切t∈R有3t2-2t-k>0,
从而判别式Δ=4+12k<0k<.
19.解:(1)设g(x)=x2-2ax+3=(x-a)2+3-a2.
∵f(x)的值域为(-∞,-1],
∴,即,
∴g(x)≥2.
由3-a2=2,得a=1或a=-1.
(2)要使f(x)在(-∞,1]内是增函数,需g(x)在(-∞,1]上为减函数且g(x)>0对于x∈(-∞,1]恒成立,
∴,即.
∴1≤a<2.
故实数a的取值范围是[1,2).
20.(1)证明:任取x1<x2,则
f(x1)-f(x2)=
=,
∵x1<x2,∴.
∴,.
∴f(x1)<f(x2),即函数f(x)在(-∞,+∞)内单调递增.
(2)∵m=log2(2x-1)-log2(2x+1)
,
当1≤x≤2时,,
∴.
∴m的取值范围是.
21.解:(1)当湖水污染质量分数g(t)为常数时,g(t)的值与t无关,故有g(0)-=0,
∴g(0)=,即湖水污染初始质量分数为.
(2)当g(0)<时,g(0)-<0.
又∵随t的增大逐渐增大,∴g(t)为减函数.故湖水的污染程度越来越轻.
