14.2.2 完全平方公式(第2课时)课件(共19张PPT)
文档属性
| 名称 | 14.2.2 完全平方公式(第2课时)课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 21:49:42 | ||
图片预览





文档简介
(共19张PPT)
14.2.2完全平方公式
(第2课时)
人教版 八年级上册
教学目标
【教学目标】
1.类比去括号掌握添括号法则;
2.会用添括号法则,进行多项式的变形计算.
【重点】类比去括号掌握添括号法则.
【难点】会用添括号法则,进行多项式的变形计算.
复习回顾
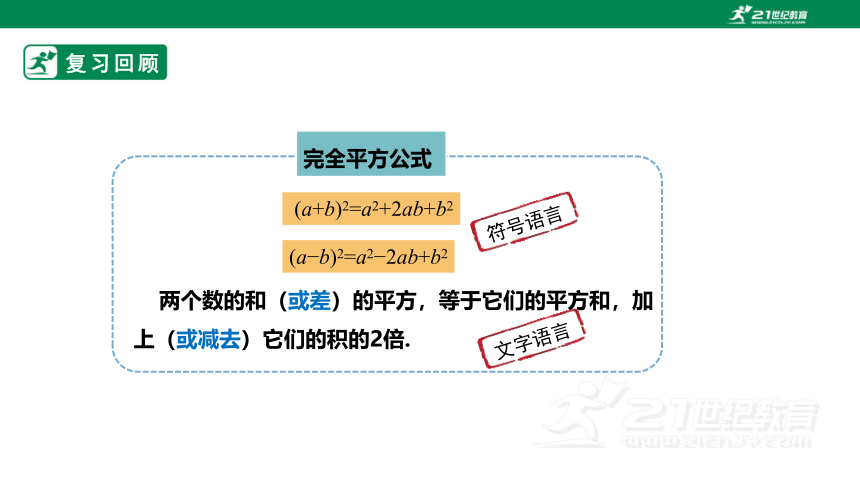
完全平方公式
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
符号语言
文字语言
复习回顾
你还记得去括号的法则吗?
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
去括号法则
新知探究
将等号左右两边对换,等式仍然成立.
a+b+c
=
a+(b+c)
a b c
=
a (b+c)
你能类比去括号法则
总结出添括号法则吗?
(1) a+(b+c)=________ (2) a-(b+c)=________
a+b+c
a-b-c
练一练:
新知探究
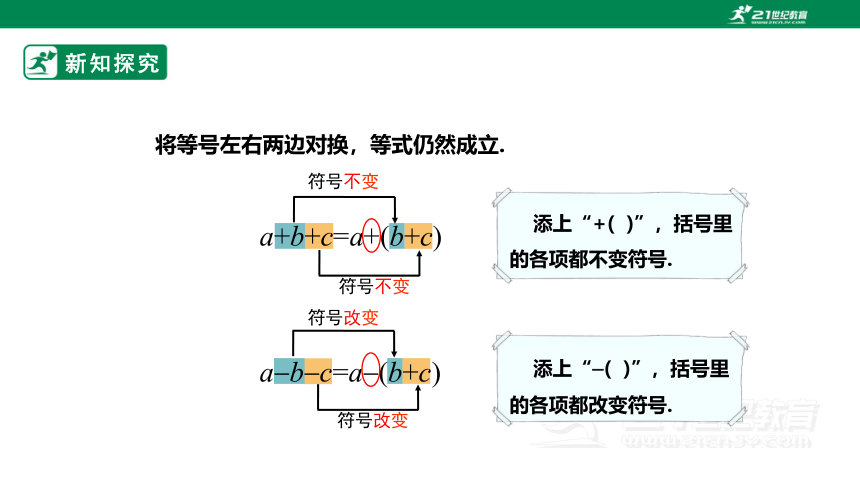
将等号左右两边对换,等式仍然成立.
a+b+c=a+(b+c)
a b c=a (b+c)
符号不变
符号不变
添上“+( )”,括号里的各项都不变符号.
符号改变
符号改变
添上“ ( )”,括号里的各项都改变符号.
新知探究
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
添括号法则
针对训练
在等号右边的括号内填上合适的项.
(1) a+b c=a+( );
(2) a b+c=a ( );
(3) 2a 2b c=2a ( );
(4) 2x+3y 2=2x+( ).
b c
b c
2b+c
3y 2
括号前面是正号,括到括号里的各项都不变符号.
括号前面是负号,括到括号里的各项都改变符号.
新知探究
添括号法则的巧记及添括号时“三注意”
1.法则巧记:遇“+”不变,遇“-”都变.
2.添括号时“三注意”:
(1)哪些项需要放进括号里面去;
(2)这些项在放进括号前是什么符号;
(3)所添括号前是什么符号.
新知探究
例5.运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) (2) (a+b+c)2
解:(1) (x+2y-3)(x-2y+3)
=[(x+(2y-3)][(x-(2y-3)]
=x2-(2y-3)2
=x2-(4y2-12y+9)
=x2-4y2+12y-9
(2) (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc
新知探究
(a+b+c)2
=[a+(b+c)]2
=a2+2a(b+c)+(b+c)2
=a2+b2+c2+2ab+2ac+2bc
(a+b+c)2
=[b+(a+c)]2
=b2+2b(a+c)+(a+c)2
=a2+b2+c2+2ab+2ac+2bc
(a+b+c)2 =a2+b2+c2+2ab+2ac+2bc
完全平方公式的推广
课堂练习
1.在下列去括号或添括号的变形中,错误的是( )
A. a-(b-c)=a-b+c B. a-(-b+c)=a-b-c
C. a-b-c=a-(b+c) D. a-b+c-d=a-(b-c+d)
2.3ab-4bc+1=3ab-( ), 括号中所填入的整式应是( )
A. -4bc+1 B.4bc+1 C.4bc-1 D. -4bc-1
B
C
课堂练习
3.为了应用平方差公式计算(x+3y-1)(x-3y+1),下列变形正确的是( )
A.[x-(3y+1)]2
B.[x+(3y+1)]2
C.[x+(3y-1)] [x-(3y-1)]
D.[(x-3y)+1)] [(x-3y)-1)]
C
课堂练习
4.灵活运用乘法公式计算:
已知(m+n+1)(m+n 1)=63,则m+n= .
解:∵ (m+n+1)(m+n 1)
=(m+n)2 12=63
∴(m+n)2=64
∴m+n= 8
8
课堂练习
5.运用乘法公式计算:
(1) (x-3y+1)2 (2) (3a+b-c) (3a-b+c) (3) 29×31×(302+1)
解:(1)原式=[(x-3y) +1]2
=(x-3y)2+2(x-3y) + 12
=x2- 6xy+9y2+2x-6y+1
(2)原式=[3a+(b-c)][(3a-(b-c)]
=9a2-(b-c)2
=9a2- (b2-2bc+c2)
=9a2- b2+ 2bc-c2
(3)原式=(30-1) × (30+1) × (302+1)
= (302-1) × (302+1)
= (302)2-12
=9002-1
=810000-1
=809999
课堂练习
6.计算:
解:
=
=
=8xy+6x+12y+18
课堂小结
注意:
添括号法则:
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;
如果括号前面是负号,括到括号里的各项都改变符号.
有些整式相乘需要先通过添括号作适当变形,然后再灵活运用乘法公式计算.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.2.2完全平方公式
(第2课时)
人教版 八年级上册
教学目标
【教学目标】
1.类比去括号掌握添括号法则;
2.会用添括号法则,进行多项式的变形计算.
【重点】类比去括号掌握添括号法则.
【难点】会用添括号法则,进行多项式的变形计算.
复习回顾
完全平方公式
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
符号语言
文字语言
复习回顾
你还记得去括号的法则吗?
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
去括号法则
新知探究
将等号左右两边对换,等式仍然成立.
a+b+c
=
a+(b+c)
a b c
=
a (b+c)
你能类比去括号法则
总结出添括号法则吗?
(1) a+(b+c)=________ (2) a-(b+c)=________
a+b+c
a-b-c
练一练:
新知探究
将等号左右两边对换,等式仍然成立.
a+b+c=a+(b+c)
a b c=a (b+c)
符号不变
符号不变
添上“+( )”,括号里的各项都不变符号.
符号改变
符号改变
添上“ ( )”,括号里的各项都改变符号.
新知探究
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
添括号法则
针对训练
在等号右边的括号内填上合适的项.
(1) a+b c=a+( );
(2) a b+c=a ( );
(3) 2a 2b c=2a ( );
(4) 2x+3y 2=2x+( ).
b c
b c
2b+c
3y 2
括号前面是正号,括到括号里的各项都不变符号.
括号前面是负号,括到括号里的各项都改变符号.
新知探究
添括号法则的巧记及添括号时“三注意”
1.法则巧记:遇“+”不变,遇“-”都变.
2.添括号时“三注意”:
(1)哪些项需要放进括号里面去;
(2)这些项在放进括号前是什么符号;
(3)所添括号前是什么符号.
新知探究
例5.运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) (2) (a+b+c)2
解:(1) (x+2y-3)(x-2y+3)
=[(x+(2y-3)][(x-(2y-3)]
=x2-(2y-3)2
=x2-(4y2-12y+9)
=x2-4y2+12y-9
(2) (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc
新知探究
(a+b+c)2
=[a+(b+c)]2
=a2+2a(b+c)+(b+c)2
=a2+b2+c2+2ab+2ac+2bc
(a+b+c)2
=[b+(a+c)]2
=b2+2b(a+c)+(a+c)2
=a2+b2+c2+2ab+2ac+2bc
(a+b+c)2 =a2+b2+c2+2ab+2ac+2bc
完全平方公式的推广
课堂练习
1.在下列去括号或添括号的变形中,错误的是( )
A. a-(b-c)=a-b+c B. a-(-b+c)=a-b-c
C. a-b-c=a-(b+c) D. a-b+c-d=a-(b-c+d)
2.3ab-4bc+1=3ab-( ), 括号中所填入的整式应是( )
A. -4bc+1 B.4bc+1 C.4bc-1 D. -4bc-1
B
C
课堂练习
3.为了应用平方差公式计算(x+3y-1)(x-3y+1),下列变形正确的是( )
A.[x-(3y+1)]2
B.[x+(3y+1)]2
C.[x+(3y-1)] [x-(3y-1)]
D.[(x-3y)+1)] [(x-3y)-1)]
C
课堂练习
4.灵活运用乘法公式计算:
已知(m+n+1)(m+n 1)=63,则m+n= .
解:∵ (m+n+1)(m+n 1)
=(m+n)2 12=63
∴(m+n)2=64
∴m+n= 8
8
课堂练习
5.运用乘法公式计算:
(1) (x-3y+1)2 (2) (3a+b-c) (3a-b+c) (3) 29×31×(302+1)
解:(1)原式=[(x-3y) +1]2
=(x-3y)2+2(x-3y) + 12
=x2- 6xy+9y2+2x-6y+1
(2)原式=[3a+(b-c)][(3a-(b-c)]
=9a2-(b-c)2
=9a2- (b2-2bc+c2)
=9a2- b2+ 2bc-c2
(3)原式=(30-1) × (30+1) × (302+1)
= (302-1) × (302+1)
= (302)2-12
=9002-1
=810000-1
=809999
课堂练习
6.计算:
解:
=
=
=8xy+6x+12y+18
课堂小结
注意:
添括号法则:
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;
如果括号前面是负号,括到括号里的各项都改变符号.
有些整式相乘需要先通过添括号作适当变形,然后再灵活运用乘法公式计算.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
