3.6 共点力的平衡条件及其应用 课件 高一上学期物理粤教版(2019)必修第一册(共29张PPT)
文档属性
| 名称 | 3.6 共点力的平衡条件及其应用 课件 高一上学期物理粤教版(2019)必修第一册(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 417.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-17 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
第六节 共点力的平衡条件及应用
一、共点力作用下物体的平衡
1.平衡态
(1)静止:物体的 和 都等于零的状态.
(2)匀速直线运动:物体的 不为零,其 为零的 状态.
2.平衡条件
(1)物体所受合外力为零,即F合=0.
(2)若采用正交分解法,平衡条件表达式为Fx=0,Fy=0.
速度
加速度
速度
加速度
3.物体平衡条件的相关推论
(1)二力平衡:如果物体在两个共点力的作用下处于平衡状
态,这两个力必定大小 ,方向 .
(2)三力平衡:如果物体在三个共点力的作用下处于平衡状
态,其中任意两个力的合力一定与第三个力大小 、
方向 .
(3)多力平衡:如果物体受多个力作用处于平衡,其中任何
一个力与其余力的合力大小 ,方向 .
相等
相反
相反
相等
相反
相等
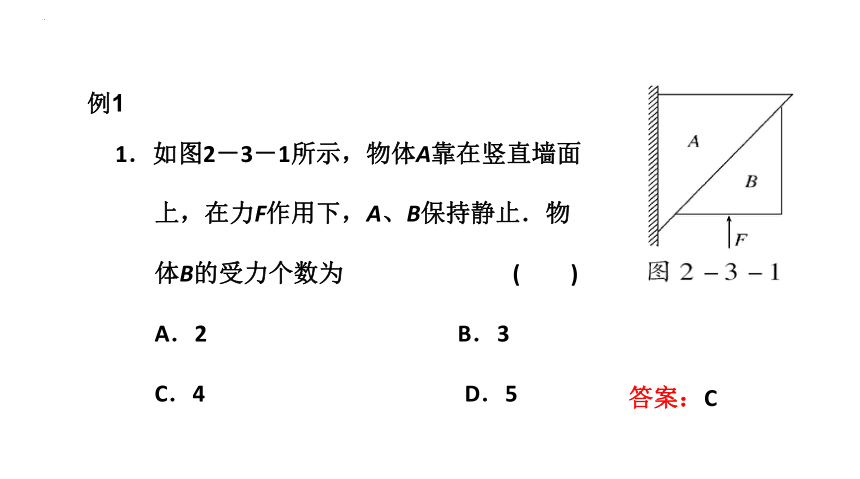
1.如图2-3-1所示,物体A靠在竖直墙面
上,在力F作用下,A、B保持静止.物
体B的受力个数为 ( )
A.2 B.3
C.4 D.5
答案:C
例1
解析:A能静止地靠在墙上,A、B之间
必有弹力,故B受重力、外力F与A对B
的弹力,为了B保持静止,必受A给的
摩擦力,如图所示,所以B受力个数为4个.C项正确.
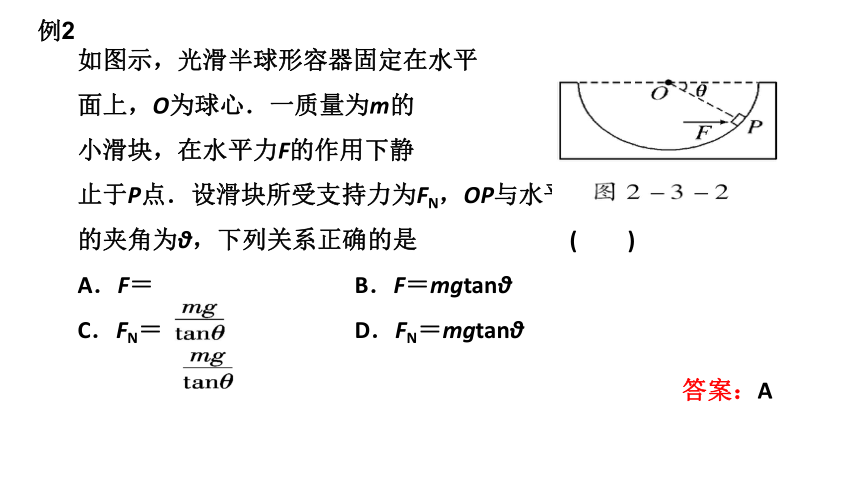
如图示,光滑半球形容器固定在水平
面上,O为球心.一质量为m的
小滑块,在水平力F的作用下静
止于P点.设滑块所受支持力为FN,OP与水平方向
的夹角为θ,下列关系正确的是 ( )
A.F= B.F=mgtanθ
C.FN= D.FN=mgtanθ
答案:A
例2
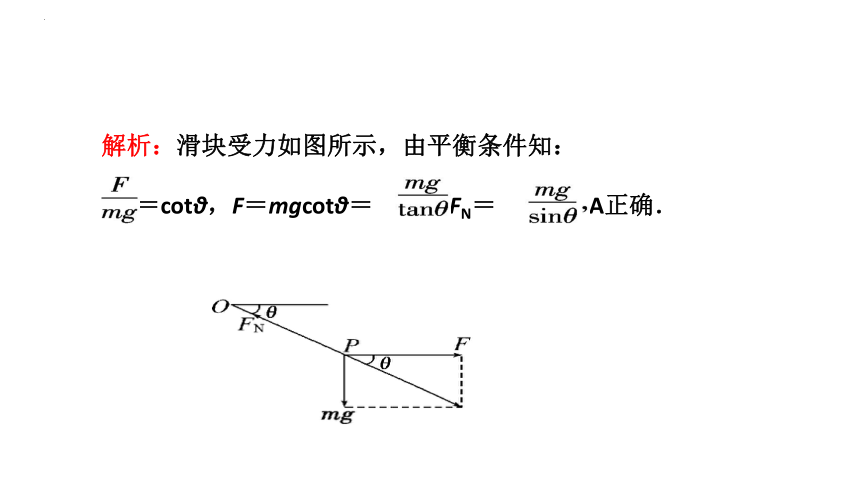
解析:滑块受力如图所示,由平衡条件知:
=cotθ,F=mgcotθ= ,FN= 故A正确.
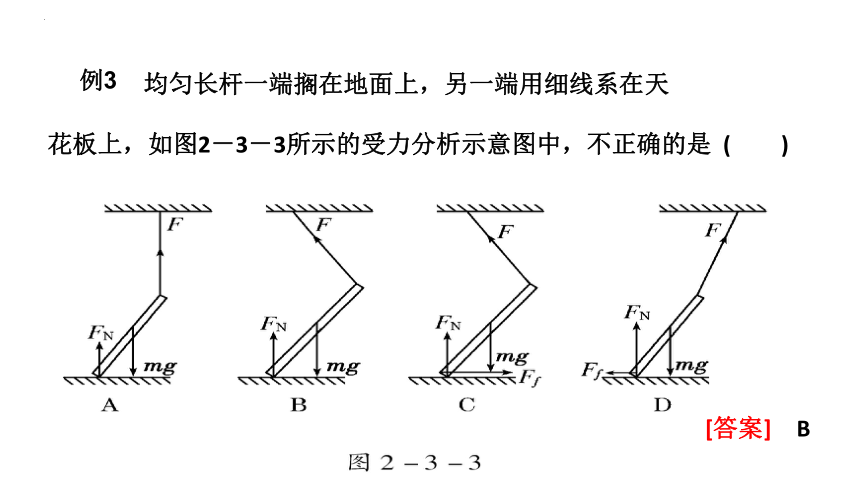
均匀长杆一端搁在地面上,另一端用细线系在天
花板上,如图2-3-3所示的受力分析示意图中,不正确的是 ( )
[答案] B
例3
长杆处于平衡状态,其所受所有外力的合力为零,即水平方向和竖直方向的合力都要为零,显然选项A正确;B、C、D选项中,将F沿水平和竖直方向分解,水平方向满足平衡条件的还有C、D选项.综上可知,选项A、C、D正确.
例4. (广东省实验中学模拟)
如图2-3-5所示,质量为m的正方体和
质量为M的正方体放在两竖直墙和水平面
间,处于静止状态.m与M相接触的边与
竖直方向的夹角为α,若不计一切摩擦,
求:
(1)水平面对正方体M的弹力大小;
(2)墙面对正方体m的弹力大小.
[解题样板] (1)以两个正方体整体为研究对象,整体受到向上的支持力和向下的重力,处于静止状态.┄┄┄(4分)
所以水平面对正方体M的弹力大小为
FN=(M+m)g┄┄┄┄┄┄┄(2分)
(2)对正方体m进行受力分析如图
2-3-6所示.┄┄┄┄┄┄┄┄┄(2分)
把FN2沿水平方向和竖直方向分解有
FN2cosα=FN1┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(2分)
FN2sinα=mg ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(2分)
解得FN1=mgcotα ┄┄┄┄┄┄┄┄┄┄┄┄┄┄ (2分)
[答案] (1)(M+m)g (2)mgcotα
练习
1.物体在共点力的作用下,下列说法中正确的是( )
A.物体的速度在某一时刻等于零,物体就一定处于平衡状态
B.物体相对于另一物体保持静止,物体一定处于平衡状态
C.物体所受合力为零,物体一定处于平衡状态
D.物体做匀加速运动时,物体处于平衡状态
答案:C
解析:某一时刻速度为零的物体,受力不一定为零,故不一定处于平衡状态,A错;物体相对于另一物体静止时,该物体不一定静止,如当另一物体做变速运动时,该物体也做变速运动,此物体处于非平衡状态,故B错;C选项符合平衡条件的判断,为正确选项;物体做匀加速运动,所受合力不为零,故不是平衡状态,D错.
2 .如图2-3-7所示,
质量为m的等边三棱柱静止在水平
放置的斜面上.已知三棱柱与斜面
之间的动摩擦因数为μ,斜面的倾角为30°,则斜面对三
棱柱的支持力与摩擦力的大小分别为 ( )
A. mg和 mg B. mg和 mg
C. mg和 μmg D. mg和 μmg
答案:A
解析: 三棱柱受重力、斜面的支持力和摩擦力三力平衡,
故FN=mgcosθ= mg,Ff=mgsinθ= mg,A选项正确.
3.如图2-3-8所示,物体A在竖直向上
的拉力F的作用下能静止在斜面上,关于A受力的个数,
下列说法中正确的是 ( )
A.A一定受两个力作用
B.A一定受四个力作用
C.A可能受三个力作用
D.A不是受两个力作用就是受四个力作用
答案:D
解析:若拉力F大小等于物体的重力,则物体A仅受F与G两个力的作用处于平衡状态;若F小于G,则物体A受到拉力F、重力G、斜面对它的垂直于斜面向上的支持力FN和沿斜面向上的静摩擦力Ff四个力处于平衡状态,所以D项正确.
4.如图2-3-9所示,一个半径为R、重为G的小球,用长
度为R的细绳悬挂在光滑的竖直墙壁上.用FT表示绳子
对球的拉力,用FN表示墙对球的支持力,下列结果中正
确的是 ( )
A.FT= G,FN=2G
B.FT= G,FN= G
C.FT= G,FN=
D.FT= G,FN=
答案:B
解析:以小球为研究对象,受力分析如图所示,由小球的半径为R和长度为R的细绳,可知夹角θ=30°,可求得FT=
FN=Gtan30°= G
故选B.
5.如图2-3-10所示,人重600 N,木块A重400 N,人与
A、A与地面的动摩擦因数均为0.2,现人用水平力拉绳,
使他与木块一起向右做匀速直线运动,滑轮摩擦不计,
求:
(1)人对绳的拉力;
(2)人脚对木块A的摩擦力的方向和大小.
答案:(1)100 N (2)方向向右 100 N
解析:设绳子的拉力为FT,地面对木块的摩擦力为FfA.
(1)取人和木块为整体,并对其进行受力分析,如图甲所示,由题意可知
FfA=μ(mA+m人)g=200 N.
由于系统处于平衡状态,故
2FT=FfA,
所以FT=100 N.
(2)取人为研究对象,对其进行受力分析,
如图乙所示.
由于人处于平衡状态,故FT=Ff人=100 N.
由于人与木块A处于相对静止状态,故人与木块A之间的摩擦力为静摩擦力.由牛顿第三定律可知人脚对木块的摩擦力为静摩擦力,方向向右,大小为100 N.
6.(双项)质量为m的木块在与水平方向成θ角的推力F的作用下,在水平地面上作匀速运动,已知木块与地面间的摩擦因数为μ,那么木块受到的滑动摩擦力为:
A. μmg
B. μ(mg+Fsinθ)
C. μ(mg-Fsinθ)
D. Fcosθ
θ
此题答案:
B、D
7.在竖直墙壁上,用斜向上的恒力按着一重为G的木块沿墙壁作匀速运动,F与竖直方向的夹角为θ,求滑动摩擦因数μ。
N
F
G
f
f
N
F
G
θ
此题答案:
8.如图所示,斜面倾角θ,木块M和斜面间滑动摩擦因数为μ,问物体m质量多大时,才能使木块匀速运动?。
此题答案:
M
m
θ
9.三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物,如图示。其中OB是水平的,A端、B端固定。若逐渐增加C端所挂物体的质量,则最先断的绳:
A.必定是OA ;
B.必定是OB;
C.必定是OC ;
D.可能是OB,也可能是OC 。
A
O B
C
A
10.如图所示,质量为m的物体放在倾角为θ的斜面上,它与斜面的滑动摩擦因数为μ,在水平推力的作用下,物体沿斜面向上匀速滑动,则物体所受的摩擦力为:
A.μmgcosθ
B.μ(mgcosθ+Fsinθ)
C.μ(mgcosθ-Fsinθ)
D. Fcosθ-mgsinθ
θ
此题答案:
B、C
——当物体处于平衡状态时,它所受的某一个力与它受的其余的力的合力等值反向。
重要推论
共点力的平衡解题方法小结
1.正确选取研究对象
2.隔离物体,分析物体的受力,画出受力图
3.根据作用效果,准确进行力的分解
4.根据平衡条件,列方程求解
第六节 共点力的平衡条件及应用
一、共点力作用下物体的平衡
1.平衡态
(1)静止:物体的 和 都等于零的状态.
(2)匀速直线运动:物体的 不为零,其 为零的 状态.
2.平衡条件
(1)物体所受合外力为零,即F合=0.
(2)若采用正交分解法,平衡条件表达式为Fx=0,Fy=0.
速度
加速度
速度
加速度
3.物体平衡条件的相关推论
(1)二力平衡:如果物体在两个共点力的作用下处于平衡状
态,这两个力必定大小 ,方向 .
(2)三力平衡:如果物体在三个共点力的作用下处于平衡状
态,其中任意两个力的合力一定与第三个力大小 、
方向 .
(3)多力平衡:如果物体受多个力作用处于平衡,其中任何
一个力与其余力的合力大小 ,方向 .
相等
相反
相反
相等
相反
相等
1.如图2-3-1所示,物体A靠在竖直墙面
上,在力F作用下,A、B保持静止.物
体B的受力个数为 ( )
A.2 B.3
C.4 D.5
答案:C
例1
解析:A能静止地靠在墙上,A、B之间
必有弹力,故B受重力、外力F与A对B
的弹力,为了B保持静止,必受A给的
摩擦力,如图所示,所以B受力个数为4个.C项正确.
如图示,光滑半球形容器固定在水平
面上,O为球心.一质量为m的
小滑块,在水平力F的作用下静
止于P点.设滑块所受支持力为FN,OP与水平方向
的夹角为θ,下列关系正确的是 ( )
A.F= B.F=mgtanθ
C.FN= D.FN=mgtanθ
答案:A
例2
解析:滑块受力如图所示,由平衡条件知:
=cotθ,F=mgcotθ= ,FN= 故A正确.
均匀长杆一端搁在地面上,另一端用细线系在天
花板上,如图2-3-3所示的受力分析示意图中,不正确的是 ( )
[答案] B
例3
长杆处于平衡状态,其所受所有外力的合力为零,即水平方向和竖直方向的合力都要为零,显然选项A正确;B、C、D选项中,将F沿水平和竖直方向分解,水平方向满足平衡条件的还有C、D选项.综上可知,选项A、C、D正确.
例4. (广东省实验中学模拟)
如图2-3-5所示,质量为m的正方体和
质量为M的正方体放在两竖直墙和水平面
间,处于静止状态.m与M相接触的边与
竖直方向的夹角为α,若不计一切摩擦,
求:
(1)水平面对正方体M的弹力大小;
(2)墙面对正方体m的弹力大小.
[解题样板] (1)以两个正方体整体为研究对象,整体受到向上的支持力和向下的重力,处于静止状态.┄┄┄(4分)
所以水平面对正方体M的弹力大小为
FN=(M+m)g┄┄┄┄┄┄┄(2分)
(2)对正方体m进行受力分析如图
2-3-6所示.┄┄┄┄┄┄┄┄┄(2分)
把FN2沿水平方向和竖直方向分解有
FN2cosα=FN1┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(2分)
FN2sinα=mg ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(2分)
解得FN1=mgcotα ┄┄┄┄┄┄┄┄┄┄┄┄┄┄ (2分)
[答案] (1)(M+m)g (2)mgcotα
练习
1.物体在共点力的作用下,下列说法中正确的是( )
A.物体的速度在某一时刻等于零,物体就一定处于平衡状态
B.物体相对于另一物体保持静止,物体一定处于平衡状态
C.物体所受合力为零,物体一定处于平衡状态
D.物体做匀加速运动时,物体处于平衡状态
答案:C
解析:某一时刻速度为零的物体,受力不一定为零,故不一定处于平衡状态,A错;物体相对于另一物体静止时,该物体不一定静止,如当另一物体做变速运动时,该物体也做变速运动,此物体处于非平衡状态,故B错;C选项符合平衡条件的判断,为正确选项;物体做匀加速运动,所受合力不为零,故不是平衡状态,D错.
2 .如图2-3-7所示,
质量为m的等边三棱柱静止在水平
放置的斜面上.已知三棱柱与斜面
之间的动摩擦因数为μ,斜面的倾角为30°,则斜面对三
棱柱的支持力与摩擦力的大小分别为 ( )
A. mg和 mg B. mg和 mg
C. mg和 μmg D. mg和 μmg
答案:A
解析: 三棱柱受重力、斜面的支持力和摩擦力三力平衡,
故FN=mgcosθ= mg,Ff=mgsinθ= mg,A选项正确.
3.如图2-3-8所示,物体A在竖直向上
的拉力F的作用下能静止在斜面上,关于A受力的个数,
下列说法中正确的是 ( )
A.A一定受两个力作用
B.A一定受四个力作用
C.A可能受三个力作用
D.A不是受两个力作用就是受四个力作用
答案:D
解析:若拉力F大小等于物体的重力,则物体A仅受F与G两个力的作用处于平衡状态;若F小于G,则物体A受到拉力F、重力G、斜面对它的垂直于斜面向上的支持力FN和沿斜面向上的静摩擦力Ff四个力处于平衡状态,所以D项正确.
4.如图2-3-9所示,一个半径为R、重为G的小球,用长
度为R的细绳悬挂在光滑的竖直墙壁上.用FT表示绳子
对球的拉力,用FN表示墙对球的支持力,下列结果中正
确的是 ( )
A.FT= G,FN=2G
B.FT= G,FN= G
C.FT= G,FN=
D.FT= G,FN=
答案:B
解析:以小球为研究对象,受力分析如图所示,由小球的半径为R和长度为R的细绳,可知夹角θ=30°,可求得FT=
FN=Gtan30°= G
故选B.
5.如图2-3-10所示,人重600 N,木块A重400 N,人与
A、A与地面的动摩擦因数均为0.2,现人用水平力拉绳,
使他与木块一起向右做匀速直线运动,滑轮摩擦不计,
求:
(1)人对绳的拉力;
(2)人脚对木块A的摩擦力的方向和大小.
答案:(1)100 N (2)方向向右 100 N
解析:设绳子的拉力为FT,地面对木块的摩擦力为FfA.
(1)取人和木块为整体,并对其进行受力分析,如图甲所示,由题意可知
FfA=μ(mA+m人)g=200 N.
由于系统处于平衡状态,故
2FT=FfA,
所以FT=100 N.
(2)取人为研究对象,对其进行受力分析,
如图乙所示.
由于人处于平衡状态,故FT=Ff人=100 N.
由于人与木块A处于相对静止状态,故人与木块A之间的摩擦力为静摩擦力.由牛顿第三定律可知人脚对木块的摩擦力为静摩擦力,方向向右,大小为100 N.
6.(双项)质量为m的木块在与水平方向成θ角的推力F的作用下,在水平地面上作匀速运动,已知木块与地面间的摩擦因数为μ,那么木块受到的滑动摩擦力为:
A. μmg
B. μ(mg+Fsinθ)
C. μ(mg-Fsinθ)
D. Fcosθ
θ
此题答案:
B、D
7.在竖直墙壁上,用斜向上的恒力按着一重为G的木块沿墙壁作匀速运动,F与竖直方向的夹角为θ,求滑动摩擦因数μ。
N
F
G
f
f
N
F
G
θ
此题答案:
8.如图所示,斜面倾角θ,木块M和斜面间滑动摩擦因数为μ,问物体m质量多大时,才能使木块匀速运动?。
此题答案:
M
m
θ
9.三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物,如图示。其中OB是水平的,A端、B端固定。若逐渐增加C端所挂物体的质量,则最先断的绳:
A.必定是OA ;
B.必定是OB;
C.必定是OC ;
D.可能是OB,也可能是OC 。
A
O B
C
A
10.如图所示,质量为m的物体放在倾角为θ的斜面上,它与斜面的滑动摩擦因数为μ,在水平推力的作用下,物体沿斜面向上匀速滑动,则物体所受的摩擦力为:
A.μmgcosθ
B.μ(mgcosθ+Fsinθ)
C.μ(mgcosθ-Fsinθ)
D. Fcosθ-mgsinθ
θ
此题答案:
B、C
——当物体处于平衡状态时,它所受的某一个力与它受的其余的力的合力等值反向。
重要推论
共点力的平衡解题方法小结
1.正确选取研究对象
2.隔离物体,分析物体的受力,画出受力图
3.根据作用效果,准确进行力的分解
4.根据平衡条件,列方程求解
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
