青岛版数学九年级上册 2.5 解直角三角形的应用(共3课时) 教案(表格式)
文档属性
| 名称 | 青岛版数学九年级上册 2.5 解直角三角形的应用(共3课时) 教案(表格式) |  | |
| 格式 | doc | ||
| 文件大小 | 171.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 10:08:29 | ||
图片预览



文档简介
2.5 解直角三角形的应用
教学目标 理解仰角、俯角的意义,准确运用这些概念来解决一些实际问题。培养学生将实际问题抽象成数学模型并进行解释与应用的能力。在探究学习过程中,注重培养学生的合作交流意识,激发学生学习数学的兴趣。
教学重点 理解仰角和俯角的概念。
教学难点 能解与直角三角形有关的实际问题。
第一课时
教学过程 教师活动 学生活动
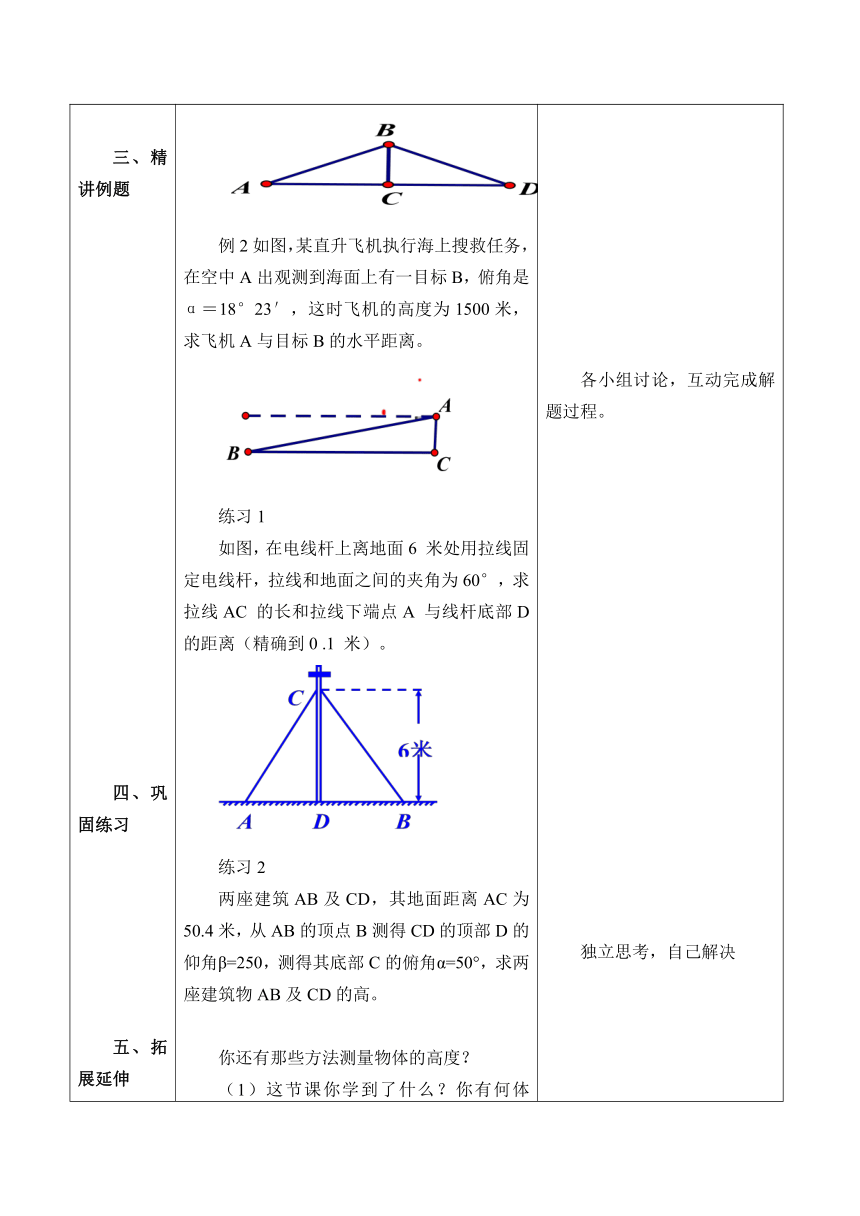
一、课前延伸二、课内探究三、精讲例题四、巩固练习五、拓展延伸 1、仰角和俯角在实际测量时,从低处观测高出的目标时,( )与( )所成的锐角叫做仰角;从高出观测低处的目标时,( )与( ) 所成的锐角叫做俯角。2、解决直角三角形的应用思路。(1)把实际问题转化为解直角三角形的问题,关键是找出实际问题中的 ( ),直角三角形( )之间的关系,是解决与直角三角形有关的实际问题的重要工具。(2)解答过程的思路:1、创设问题情景,引出新知:上海东方明珠塔于1994 年10 月1 日建成,出示图片,在各国广播电视塔的排名榜中,当时其高度列亚洲第一、世界第三。与外滩的“万国建筑博览群”隔江相望。在塔顶俯瞰上海风景,美不胜收。运用本章所学过的知识,能测出东方明珠塔的高度来吗?2、探究新知:(1)认识仰角与俯角:想要解决刚才的问题,我们先来了解仰角、俯角的概念,利用多媒体演示仰角、俯角。(2)引导学生小组探究解决导入中提出的问题。为了测量东方明珠塔的高度,同学们在距离东方明珠塔200 米处的地面上,用高1.20 米的测角仪测得东方明珠塔顶的仰角为60°48 ′。根据测量的结果,小亮画了一张示意图,其中 ( ) 表示东方明珠塔,( ) 为测角仪的支架,DC= ( )米,CB= ( )米,∠ADE= ( )。根据在前一学段学过的长方形对边相等的有关知识,你能求出AB 的长吗?例1如图,厂房屋顶人字架的跨度为10米,上弦AB=BD,∠A=260,求中柱BC和上弦AB的长(精确到0.01米)例2如图,某直升飞机执行海上搜救任务,在空中A出观测到海面上有一目标B,俯角是α=18°23′,这时飞机的高度为1500米,求飞机A与目标B的水平距离。练习1 如图,在电线杆上离地面6 米处用拉线固定电线杆,拉线和地面之间的夹角为60°,求拉线AC 的长和拉线下端点A 与线杆底部D 的距离(精确到0 .1 米)。 练习2两座建筑AB及CD,其地面距离AC为50.4米,从AB的顶点B测得CD的顶部D的仰角β=250,测得其底部C的俯角α=50°,求两座建筑物AB及CD的高。你还有那些方法测量物体的高度?(1)这节课你学到了什么?你有何体会?(2)这节课你还存在什么问题? 思考回答思考回答思考回答各小组讨论,互动完成解题过程。独立思考,自己解决畅所欲言,总结所学所得
第二课时
教学目标 1.学会解直角三角形在实际问题中的应用; 2.提高学生观察、分析、综合解决问题的能力。3.增强学生创新意识,培养学生学习能力;体验数学在实际生活中的应用;渗透理论联系实际的辩证唯物主义思想。
教学重点 解直角三角形在测量方面的应用。
教学难点 综合应用知识程度较高的例3.
教学过程 教师活动 学生活动
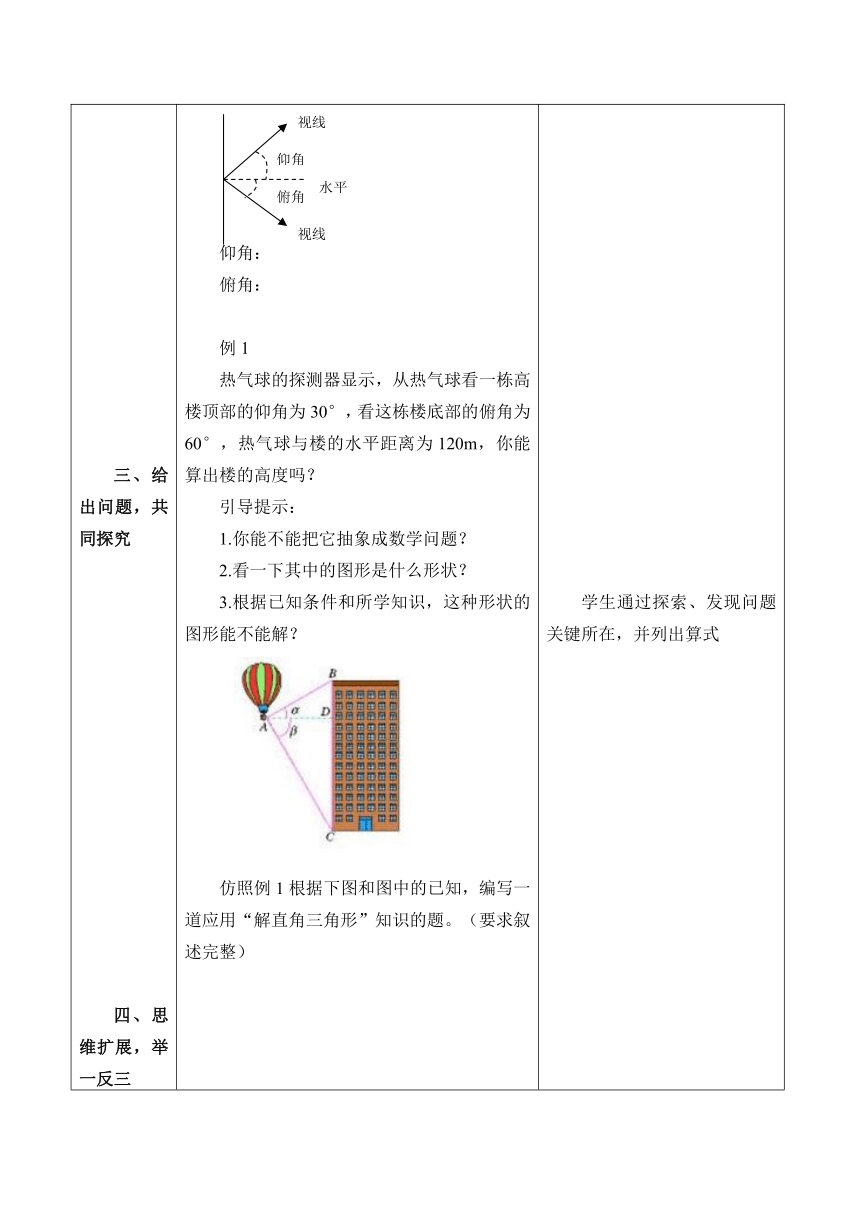
一、复习提问,加深理解二、提出问题,引入新课三、给出问题,共同探究四、思维扩展,举一反三五、巩固提高 六、扩展延伸,再进一步 1.直角三角形共有几个元素构成?它们分别是什么?2.什么是解直角三角形?3.如何解直角三角形呢?三边关系:两锐角的关系:边角关系: 我们在生活中,观看一个较高的物体需要抬起头来往上看,用一个词语来描述叫做什么?(仰视)那低下头看一个物体又怎么描述呢?(俯视)那么,我们来看一下这个分析图: 仰角:俯角:例1热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120m,你能算出楼的高度吗?引导提示:1.你能不能把它抽象成数学问题?2.看一下其中的图形是什么形状?3.根据已知条件和所学知识,这种形状的图形能不能解?仿照例1根据下图和图中的已知,编写一道应用“解直角三角形”知识的题。(要求叙述完整)例2如图,河对岸有水塔AB.在C处测得塔顶A的仰角为30°,向塔前进12m到达D,在D处测得A的仰角为45°,求塔高。 引导:AB同时属于哪两个三角形?这两个三角形又已知了什么条件呢?是否可用这两个条件来表示出其它的边呢?如何表示?CD和CB有什么关系呢?现在你能列出一个方程来求AB了吗?如何列?请计算。BC—BD=CD ,CD=12 m,即AB/tg30°-AB/tg45°=12(不唯一)教师总结(1)利用解直角三角形解决实际问题。(2)测量问题中的两种模式。 积极思考、踊跃回答回答问题并学习新知识学生通过探索、发现问题关键所在,并列出算式通过编写题目来加深学生对解直角三角形应用的理解与掌握,达到扩散思维的作用1、积极思考,踊跃回答,并计算结果。2、四人小组讨论,给出结果。
第三课时
教学目标 1.明确方位角、坡角、坡度的概念,并能将之灵活应用于实际生活。2.能熟练运用解直角三角形的有关知识来解决实际应用问题。3.会解决底部不能到达的物件高度的测量问题。
教学重点 能熟练运用解直角三角形的有关知识来解决实际应用问题。
教学难点 底部不能到达的物件高度的测量问题。
教学过程 教师活动 学生活动
一、学前准备二、自学探究三、练习自测四、拓展延伸五、归纳小结 指南或指北的 方向与目标方向线构成小于900的角,叫做__ ____,如图:点A在点O的___________,点B在点O的南偏西45 或 方向。2阅读课本有关坡度的内容,说一说什么是坡角,什么是坡度或坡比,坡度与坡角的正切有什么关系? 请把重点知识写在下面。______________________________________________________________________________1.某地计划在河流的上游修建一条拦水大坝,大坝的横断面ABCD是梯形(如图),坝顶宽BC=6米,坝高25米,应水坡AB的坡度i=1:3,被水坡CD的坡度i=1:2.5.(1)求斜坡AB和CD的长(精确到0.01米);(2)。求拦水大坝的底面AD的宽。 2.要测量铁塔的高AB,在地面上选取一点C,在AC两点间选取一点D,测得CD=14米,在C,D两点处分别用测角仪测得铁塔顶端B的仰角为α=300和β=450. 测角仪支架的高为1.2米,求铁塔的高(精确到0.1米)3.如图,一船从A点出发,沿北偏东方向航行12海里到达B点,然后又沿南偏东方向航行16海里到达C点,那么从C点再航行多远才能直接返回出发点A(精确到0.1海里)1.一名滑雪运动员从坡度为1:5的山坡上滑下,如果这名运动员滑行的距离为150米,那么他下降的高度是多少(精确到0.1米)?2.如上图,拦水坝的横断面为梯形ABCD,根据图中数据,求:(1)角α和β的大小(精确到 )(2)坝底宽AD和斜坡AB的长(精确到0.1米)3.入夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位,一条船在松花江某水段自西向东沿直线航行,在A处测得航标C在北偏东60°方向上,前进100米到达B处,又测得航标C在北偏东45°方向上,如图9,在以航标C为圆心,120米长为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险?A、B两市相距100公里,在A市东偏北30 方向,B市的西北方向是一森林公园C,方圆30公里。若在A、B两市间修一条笔直的高速公路。它会不会穿过森林公园。1.这节课我的收获和疑问:___________________________我将__________________________________________________________解决我的困惑。2.解直角三角形的应用的常见类型有__________________________________________________________________________________________________________ 做一做,看谁做得快组内探索,交流推荐学生回答找生板书解答过程组内探索、讨论然后推举学生讲解思考回答、推举同学讲解先独立解答,不会的相互帮助所思所想
A
B
E
C
D
水平线
视线
视线
仰角
俯角
450
300
6米
A
C
D
B
B
C
10米
A
D
E
5.6米
i=1:2.5
α
β
A
E
F
D
C
B
A
B
D1
C1
A1
D
C
α
β
400
500
教学目标 理解仰角、俯角的意义,准确运用这些概念来解决一些实际问题。培养学生将实际问题抽象成数学模型并进行解释与应用的能力。在探究学习过程中,注重培养学生的合作交流意识,激发学生学习数学的兴趣。
教学重点 理解仰角和俯角的概念。
教学难点 能解与直角三角形有关的实际问题。
第一课时
教学过程 教师活动 学生活动
一、课前延伸二、课内探究三、精讲例题四、巩固练习五、拓展延伸 1、仰角和俯角在实际测量时,从低处观测高出的目标时,( )与( )所成的锐角叫做仰角;从高出观测低处的目标时,( )与( ) 所成的锐角叫做俯角。2、解决直角三角形的应用思路。(1)把实际问题转化为解直角三角形的问题,关键是找出实际问题中的 ( ),直角三角形( )之间的关系,是解决与直角三角形有关的实际问题的重要工具。(2)解答过程的思路:1、创设问题情景,引出新知:上海东方明珠塔于1994 年10 月1 日建成,出示图片,在各国广播电视塔的排名榜中,当时其高度列亚洲第一、世界第三。与外滩的“万国建筑博览群”隔江相望。在塔顶俯瞰上海风景,美不胜收。运用本章所学过的知识,能测出东方明珠塔的高度来吗?2、探究新知:(1)认识仰角与俯角:想要解决刚才的问题,我们先来了解仰角、俯角的概念,利用多媒体演示仰角、俯角。(2)引导学生小组探究解决导入中提出的问题。为了测量东方明珠塔的高度,同学们在距离东方明珠塔200 米处的地面上,用高1.20 米的测角仪测得东方明珠塔顶的仰角为60°48 ′。根据测量的结果,小亮画了一张示意图,其中 ( ) 表示东方明珠塔,( ) 为测角仪的支架,DC= ( )米,CB= ( )米,∠ADE= ( )。根据在前一学段学过的长方形对边相等的有关知识,你能求出AB 的长吗?例1如图,厂房屋顶人字架的跨度为10米,上弦AB=BD,∠A=260,求中柱BC和上弦AB的长(精确到0.01米)例2如图,某直升飞机执行海上搜救任务,在空中A出观测到海面上有一目标B,俯角是α=18°23′,这时飞机的高度为1500米,求飞机A与目标B的水平距离。练习1 如图,在电线杆上离地面6 米处用拉线固定电线杆,拉线和地面之间的夹角为60°,求拉线AC 的长和拉线下端点A 与线杆底部D 的距离(精确到0 .1 米)。 练习2两座建筑AB及CD,其地面距离AC为50.4米,从AB的顶点B测得CD的顶部D的仰角β=250,测得其底部C的俯角α=50°,求两座建筑物AB及CD的高。你还有那些方法测量物体的高度?(1)这节课你学到了什么?你有何体会?(2)这节课你还存在什么问题? 思考回答思考回答思考回答各小组讨论,互动完成解题过程。独立思考,自己解决畅所欲言,总结所学所得
第二课时
教学目标 1.学会解直角三角形在实际问题中的应用; 2.提高学生观察、分析、综合解决问题的能力。3.增强学生创新意识,培养学生学习能力;体验数学在实际生活中的应用;渗透理论联系实际的辩证唯物主义思想。
教学重点 解直角三角形在测量方面的应用。
教学难点 综合应用知识程度较高的例3.
教学过程 教师活动 学生活动
一、复习提问,加深理解二、提出问题,引入新课三、给出问题,共同探究四、思维扩展,举一反三五、巩固提高 六、扩展延伸,再进一步 1.直角三角形共有几个元素构成?它们分别是什么?2.什么是解直角三角形?3.如何解直角三角形呢?三边关系:两锐角的关系:边角关系: 我们在生活中,观看一个较高的物体需要抬起头来往上看,用一个词语来描述叫做什么?(仰视)那低下头看一个物体又怎么描述呢?(俯视)那么,我们来看一下这个分析图: 仰角:俯角:例1热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120m,你能算出楼的高度吗?引导提示:1.你能不能把它抽象成数学问题?2.看一下其中的图形是什么形状?3.根据已知条件和所学知识,这种形状的图形能不能解?仿照例1根据下图和图中的已知,编写一道应用“解直角三角形”知识的题。(要求叙述完整)例2如图,河对岸有水塔AB.在C处测得塔顶A的仰角为30°,向塔前进12m到达D,在D处测得A的仰角为45°,求塔高。 引导:AB同时属于哪两个三角形?这两个三角形又已知了什么条件呢?是否可用这两个条件来表示出其它的边呢?如何表示?CD和CB有什么关系呢?现在你能列出一个方程来求AB了吗?如何列?请计算。BC—BD=CD ,CD=12 m,即AB/tg30°-AB/tg45°=12(不唯一)教师总结(1)利用解直角三角形解决实际问题。(2)测量问题中的两种模式。 积极思考、踊跃回答回答问题并学习新知识学生通过探索、发现问题关键所在,并列出算式通过编写题目来加深学生对解直角三角形应用的理解与掌握,达到扩散思维的作用1、积极思考,踊跃回答,并计算结果。2、四人小组讨论,给出结果。
第三课时
教学目标 1.明确方位角、坡角、坡度的概念,并能将之灵活应用于实际生活。2.能熟练运用解直角三角形的有关知识来解决实际应用问题。3.会解决底部不能到达的物件高度的测量问题。
教学重点 能熟练运用解直角三角形的有关知识来解决实际应用问题。
教学难点 底部不能到达的物件高度的测量问题。
教学过程 教师活动 学生活动
一、学前准备二、自学探究三、练习自测四、拓展延伸五、归纳小结 指南或指北的 方向与目标方向线构成小于900的角,叫做__ ____,如图:点A在点O的___________,点B在点O的南偏西45 或 方向。2阅读课本有关坡度的内容,说一说什么是坡角,什么是坡度或坡比,坡度与坡角的正切有什么关系? 请把重点知识写在下面。______________________________________________________________________________1.某地计划在河流的上游修建一条拦水大坝,大坝的横断面ABCD是梯形(如图),坝顶宽BC=6米,坝高25米,应水坡AB的坡度i=1:3,被水坡CD的坡度i=1:2.5.(1)求斜坡AB和CD的长(精确到0.01米);(2)。求拦水大坝的底面AD的宽。 2.要测量铁塔的高AB,在地面上选取一点C,在AC两点间选取一点D,测得CD=14米,在C,D两点处分别用测角仪测得铁塔顶端B的仰角为α=300和β=450. 测角仪支架的高为1.2米,求铁塔的高(精确到0.1米)3.如图,一船从A点出发,沿北偏东方向航行12海里到达B点,然后又沿南偏东方向航行16海里到达C点,那么从C点再航行多远才能直接返回出发点A(精确到0.1海里)1.一名滑雪运动员从坡度为1:5的山坡上滑下,如果这名运动员滑行的距离为150米,那么他下降的高度是多少(精确到0.1米)?2.如上图,拦水坝的横断面为梯形ABCD,根据图中数据,求:(1)角α和β的大小(精确到 )(2)坝底宽AD和斜坡AB的长(精确到0.1米)3.入夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位,一条船在松花江某水段自西向东沿直线航行,在A处测得航标C在北偏东60°方向上,前进100米到达B处,又测得航标C在北偏东45°方向上,如图9,在以航标C为圆心,120米长为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险?A、B两市相距100公里,在A市东偏北30 方向,B市的西北方向是一森林公园C,方圆30公里。若在A、B两市间修一条笔直的高速公路。它会不会穿过森林公园。1.这节课我的收获和疑问:___________________________我将__________________________________________________________解决我的困惑。2.解直角三角形的应用的常见类型有__________________________________________________________________________________________________________ 做一做,看谁做得快组内探索,交流推荐学生回答找生板书解答过程组内探索、讨论然后推举学生讲解思考回答、推举同学讲解先独立解答,不会的相互帮助所思所想
A
B
E
C
D
水平线
视线
视线
仰角
俯角
450
300
6米
A
C
D
B
B
C
10米
A
D
E
5.6米
i=1:2.5
α
β
A
E
F
D
C
B
A
B
D1
C1
A1
D
C
α
β
400
500
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
