14.3.2公式法 (第1课时) 课件(20张ppt)
文档属性
| 名称 | 14.3.2公式法 (第1课时) 课件(20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
14.3.2公式法(第1课时)
人教版 八年级上册
教学目标
【教学目标】
1.探索并运用平方差公式进行因式分解,体会转化思想.(重点)
2.能会综合运用提公因式法和平方差公式对多项式进行因式分解.(难点)
回顾复习
1.什么叫把多项式分解因式
把一个多项式化成几个整式的积的形式,叫做多项式的分解因式.
2.已学过哪一种分解因式的方法
提公因式法
新知探究
想一想:多项式a2-b2有什么特点?你能将它分解因式吗?
是a,b两数的平方差的形式
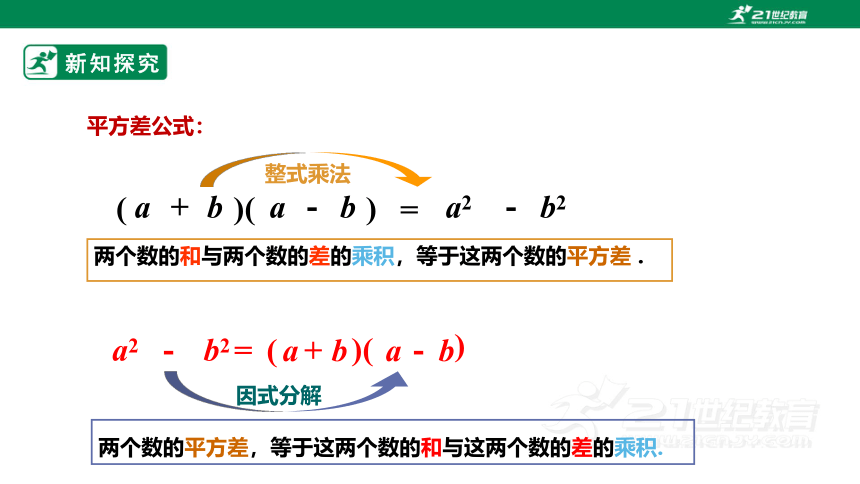
平方差公式:
(a+b)(a-b)=a2-b2
整式乘法
因式分解
这种分解因式的方法称为公式法.
a2-b2= (a+b)(a-b)
新知探究
)
)(
(
b
a
b
a
-
+
=
b2
a2
-
)
)(
(
b
a
b
a
b2
a2
-
+
=
-
整式乘法
因式分解
两个数的和与两个数的差的乘积,等于这两个数的平方差 .
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
平方差公式:
新知探究
公式左边:
1
多项式有两项;
2
这两项异号;
3
两项是平方差.
公式右边:
两个数的和与这两个数的差的乘积的形式.
因式分解平方差公式:
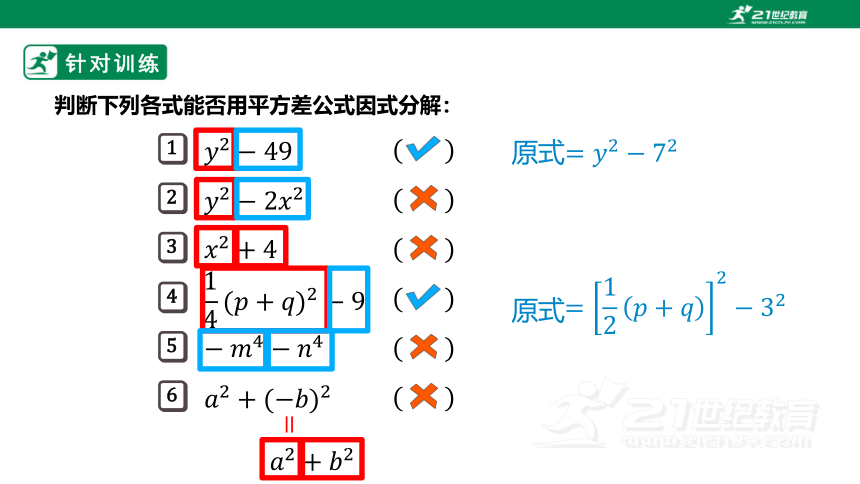
针对训练
1
2
3
判断下列各式能否用平方差公式因式分解:
4
5
6
原式
原式
新知探究
例3 分解因式:
(1)4x2 - 9;
(2) (x + p)2 -(x + q) 2.
分析:在(1)中, 4x2 = (2 x) 2 , 9 = 3 2, 4 x2 - 9 =
(2 x) 2 -3 2 ,即可用平方 差公式分解因式;
在(2)中,把x + p和x + q各看成一个整体,设x + p = m, x + q = n ,则原式化为m 2 - n 2.
新知探究
解:(1) 4x2 - 9
=(2 x )2 - 3 2
= (2x + 3)(2x - 3);
(2) (x + p)2 -(x + q) 2
= [( x + p) + (x + q)][(x + p ) - (x + q) ]
= (2x + p + q)(p - q).
“两项、异号、平方形式”是避免错用平方差
公式的有效方法.
新知探究
例4 分解因式:
解:(1)原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
分解因式后,一定要检查是否还有能继续分解的因式,若有,则需继续分解.
=(x2+y2)(x+y)(x-y);
(2)原式=ab(a2-1)
分解因式时,一般先用提公因式法进行分解,然后再用公式法.最后进行检查.
=ab(a+1)(a-1).
新知探究
用平方差公式分解因式时,若多项式有公因式,要先提取公因式,再用平方差公式分解因式.
平方差公式在分解因式中的应用:
课堂练习
1.下列多项式中能用平方差公式分解因式的是( )
A.a2+(-b)2 B.5m2-20mn
C.-x2-y2 D.-x2+9
D
2.若a+b=3,a-b=7,则b2-a2的值为( )
A.-21 B.21 C.-10 D.10
A
3.一次课堂练习,小颖同学做了以下几道因式分解题,你认为她做得不够完整的是( )
A.x3-x=x(x2-1)
B.x2y-y3=y(x+y)(x-y)
C.-m2+4n2=(2n+m)(2n-m)
D.3p2-27q2=3(p+3q)(p-3q)
课堂练习
A
课堂练习
4.把下列各式分解因式:
x2-4=______________.
a2-4b2=______________.
a3-a=______________.
9xy3-36x3y=_________________;
(x+2)(x-2)
(a+2b)(a-2b)
a(a+1)(a-1)
9xy(y+2x)(y-2x)
5.若将(2x)n-81分解成(4x2+9)(2x+3)(2x-3),则n的值是_____________.
4
课堂练习
6.已知4m+n=40,2m-3n=5.求(m+2n)2-(3m-n)2的值.
原式=-40×5=-200.
解:原式=(m+2n+3m-n)(m+2n-3m+n)
=(4m+n)(3n-2m)
=-(4m+n)(2m-3n),
当4m+n=40,2m-3n=5时,
课堂练习
7.如图,在边长为6.8 cm正方形钢板上,挖去4个边长为1.6 cm的小正方形,求剩余部分的面积.
解:根据题意,得
6.82-4×1.62
=6.82- (2×1.6)2
=6.82-3.22
=(6.8+3.2)(6.8 - 3.2)
=10×3.6
=36 (cm2)
答:剩余部分的面积为36 cm2.
课堂小结
1.利用平方差公式分解因式:
1
多项式有两项;
2
这两项异号;
3
两项是平方差.
两个数的和与这两个数的差的乘积.
注意:字母公式中的字母 , 可以表示数、单项式或多项式.
课堂小结
2.利用平方差公式分解因式步骤:
1
若多项式中有公因式,应先提取公因式,再进一步分解因式;
2
剩余因式若有两项,异号,两项是平方差,则用平方差公式继续分解因式.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.3.2公式法(第1课时)
人教版 八年级上册
教学目标
【教学目标】
1.探索并运用平方差公式进行因式分解,体会转化思想.(重点)
2.能会综合运用提公因式法和平方差公式对多项式进行因式分解.(难点)
回顾复习
1.什么叫把多项式分解因式
把一个多项式化成几个整式的积的形式,叫做多项式的分解因式.
2.已学过哪一种分解因式的方法
提公因式法
新知探究
想一想:多项式a2-b2有什么特点?你能将它分解因式吗?
是a,b两数的平方差的形式
平方差公式:
(a+b)(a-b)=a2-b2
整式乘法
因式分解
这种分解因式的方法称为公式法.
a2-b2= (a+b)(a-b)
新知探究
)
)(
(
b
a
b
a
-
+
=
b2
a2
-
)
)(
(
b
a
b
a
b2
a2
-
+
=
-
整式乘法
因式分解
两个数的和与两个数的差的乘积,等于这两个数的平方差 .
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
平方差公式:
新知探究
公式左边:
1
多项式有两项;
2
这两项异号;
3
两项是平方差.
公式右边:
两个数的和与这两个数的差的乘积的形式.
因式分解平方差公式:
针对训练
1
2
3
判断下列各式能否用平方差公式因式分解:
4
5
6
原式
原式
新知探究
例3 分解因式:
(1)4x2 - 9;
(2) (x + p)2 -(x + q) 2.
分析:在(1)中, 4x2 = (2 x) 2 , 9 = 3 2, 4 x2 - 9 =
(2 x) 2 -3 2 ,即可用平方 差公式分解因式;
在(2)中,把x + p和x + q各看成一个整体,设x + p = m, x + q = n ,则原式化为m 2 - n 2.
新知探究
解:(1) 4x2 - 9
=(2 x )2 - 3 2
= (2x + 3)(2x - 3);
(2) (x + p)2 -(x + q) 2
= [( x + p) + (x + q)][(x + p ) - (x + q) ]
= (2x + p + q)(p - q).
“两项、异号、平方形式”是避免错用平方差
公式的有效方法.
新知探究
例4 分解因式:
解:(1)原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
分解因式后,一定要检查是否还有能继续分解的因式,若有,则需继续分解.
=(x2+y2)(x+y)(x-y);
(2)原式=ab(a2-1)
分解因式时,一般先用提公因式法进行分解,然后再用公式法.最后进行检查.
=ab(a+1)(a-1).
新知探究
用平方差公式分解因式时,若多项式有公因式,要先提取公因式,再用平方差公式分解因式.
平方差公式在分解因式中的应用:
课堂练习
1.下列多项式中能用平方差公式分解因式的是( )
A.a2+(-b)2 B.5m2-20mn
C.-x2-y2 D.-x2+9
D
2.若a+b=3,a-b=7,则b2-a2的值为( )
A.-21 B.21 C.-10 D.10
A
3.一次课堂练习,小颖同学做了以下几道因式分解题,你认为她做得不够完整的是( )
A.x3-x=x(x2-1)
B.x2y-y3=y(x+y)(x-y)
C.-m2+4n2=(2n+m)(2n-m)
D.3p2-27q2=3(p+3q)(p-3q)
课堂练习
A
课堂练习
4.把下列各式分解因式:
x2-4=______________.
a2-4b2=______________.
a3-a=______________.
9xy3-36x3y=_________________;
(x+2)(x-2)
(a+2b)(a-2b)
a(a+1)(a-1)
9xy(y+2x)(y-2x)
5.若将(2x)n-81分解成(4x2+9)(2x+3)(2x-3),则n的值是_____________.
4
课堂练习
6.已知4m+n=40,2m-3n=5.求(m+2n)2-(3m-n)2的值.
原式=-40×5=-200.
解:原式=(m+2n+3m-n)(m+2n-3m+n)
=(4m+n)(3n-2m)
=-(4m+n)(2m-3n),
当4m+n=40,2m-3n=5时,
课堂练习
7.如图,在边长为6.8 cm正方形钢板上,挖去4个边长为1.6 cm的小正方形,求剩余部分的面积.
解:根据题意,得
6.82-4×1.62
=6.82- (2×1.6)2
=6.82-3.22
=(6.8+3.2)(6.8 - 3.2)
=10×3.6
=36 (cm2)
答:剩余部分的面积为36 cm2.
课堂小结
1.利用平方差公式分解因式:
1
多项式有两项;
2
这两项异号;
3
两项是平方差.
两个数的和与这两个数的差的乘积.
注意:字母公式中的字母 , 可以表示数、单项式或多项式.
课堂小结
2.利用平方差公式分解因式步骤:
1
若多项式中有公因式,应先提取公因式,再进一步分解因式;
2
剩余因式若有两项,异号,两项是平方差,则用平方差公式继续分解因式.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
